第三章——非线性规划的数学模型
前言
非线性规划比线性规划更困难,没有统一的数学模型,有自己特定的适用范围,目前还没有通用于所有问题的非线性规划问题的算法
一、 数学模型

满足以上条件的解释可行解,所有解为可行域,如果可行域=Rn,则为无约束问题,否则为有约束问题
如果所有的约束与目标函数都是凸函数,则成为凸规划问题,凸规划问题的解可以简单判定为是否是全局最优解
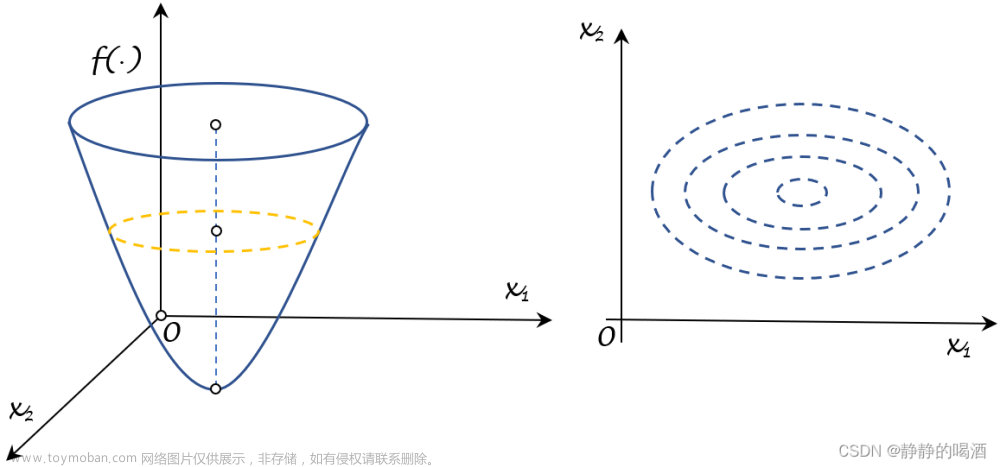
二、 直观理解

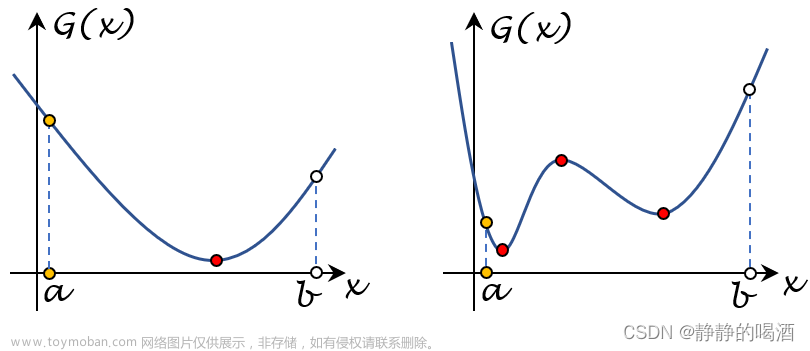
局部最优解:在一个小邻域内的最优解
全局最优解:整个定义域内的最优解
线性规划LP问题有最优解,最优解必可以在极点上达到
非线性规划NLP问题的最优解可能是可行域上的任一点,且有局部和全局最优解之分,并且一般求出的都是局部最优解,对于凸规划则局部最优是全局最优
三、无约束问题的最优性条件
导数、梯度、极值、法向量
梯度就是过点X0等值线在该点处的法向量\法平面等
Hessian矩阵:就是二阶导矩阵
多元函数的泰勒展开——》线性逼近和二次逼近
局部极值点的必要条件:
局部极值点的充分条件:
最优解需要满足的必要条件:
(如果不满足梯度=0,那么肯定还可以走向更小的防线)
一阶必要条件
二阶必要条件:
最优解的充分条件:


二次终止性:算法应用于一个二次函数,只要经过有限步的迭代就一定能达到函数的极小值点
例题:
这里的Hessian矩阵有打错,是把X1到X4全带入得到的四个矩阵
四、 凸的无约束问题的最优性条件
凸函数的一阶充要条件:
凸函数的二阶充要条件:
凸函数的局部极小点就是全局的极小点
所以定义在凸集上的凸函数极值点有很好的的性质,应用到非线性规划问题上,相当于目标函数和约束都是凸函数,可行域是突击的规划问题成为凸规划问题。
如何判断可行域:

五、基本思路
最优化方法通常采用迭代方法(iterative)求解
基本思想:给定一个初始点x(0)∈Rn,按照某种迭代规则(一般称为算法)产生一个点{x(k)},使得当{x(k)}是有穷点列时,其最后一个点是最优化模型问题的最优解;当{x(k)}是无穷点列时,它有极限点,且其极限点是最优化模型问题的最优解
最优化方法的基本结构,给定初始点x^(0)
1.确定搜索方向p(k):即依照一定的准则,构造f在x(k)点处的下降方向作为搜索方向
2.确定步长因子λ_k,使目标函数值有某种意义的下降
3.令x(k+1)=x(k)+λ_kp(k),若x(k+1)满足某种终止条件,则停止迭代,得到近似最优解x(k+1),否则,重复以上步骤
下降方向:
是指对目标函数f:Rn→R1,x ̅∈Rn,向量p∈Rn(p≠0),若存在δ>0,∀λ∈(0,δ),都有f(x ̅+λp)<f(x ̅),则称向量p为函数在x ̅的下降方向
凡满足这种迭代性质的最优化方法都可称为下降方法(Descent methods)
可行下降方向:
对于有约束的非线性规划问题, min f(x), x∈ℵ,不仅要求下降,而且x(k+1)必须仍然在原问题的可行域内,此时称为可行下降方向
一维搜索的最优步长λ_k,所对应的点x(k+1)处的目标函数的梯度∇f(x(k+1))与搜索方向p(k)正交
计算的终止条件(Termination criterion)与收敛速度(Convergence rate)


 文章来源:https://www.toymoban.com/news/detail-437102.html
文章来源:https://www.toymoban.com/news/detail-437102.html
二次终止性
一个算法用于解正定二次函数的无约束极小时,有限步迭代可达最优解,则称该算法具有二次终结性。
二次终结性=共轭方向+精确一维搜索

 文章来源地址https://www.toymoban.com/news/detail-437102.html
文章来源地址https://www.toymoban.com/news/detail-437102.html
注:47页之后的没有看
到了这里,关于最优化学习笔记——第三章的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!




![《现代密码学》学习笔记——第三章 分组密码 [二] AES](https://imgs.yssmx.com/Uploads/2024/02/447027-1.png)




