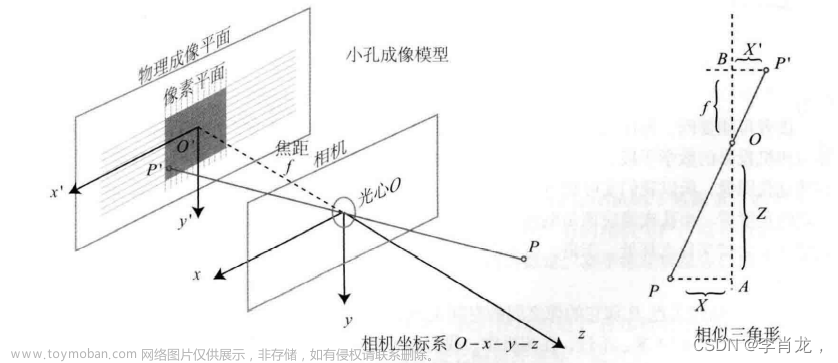
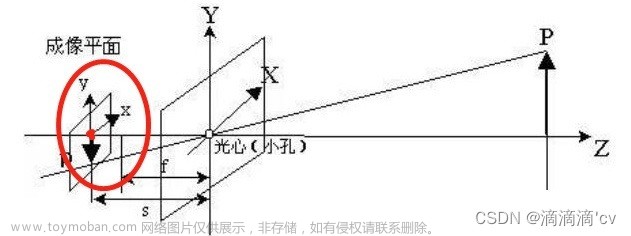
最近系统性学习了一遍LIO-SAM,开始的时候一直搞不懂里程计坐标系,经过不断学习才有了一点自己的拙见。
引言:首先我们搞清楚SLAM算法主要是解决建图与定位问题,其更侧重定位,即让机器人知道自己在全局地图的哪个位置,只有这样才能继续后续的预测、感知、控制等模块。但是 SLAM算法做定位 这件事存在的意义就是为了解决当GPS这类非自主定位传感器信号不连续时的定位问题。SLAM算法主要是靠激光雷达/相机、IMU等传感器来做定位,但是不管是精度再高的激光雷达通过点云匹配得出位姿还是IMU预积分给出的位姿都会和map中的绝对位姿产生不断变化的误差,这个不断变化的误差便造就了不断变化的“里程计坐标系”。
继续往下看:
1.地图坐标系(map)
地图坐标系就是全局坐标系,其原点就是机器人刚开始出现在地图的那一点,属于固定坐标系,是不会动的。
2.里程计坐标系(odom)
这一部分是我想讲的重点,我会尽量讲详细,方便大家理解。
首先我们通过引言知道,里程计坐标系的产生是由于传感器的误差。举个例子:假设机器人在激光雷达第n帧走到了A点,A点在map上的坐标为(2,0),但是由于传感器的误差,导致传感器解算出来的坐标在(3,0),这个时候在odom下的坐标就是(3,0),因此可以说,odom相对于map在x方向上漂移了1m,如下图:

黑色代表odom,蓝色代表map。但是此时上图中的odom只存在于激光雷达第n帧的范畴内,假设到了激光雷达第n+1帧的时候,机器人走到了B点,B点在map上的坐标为(2,1),但是再次由于传感器的误差,导致传感器解算出来的坐标在(3,2),这个时候在odom下的坐标就是(3,2),因此可以说,odom相对于map在x方向上漂移了1m,y方向上漂移了1m,此时的odom与第n帧的odom就不同了,如下图

我们知道map坐标系是固定的,所以我们可以得到一个结论:odom是会随着每一帧激光雷达帧的输入而变化的。
我们回过头来看引言,SLAM算法做定位 这件事存在的意义就是为了解决当GPS这类传感器信号不连续时的定位问题,因此通过算法得出来的定位结果,本就不是绝对位姿,是一个通过解算估计出来的位姿,结合上面的图来说,我们通过SLAM算法得到的定位结果是B’而不是B(B是理想情况下的绝对位姿),但是我们最终需要得到的定位结果是在map坐标系下的位姿而不是odom下的。因此我们需要做一步操作,令每一帧的odom与map重合,即下图这样:

上图意思就是:机器人通过传感器解算得到的坐标在map中为(3,2),但是机器人实际在map中的绝对位置为(2,1)(这里不要理解错了,在地图中机器人是在(2,1)这个点的,B’这个点是传感器解算出来的,实际在地图中(3,2)这个点是没有机器人的,举个栗子,我(机器人)在家门口蒙着眼往家里面走,走了十步,我凭我自己在家里生活了这么多年的经验(传感器1)再加上我耳朵(传感器2)听到电视机的声音大小判断出来我这个时候在客厅并且距离电视机还有一米的距离(传感器结算出来的定位结果),但是我妈妈告诉我其实距离电视机还有两米的距离(绝对位置),这里的一米就相当于传感器解算的位置,妈妈告诉我的两米是绝对位置,因此我这个时候真正的位置是距离电视机两米的那个地方,而距离电视机只有一米的那个地方是没有人的,现在回到B点和B’点,机器人实际位置是在B点那个地方,B’这个点是没有机器人的。)算法解算位置与绝对位置在x与y方向有1的误差。(当然在实际的SLAM算法中的误差并没有这么大,只是为了方便大家理解,公司项目上就是用的LIOSAM这套代码,如果定位有1m的误差早把人撞si了哈哈哈)
OK现在回过头来看上面那个结论:我说odom是会随着每一帧而变化的,现在可能大家会问,odom与map重合以后不是固定了吗?我直接说答案,其实还是在变的,在坐标系重合之前,odom就是通过map中的绝对坐标与算法解算出来的坐标的误差创造出来的,只不过变化是相对的,现在坐标系虽说固定了,但是算法解算出来的坐标与实际坐标的误差是在不断变化的,因此可以理解为odom还是在不断变化的,只不过是看上去不变了。
总结:一句话概括,odom就是一个由于实际坐标与解算坐标两者的误差而产生的一个不断变化的坐标系。
3.基座坐标系(base_link)
这个就是机器人自身的坐标系,固定在机器人身上的某个位置,没啥好说的。
4.激光坐标系(laser_link)
这个就是激光雷达的坐标系,这个坐标系也很重要,对点云的操作(例如点云去畸变、提取特征点等等)就是在这个坐标系下完成的,也是固定在机器人身上的某个位置,与base_link的转换是固定的,甚至有些框架中base_link与laser_link是重合的,也没啥好说的。
到这里坐标系的部分就讲完了。我发这篇博客的目的,首先还是为了写一些有关SLAM坐标系的个人理解,如果能帮到大家也是我的荣幸;其次就是如果我哪里写错了,大家能纠正出来的话对我个人也有帮助,也欢迎大家积极留言评论。文章来源:https://www.toymoban.com/news/detail-437209.html
码字不易,感谢大家!文章来源地址https://www.toymoban.com/news/detail-437209.html
到了这里,关于对于SLAM定位中各类坐标系的理解(坐标系,里程计坐标系,基座坐标系与雷达坐标系)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!