【矩阵论】4. 矩阵运算——广义逆—

这篇具有很好参考价值的文章主要介绍了【矩阵论】4. 矩阵运算——广义逆——减号逆。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

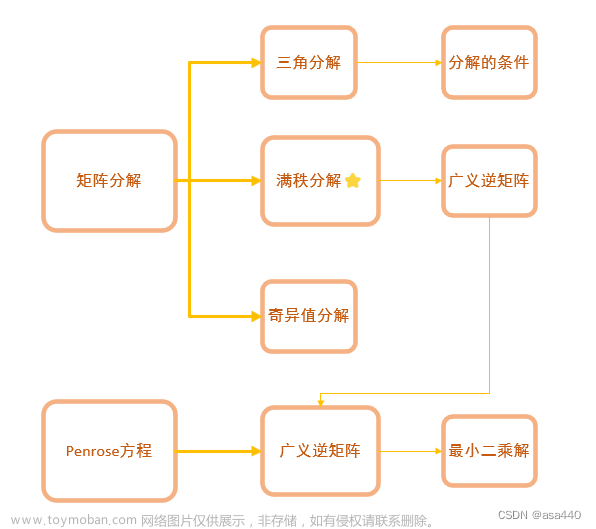
矩阵论的所有文章，主要内容参考北航赵迪老师的课件

[注]由于矩阵论对计算机比较重要，所以选修了这门课，但不是专业搞数学的，所以存在很多口语化描述，而且对很多东西理解不是很正确与透彻，欢迎大家指正。我可能间歇性忙，但有空一定会回复修改的。

矩阵论
1. 准备知识——复数域上矩阵,Hermite变换
1.准备知识——复数域上的内积域正交阵
1.准备知识——Hermite阵，二次型，矩阵合同，正定阵，幂0阵，幂等阵，矩阵的秩
2. 矩阵分解——SVD准备知识——奇异值
2. 矩阵分解——SVD
2. 矩阵分解——QR分解
2. 矩阵分解——正定阵分解
2. 矩阵分解——单阵谱分解
2. 矩阵分解——正规分解——正规阵
2. 矩阵分解——正规谱分解
2. 矩阵分解——高低分解
3. 矩阵函数——常见解析函数
3. 矩阵函数——谱公式,幂0与泰勒计算矩阵函数
3. 矩阵函数——矩阵函数求导
4. 矩阵运算——观察法求矩阵特征值特征向量
4. 矩阵运算——张量积
4. 矩阵运算——矩阵拉直
4.矩阵运算——广义逆——加号逆定义性质与特殊矩阵的加号逆
4. 矩阵运算——广义逆——加号逆的计算
4. 矩阵运算——广义逆——加号逆应用
4. 矩阵运算——广义逆——减号逆
5. 线性空间与线性变换——线性空间
5. 线性空间与线性变换——生成子空间
5. 线性空间与线性变换——线性映射与自然基分解,线性变换
6. 正规方程与矩阵方程求解
7. 范数理论——基本概念——向量范数与矩阵范数
7.范数理论——基本概念——矩阵范数生成向量范数&谱范不等式
7. 矩阵理论——算子范数
7.范数理论——范数估计——许尔估计&谱估计
7. 范数理论——非负/正矩阵
8. 常用矩阵总结——秩1矩阵，优阵(单位正交阵)，Hermite阵
8. 常用矩阵总结——镜面阵，正定阵
8. 常用矩阵总结——单阵，正规阵，幂0阵，幂等阵，循环阵

【矩阵论】4. 矩阵运算——广义逆——减号逆

4.5 减号逆

若 $A=A_{m\times n}$ 与 $X=X_{n\times m}$ ，有 $A X A = A$ ，则称 $X=X_{n\times m}$ 为A的减号逆(一号逆)，记为 $X=A^{-}=A^{(1)}$

全体 $A^{-}$ 的集合记为 $A^{\{1\}}=\{X\mid AXA=A\}$

$A^{-}\in A^{\{1\}}$

4.5.1 性质

a. 自反性

$AA^{-}A=A$

b. $A^-A$ 为幂等阵

$A^{-}A)^2=A^{-}A$ ， $AA^{-})^2=AA^{-}$
$证明：\because (A^-A)^2=A^-AA^-A=A^-A\Rightarrow A^-A为幂等阵$

秩迹公式

$r(A)=r(A^-A)=r(AA^-)=tr(AA^-)=tr(A^-A)$
$\begin{aligned} 证明： &r(A^-A)\le r(A),且A=AA^-A\Rightarrow r(A)=r(AA^-A)\le r(A^-A)\le r(A)\\ &故r(A)=r(A^-A)，同理，r(AA^-)=r(A)\\ &A^2=A\overset{x^2=x}{\Longrightarrow} \lambda=1或0,且A为单阵 \Rightarrow A\sim\Lambda=\left(\begin{matrix}\left(\begin{matrix}1&&&\\&1&&\\&&\ddots&\\&&&1\end{matrix}\right)&&\\&0&\\&&\ddots\end{matrix}\right)\\ &\therefore tr(A)=r(A)=r(A^-A)=r(AA^-)=tr(AA^-)=tr(A^-A) \end{aligned}$

$I-A^-A)^2=I-A^-A$

$r(I-A^-A)=n-r(A^-A)=n-r(A)$
$r(I-AA^-)=r(A)$

c. $A^{-}$ 不唯一

如 $A=\left(\begin{matrix}1\\0\end{matrix}\right)$ ，可取 X=(1 0) 或 Y=(1 1) 作为A的减号逆
$A^{-}$ 唯一的阵：方阵 $A_{n\times n}$ 可逆，则必有唯一 $A^{-1}=A^{+}=A^-$

d. 满秩乘积为单位阵

若 $A=A_{m\times n}$ 为列满秩（高阵），则 $A^-A=I_n$ ；若 $A$ 为行满秩（低阵），则 $AA^-=I_m$

【矩阵论】4. 矩阵运算——广义逆——减号逆

4.5.2 计算

a. 求解 $A X A = A$

求解减号逆 $A{-}$ 即求解 $A X A = A$ 的全体通解

【矩阵论】4. 矩阵运算——广义逆——减号逆在这里插入图片描述

$\begin{aligned} &由矩阵方程AXB=D的特解X_0=A^+=\left(1,0,0\right),故通解为A^-=X=X_0+Y-A^+AYAA^+\\ &=\left(1，0，0\right)+\left(\begin{matrix}a，b，c\end{matrix}\right)-\left(\begin{matrix}a，0，0\end{matrix}\right)=\left(\begin{matrix}1，b，c\end{matrix}\right) \end{aligned}$

也可见 $A^-$ 不唯一

对于高阶阵 $A^-=A^++(Y-A^+AYAA^+)$ 的计算比较复杂

b. 标准对角形

若 $A=\left(\begin{matrix}I_r&0\\0&0\end{matrix}\right)_{m\times n}$ ，则全体 $A^-=\left(\begin{matrix}I_r&B\\C&D\end{matrix}\right)_{n\times m}$ ，BCD为任一小块

【矩阵论】4. 矩阵运算——广义逆——减号逆

若 $PAQ=\left(\begin{matrix}I_r&0\\0&0\end{matrix}\right)_{m\times n}$ ，全体 $A^{-}=Q\left(\begin{matrix}I_r&B\\C&D\end{matrix}\right)_{n\times m}P$ ，BCD为任一小块

c. 初等行，列变换（一般方法）

设 $A=A_{m\times n}$ ，令 $\left(\begin{array}{c:c}A&I_m\\\hdashline I_n&0\end{array}\right)\xrightarrow[列变换]{行变换}\left(\begin{array}{c:c}\left(\begin{matrix}I_r&0\\0&0\end{matrix}\right)_{m\times n}&P\\\hdashline Q&0\end{array}\right)$ ，则有 $A^-=Q\left(\begin{matrix}I_r&B\\C&D\end{matrix}\right)_{n\times m}P$