[一、什么是算法]
算法(英文algorithm)这个词在中文里面博大精深,表示算账的方法,也可以表示运筹帷幄的计谋等。在计算机科技里,它表示什么呢?
计算机,顾名思义是用来计算的机器。算法在计算机科学中可以描述为:计算机接收一个输入指令,然后进行一个过程处理,最后输出计算的结果。
这种输入-过程处理-输出,用人类的行为模式,很容易理解,比如妈妈让小明去打酱油,打酱油的命令是输入,小明发现小区周边有5家店有酱油出售,娟娟超市是离家最近的,而子龙杂货店虽然离得最远,但酱油很便宜。小明为了省钱,跑到最远的子龙杂货店买了酱油,然后顺利回到了家,交给了妈妈。买酱油的过程就是处理,而给妈妈的酱油是输出。
小明为什么不去最近的娟娟超市,而去了最远的子龙杂货店,这是小明脑袋里思考后产生的最佳方案。当然,现在买酱油可以通过外卖软件,小明可以打开美团外卖软件,搜索关键字:酱油,然后点击筛选,离家最近的和最便宜的,然后选择最便宜的酱油下单。
买酱油的过程 = 美团外卖软件下单的过程。
人类在几千年的演化中,会进行数字运算了,会进行利益权衡了,然后造了机器,将自己的行为模式,赋予了机器,解放了自身。如果人类真正了解人脑神经元的信息传递过程,甚至可能造出有自我意识的机器,但这种场景仍然只能在科幻电影中看到。
所以,这个逻辑过程,或行为模式,在计算机里面映射的是算法。
用更准确的描述来说:算法是一种有限,确定,有效的并适合用计算机程序来实现的,用来解决问题的方法。首先,有一个问题,然后有一个方法去解决它,这个方法叫算法。
算法是有限的,就是算法的步骤是有限的,执行的时间也是有限的,能够在有限时间内得出结果。算法是确定的,就是无论执行多少次,计算得出的结果都一样。算法是有效的,就是计算出的结果对解决问题有帮助。
然而算法的定义一直被刷新,因为机器学习的出现,基于海量超大规模数据,机器学习算法的步骤是无限的,可以一直计算下去,每次计算的结果也不一样,但如果人为进行步骤限制,以及增加训练阈值,训练时得出的参数超过设定的阈值马上停止运算,倒也符合以上的定义。
算法要在有限的时间内完成,本身是对人类的一种负担,因为人类造出的机器还不够强。为什么呢?因为即使算法的步骤是有限的,执行的时间也可能特别长。
正如《从一到无穷大》书中印度教圣地贝拿勒斯神庙下的三根宝石针,印度教主神焚天说过,谁可以把第一根宝石针的64块金片通过第二根宝石针移到第三根,焚天塔,神庙,婆罗门将化为灰烬,这是有名的汉诺塔算法。
汉诺塔问题可以描述为:
有三根杆(编号 A、B、C),在 A 杆自下而上、由大到小按顺序放置 64 个金盘(如下图)。游戏的目标:把 A 杆上的金盘全部移到 C 杆上,并仍保持原有顺序叠好。

操作规则:每次只能移动一个盘子,并且在移动过程中三根杆上都始终保持大盘在下,小盘在上,操作过程中盘子可以置于 A、B、C 任一杆上。
我们很自然想到一个算法:
- 我们必须先借助
C杆,将A杆前面N-1个盘子,移动到B杆后,将A杆剩下的一个盘子,直接移动到C杆,这时候A空了。 - 然后借助
A杆,将B杆的N-1个盘子,移动到C杆,任务就完成了。
十分朴素的思路,我们用编程语言来实现:
package main
import "fmt"
var total = 0
// 汉诺塔
// 一开始A杆上有N个盘子,B和C杆都没有盘子。
func main() {
n := 4 // 64 个盘子
a := "a" // 杆子A
b := "b" // 杆子B
c := "c" // 杆子C
tower(n, a, b, c)
// 当 n=1 时,移动次数为 1
// 当 n=2 时,移动次数为 3
// 当 n=3 时,移动次数为 7
// 当 n=4 时,移动次数为 15
fmt.Println(total)
}
// 表示将N个盘子,从 a 杆,借助 b 杆移到 c 杆
func tower(n int, a, b, c string) {
if n == 1 {
total = total + 1
fmt.Println(a, "->", c)
return
}
tower(n-1, a, c, b)
total = total + 1
fmt.Println(a, "->", c)
tower(n-1, b, a, c)
}
Copy to clipboardErrorCopied
通过归纳,我们可以知道移动次数 Total(N) 的关系是 Total(N)=2*Total(N-1)+1,每多一个盘子,移动次数就会翻倍加一,我们通过相关的数列数学方法可以知道 Total(N)=2^N-1,也就是移动次数是一个指数方程:2的N次方,指数等于盘子的数量。
我们计算出 2^64-1=18446744073709551615,可以知道一个人日夜不停,一秒移动一次:18446744073709551615/3600/24/365/100000000=5849,要5849亿年时间才可以完成这件事,那时候世界确实可能已经毁灭。
在计算机科学中,因为所有的算法都是人定义的规则,规则是死的,所以不要担心学不会。当你学会了这些算法,你将会觉得,哇,一切都那么简单。
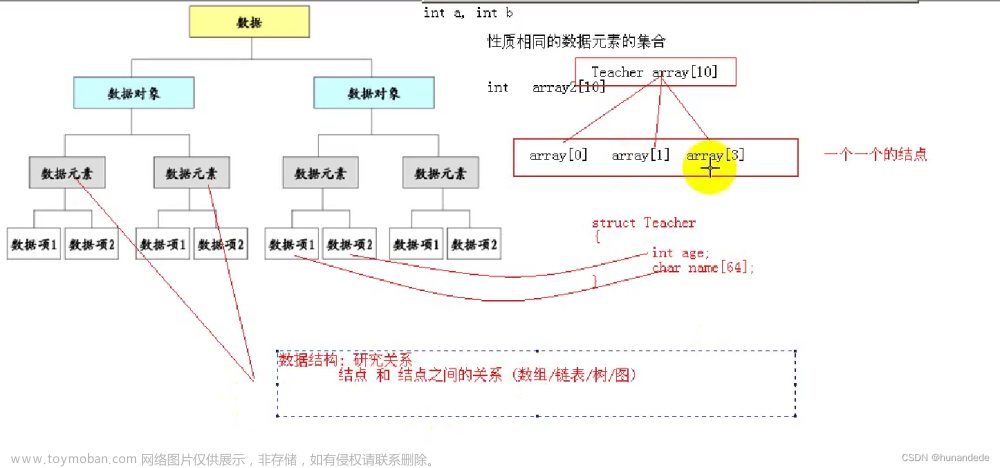
[二、什么是数据结构]
数据结构,顾名思义就是存放数据的结构,也可以认为是存放数据的容器。比如,你要找出1000个数字中的最大值,首先你要将1000个数字记在某些卡片上,然后对卡片进行排序。
大多数算法都需要组织数据,所以产生了数据结构。数据结构在计算机中,主要是用来实现各种算法的基础,当然数据结构本身也是算法的一部分。
基本的数据结构有:链表,栈和队列,树和图。
链表,就是把数据链接起来,关联起来,一个数据节点指向另外一个数据节点,像自然界的一条条铁链,大部分数据结构,都是由链表的若干变种来表示。
在每种编程语言中,数组作为基本数据类型提供,数组是连续的内存存储空间,通过下标0,1,2可以迅速获取到数组指定位置的数据。链表也可以用数组来实现,但一般情况下,因为数组是连续的,在链表增加和删除节点时容易造成冗余,效果不佳。所以链表在不同编程语言实现是这样的:
C、C++是用指针来实现的,Java是用类来实现的,而Golang是用结构体引用来实现。
栈和队列,主要用来存储多个数据,只不过一个是先进后出,一个先进先出。比如下压栈,先入栈的数据是最后才能出来,而我们熟知的队列,先排队的人肯定先获得服务。
其次是树和图,树就是有一个树根节点,存放着数据,下面有很多子节点,也存放着数据,类比自然界的树。图则可以类比自然界的地图,多个点指向多个点,点和点之间有一条或多条边,而这些点存放着数据,边也可以存放着数据,比如距离等。
围绕这几种数据结构,有若干延伸,加上一些排序,查找逻辑,就形成了更高层次的高级数据结构。
数据结构是算法实现的辅助,是为了更高效组织数据的结构,所以数据结构和算法其实密切联系,并不需要分得太清,大家可以把数据结构等同于算法。
[三、什么叫好的数据结构和好的算法]
学习算法的原因,是好的算法可以节约资源,但是选择合适的算法很难。我们要进行复杂的数学分析才能知道,什么叫做好的,在计算机里,我们把这种数学分析这叫做算法分析。
什么是好的数据结构和好的算法?
-
计算机资源是有限的,所以占用计算机资源越少的数据结构和算法越好。 -
人的生命是有限的的,等待时间是有忍耐度的,所以能辅助程序越快完成工作的数据结构和算法越好。
所以出了个理论:时间和空间算法复杂度理论。
程序执行过程中,要么空间换时间,要么时间换空间,空间可以认为是一种计算机资源如内存使用情况,而时间是人类感知的第四个维度,就是慢还是快,两者一般不能兼得,如果发现居然兼得了,那就是发明了一种更好的算法。
在计算机科学发展的四五十年,这种既省资源又省时间的发明还是比较少的,比如数据压缩算法,因为发明了超高效的无损数据压缩算法,我们网上看视频的时候,既不失真,也不卡顿,又快又好,这种就叫好算法。
目前有一种新型的计算方式正在研究中,叫量子计算,可以在非常小的空间,使用非常少的资源,短时间内计算超级大量的数据,让我们期待能成功量产的那天,到了那时候,人类生产力将极大被解放。
[四、总结]
程序设计在一般程度上,很多人都认为=数据结构+算法。
我们学习数据结构和算法,是为了更高效率写出更快,更好的代码。
因为学习过,所以我们不需要从零开始设计,工作效率就提高了。
因为知道每种数据结构和算法的复杂度和适用场景,自由选择组合,我们写出的代码计算速度变快了,占用的资源更少了。
所以我们要好好学习和理解常见的数据结构和算法。
一、算法复杂度
首先每个程序运行过程中,都要占用一定的计算机资源,比如内存,磁盘等,这些是空间,计算过程中需要判断,循环执行某些逻辑,周而反复,这些是时间。
那么一个算法有多好,多快,怎么衡量一个算法的好坏?所以,计算机科学在算法分析过程中,提出了算法复杂度理论,这套理论可以量化算法的效率,以此作为标准,方便我们能衡量到底选择哪一种算法。
复杂度有两个维度:时间和空间。
我们说,一个实现了某算法的程序:
- 如果计算的速度越快,那么这个算法时间复杂度越低。
- 如果占用的计算资源越少,那么空间复杂度越低。
我们要选择复杂度低的算法,衡量好空间和时间的消耗,选出适合特定场景的算法。
这两个复杂度维度的量化过程都是一样的,所以我们这里主要介绍时间复杂度。
如何进行算法描述呢?
二、算法规模
计算1+2+3+4+…+100,按照最方便的方法进行
func sum(n int)int{
total:=0
for i:=0;i<=n;i++{
total=total+i
}
return total
}
当 n = 10 时就等于我们要计算的公式。这个算法要循环 n-1 次,当 n 很小时,计算很快,但当 n 无限大的时候,计算很慢。
所以,算法衡量要衡量的是在不同 问题规模 n 下,算法的速度。
在这里,因为要循环计算 n-1 次,而当 n 无限大时,常数项基本忽略不计,所以这个算法的时间复杂度,我们用 O(n) 来表示。
当然我们还能想到利用数学公式来计算
func sum(n int)int{
total:=((1+n)*n)/2
return total
}
这次算法只需执行 1 次,所以这个算法的时间复杂度是 O(1)。可以看出,时间复杂度为 O(1) 的算法优于复杂度为 O(n) 的算法。
当然,还有指数级别的比如之前的汉诺塔算法,对数级别的,阶乘级别的复杂度,如 O(2^n),O(n!),O(logn) 等。
算法的优先级排列如下,一般排在上面的要优于排在下面的:
- 常数复杂度:
O(1) - 对数复杂度:
O(logn) - 一次方复杂度:
O(n) - 一次方乘对数复杂度:
O(nlogn) - 乘方复杂度:
O(n^2),O(n^3) - 指数复杂度:
O(2^n) - 阶乘复杂度:
O(n!) - 无限大指数复杂度:
O(n^n)
有想法的可以去了解以下几个渐进符号的含义:
如何量化一个复杂度,到底有多复杂,计算机科学抽象出了几个复杂度渐进符号。
渐进符号如下:
`O`,`ο`,`Θ`,`Ω`,`ω`
分别读作:Omicron(大欧),omicron(小欧),Theta(西塔),Omega(大欧米伽),omega(小欧米伽)。
3、补充 延伸-计算理论:P和NP问题
在计算机科学中,有一个专门的分支研究问题的可计算性,叫做计算理论。
我们用计算机算法来解决一个问题,如果一个问题被证明很难计算,或者只能暴力枚举来解决,那么我们就不必花大力气去质疑使用的算法是不是错了,为什么这么慢,计算怎么久都没出结果,到底有没有更好的算法。
计算机科学把一个待解决的问题分类为:P 问题,NP 问题,NPC 问题,NP-hard 问题。
一、P 和 NP 问题
类似于 O(1),O(logn),O(n) 等复杂度,规模 n 出现在底数的位置,计算机能在多项式时间解决,我们称为多项式级的复杂。
类似于 O(n!),O(2^n) 等复杂度,规模 n 出现在顶部的位置,计算机能在非多项式时间解决,我们称为非多项式级的复杂度。
如果一个问题,可以用一个算法在多项式时间内解决,它称为 P 问题(P 为 Polynominal 的缩写,多项式)。
比如求1加到100的总和,它的时间复杂度是 O(n),是多项式时间。
然而有些问题,只能用枚举的方式求解,时间复杂度是指数级别,非多项式时间,但是只要有一个解,我们能在多项式时间验证这个解是对的,这类问题称为 NP 问题。
也就是说,如果我们只能靠猜出问题的一个解,然后可以用多项式时间来验证这个解,这些问题都是 NP 问题。
所以,按照定义,所有的 P 问题都是 NP 问题。
计算理论延伸出了图灵机理论,自动机=算法。
有两种自动机,一种是确定性自动机,机器从一个状态到另外一个状态的变化,只有一个分支可以走,而非确定性自动机,从一个状态到另外一个状态,有多个分支可以走。P 问题都可以用两种机器来解决,当非确定性自动机退化就变成了确定性自动机,而 NP 问题只能用非确定性自动机来解决。
自动机对 N 和 NP 问题的定义:
可以在确定性自动机以多项式时间解决的问题,称为 P 问题,可以在多项式时间验证答案的问题称为 NP 问题。而 NP 问题是可以在非确定型自动机以多项式时间解决的问题(NP 两字为 Non-deterministicPolynomial 的缩写,非确定多项式)。
数学,计算机科学,哲学,三个学科其实交融在一起,自动机是一台假想的机器,世界其实也可以认为是一个假想的机器,所以世界可以等于一台自动机吗,大家可以发挥想象力,在以后的日子里慢慢体会,建议购买书籍《计算理论》补习相关知识。
二、NPC 和 NP-hard 问题
存在这样一个 NP 问题,所有的 NP 问题都可以约化成它。换句话说,只要解决了这个问题,那么所有的 NP 问题都解决了。其定义要满足2个条件:
- 它得是一个
NP问题。 - 所有的
NP问题都可以约化到它。
这种问题称为 NP 完全问题(NPC)。按照这种定义,NP 问题要比 NPC 问题的范围广。
那什么是 NP-hard 问题,其定义要满足2个条件:
- 所有的
NP问题都可以约化到它。 - 它不是一个
NP问题。
也就是说,NP-hard 问题更难,你只要解决了 NP-hard 问题,那么所有的 NP 问题都可以解决。但是,这个问题本身不是一个 NP 问题,也就是解不能在多项式时间内被验证。
比如你有一个交际网,每个人是一个节点,认识的人之间相连。你要通过一个最快、最省钱、最能提升你个人形象、最没有威胁、最不影响你日常生活的方式认识一个萌妹,你怎么证明你认识这个萌妹是最省钱的呢?-来自知乎回答。
我们一旦发现一个问题是 NPC 问题,那么我们很难去准确求出其解,只能暴力枚举,靠猜。
三、总结
各类问题可以用这个图来表示:

“P=NP“ 问题的目标,就是想要知道 P 和 NP 这两个集合是否相等。为了证明两个集合( A 和 B)相等,一般都要证明两个方向:
-
A包含B。 -
B包含A。
我们已经说过 NP 包含了 P。因为任何一个非确定性机器,都能被当成一个确定性的机器来用。你只要不使用它的“超能力”,在每个分支点只探索一条路径就行。文章来源:https://www.toymoban.com/news/detail-438266.html
所以 “P=NP“ 就在于 P 是否也包含了 NP。也就是说,如果只使用确定性计算机,能否在多项式时间之内,解决所有非确定性计算机能在多项式时间内解决的问题。文章来源地址https://www.toymoban.com/news/detail-438266.html
到了这里,关于Go数据结构----你必须知道的一些的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!