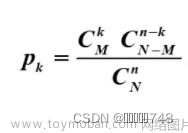随机游动的基本模型:
直线上的一个质点,每经过一个单位时间,分别以概率p,q向右或向左移动一格,若该点在时刻0从原点出发,而且每次移动是相互独立的。
用随机变量描述质点的运动 (无限制随机游动的结果)
设n时刻质点向右移动k次,则必然向左移动了n-k次,于是质点的位置即S=2k-n
故S的概率分布为
两端带有吸收壁的随机游动
假设在t=0的时刻,质点位于x=a,在x=0和x=a+b处各有一个吸收壁
记 为质点在n而最终在0被吸收的概率
为质点在n而最终在0被吸收的概率
显然可以看出的是
通过全概率公式可以得到 通过整理可以得到递推公式
通过整理可以得到递推公式  通过边界条件求解差分方程最终可以得到
通过边界条件求解差分方程最终可以得到
 而最终在a+b被吸收的概率为
而最终在a+b被吸收的概率为
其中当p=q=1/2时,该模型即为赌徒破产模型
其中质点位于a表示本金为a元,在a+b被吸收意味着再赢b元则停止赌博,p为赢的概率,在0处则代表破产,而此时破产的概率即为 这个结果直观的说明了在本金有限的情况下,贪心b越大,输光 的概率就越大,如果一直赌下去,必定全部输光。
这个结果直观的说明了在本金有限的情况下,贪心b越大,输光 的概率就越大,如果一直赌下去,必定全部输光。
进一步了解赌徒破产模型
假设有n个赌徒,每个人的赌资为 则全部赌徒的赌资为
则全部赌徒的赌资为 则第i个赌徒输光的概率为
则第i个赌徒输光的概率为 ,如果每个人的赌资有限,且人数足够多,则每个人破产的概率都接近于1。随着时间的推移,大部分人破产,赌资陆续向少数赌徒集中,这就是赌庄形成的过程。然后赌庄也会破产,继而形成新的赌庄。而非公平博弈则保证了赌庄的长盛不衰。
,如果每个人的赌资有限,且人数足够多,则每个人破产的概率都接近于1。随着时间的推移,大部分人破产,赌资陆续向少数赌徒集中,这就是赌庄形成的过程。然后赌庄也会破产,继而形成新的赌庄。而非公平博弈则保证了赌庄的长盛不衰。
游程(连续的成功和失败)
关于虚构数据的粗糙判断
游程数的概率分布
预备结论
 的非负整数解共有
的非负整数解共有 个
个
理解将m个不可区分的球放入r个可区分的盒子,可以模拟为某个向量包含r-1个1,和m个0,则该向量的维数为r+m-1,不同向量个数为
 的正整数解共有
的正整数解共有
理解将m-r个不可区分的球,放入r个盒子
独立重复投掷一枚(不必均匀)硬币n次时得到了m个反面,用1和0分别表示正面和反面,依次记录1,0构成的有限序列,用R表示其中0游程的个数,计算P(R=r)
总事件个数为

xj表示第j个0游程的长度,故
 的解个数即为可能情况数
的解个数即为可能情况数
对于每一组固定的x向量,讨论1游程的情况,和0游程区别于两端的情况,通过加1做等价替换,最终为满足方差
 的正整数解
的正整数解
由古典概型可知

n=100,m=47时得到的数据结果
r |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
|
0.064 |
0.102 |
0.137 |
0.157 |
0.154 |
0.129 |
0.092 |
0.056 |
譬如游程数大于35或小于16都是概率极小10^(-4)级数的概率,故譬如大牌的时候,必然有许多次好牌连续出现,或许多次臭牌连续出现
应用运动员的情绪问题
情景:在保龄球比赛中,一次击倒10个为全中,用X表示,第二次击倒为补中,用L表示,若第二次仍不中则为失误。可以通过L的游程数判断运动员的发挥是否正常,即心理素质。
假设心理素质很好,击出补中概率不变,则若补中次数为4,在12次击球中位置是任意排列的,则有r个游程的概率为 可以计算得到
可以计算得到
r |
1 |
2 |
3 |
4 |
|
0.0182 |
0.2182 |
0.5091 |
0.2545 |
所以若心态良好,至少出现两个游程
游程长度的概率分布
第一个游程长度的概率分布(几何分布)

n第独立重复实验,游程的最大长度推导可得
 文章来源:https://www.toymoban.com/news/detail-439192.html
文章来源:https://www.toymoban.com/news/detail-439192.html
结论连投100次,游程长度大于等于4的概率与等于0.9727;连续投50次很可能出现不少于5次的连续正面文章来源地址https://www.toymoban.com/news/detail-439192.html
到了这里,关于概率论专题-随机游动(复习笔记自用)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!