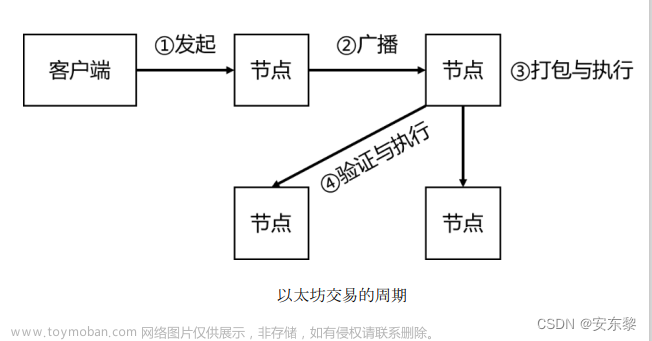
目录
阻抗圆图
归一化阻抗:
电长度:
Smith Chart的基本构成:
Smith Chart特点:
由阻抗求导纳:
导纳圆图
阻抗圆图
归一化阻抗:
圆图上均采用归一化阻抗




其中:

将反射系数进行虚实分解

电长度:
传输线长度除以工作波长𝑙/𝜆,圆图上通常标注电长度,而不是角度
Smith Chart的基本构成:
1)等反射系数圆

可见,反射系数在复平面上表示一个半径为|𝛤|的圆
对于均匀无耗传输线,负载确定后,反射系数的模值就确定了

由𝜑=𝜑𝐿−2𝛽𝑧可知:
向波源方向,z增大,𝜑减小,顺时针旋转
向负载方向,z减小,𝜑增大,逆时针旋转
线上移动𝜆/2长度,沿反射系数圆旋转一周
2)等电阻圆



所有圆相切于(1,0)点
3)等电抗圆



所有圆相切于(1,0)点
Smith Chart特点:
1)三个特殊点

开路点D(1,0):

短路点C(-1,0):

匹配点O(0,0):

2)三条特殊线
正实轴:电压波腹点轨迹,𝑋=0,𝑅的读数即为驻波比𝜌的读数
负实轴:电压波节点轨迹,𝑋=0,𝑅的读数即为行波系数𝑘的读数
单位圆:𝑅=0的轨迹,即全反射系数圆的轨迹
3)两个特殊面
上半平面:感性阻抗𝑋>0轨迹
下半平面:容性阻抗𝑋<0轨迹
4)两个旋转方向
顺时针:向波源
逆时针:向负载
5)圆图上任一点
必然是一个等电阻圆和等电抗圆的交点
同时也对应一个等反射系数圆,可以通过读驻波比来推出反射系数模值
对应着四个参量:

由阻抗求导纳:
归一化阻抗点A关于原点o的对称点A'即为归一化导纳点

导纳圆图
1)阻抗圆图不旋转,圆图可以表示电流反射系数、归一化电纳、归一化电导之间的关系文章来源:https://www.toymoban.com/news/detail-439278.html
2)阻抗圆图旋转180°,圆图可以表示电压反射系数、归一化电纳、归一化电导之间的关系。此时(1,0)点为短路点,(-1,0)点为开路点,正实轴为波节点轨迹,负实轴为波腹点轨迹文章来源地址https://www.toymoban.com/news/detail-439278.html
到了这里,关于《微波原理与技术》学习笔记3传输线理论-史密斯圆图(Smith Chart)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!