1. 傅里叶变换理论层面理解
数学意义:傅里叶变换将一个任意的周期函数分解成为无穷个正弦函数的和的形式物理效果:傅里叶变换实现了将信号从空间域到频率域的转换信号分析: 一维傅里叶变换(将杂乱的信号由时域转化到频域中)一维傅里叶变化是将信号分解为正弦波的和的形式
时域横轴是时间,纵轴是振幅
频域横轴是频率,纵轴是振幅
对一个信号做时域到频域的变换,能够清除看到该信号主要由两个正弦波以及一些噪声混合,如下图所示:

将有效的信号频率提取并分离拟合出信号信息,然后将噪声过滤掉,得到滤波结果
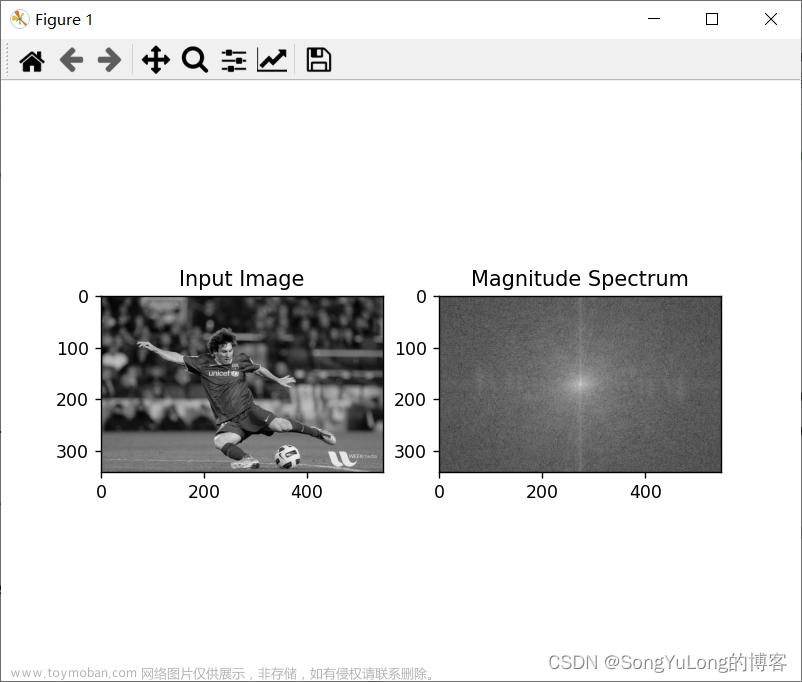
频谱图: 二维傅里叶变换 (原图中的像素值是x,y坐标轴下的(即空间域),而傅立叶变换后的像素值是u,v坐标轴下的(即频域)),二维傅里叶变换可以将一个二维信号(图像)分解为三角平面波之和的形式
二维信号的离散傅里叶变换所得到的结果的频率成分的分布如下所示:
在经过频谱居中后的频谱中,中间最亮的点是最低频率,属于直流分量(DC分量)。越往边外走,频率越高。所以,频谱图中的四个角和X,Y轴的尽头都是高频(未经过频谱居中的相反)
二维离散傅里叶变换的作用:可以将空间域(二维灰度数表)的图像转换到频域(频率数表),使得更直观地观察和处理图像,也更有利于进行频域滤波等操作。
一副图像(不论是灰度的图像还是彩色图像)所提供的信息都是显而易见的(排除一些本身就很抽象的图片,不搞艺术哈哈哈)。然而,一副图像的傅里叶频谱图,却常常让人难以理解,满脸问号,一脸蒙B。
2. 常见频谱图
单色图
只有一种颜色
正弦波
分析:频率越低对称的频点越靠近频谱中心,随着频率增加远离中心(因为中心是低频,两端为高频)
灰度变化
分析:图像灰度变化方向体现在频谱图的方向中
根据上面两个信息可以得到下面结果:
常见几何形状
分析:还是和上面讲解的一样,频谱图的绘制规律是朝着梯度变化的方向改变的
这边可以这样理解傅里叶变换:第一种理解: 二维图像进行傅里叶变化得到的频谱图(图像梯度的分布图),当然频谱图上的各点与原图像各点并不存在一一对应关系,即使在不移频的情况下也不对应。傅里叶频谱图上看到的明亮不一的亮点,实际上图像上某一点的像素灰度值与它的邻域点差异的强弱,即梯度的大小,也即该点的频率的大小(也可以这么理解,低频部分指低梯度的点,高频部分指高梯度的点)。另一种理解:图像二维频谱图通过对输入图像进行水平和竖直两个方向的所有扫描线的一维傅立叶变换进行叠加得到,用来表示输入图像的频率分布。
频谱图以图像的中心为圆心,圆的相位对应原图中频率分量的相位,半径对应频率高低。低频部分半径小,高频对应的半径较大,中心为直流分量(图像灰度的平均值),某点的灰度值对应该频率的能量高低。
3. 傅里叶变换在图像中的应用
Opencv中的傅里叶变换实现
实现步骤:文章来源:https://www.toymoban.com/news/detail-439318.html
- getOptimalDFTSize()函数得到DFT变换后结果的最优尺寸大小
- 根据得到的尺寸大小,使用copyMakeBorder()函数填充图像,得到填充后的Mat
- 根据新生成的Mat,使用merge()函数得到一个双通道的Mat,命名为planes
- 使用dft()函数进行傅里叶变换,得到通道1为实部,通道2为虚部
实现代码如下所示:文章来源地址https://www.toymoban.com/news/detail-439318.html
image.convertTo(image, CV_32F);
vector<Mat> channels;
split(image, channels); //分离RGB通道
Mat image_B = channels[0]到了这里,关于最详细的图像傅里叶变换的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!