排序篇：归并排序的递归，非递归以及计数排序的实现(C语言)-Toy模板网

这篇具有很好参考价值的文章主要介绍了排序篇：归并排序的递归，非递归以及计数排序的实现(C语言)。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一：归并排序

(1)归并排序的基本思想

(2)递归版本

①实现思路

②合并

③递归实现有序

④最终代码

(3)非递归版本

①实现思路

②控制分组

③最终代码

(4)时间，空间复杂度分析

(5)小结

二：计数排序

(1)计数排序的基本思想

(2)实现思路

(3)图解加最终代码

(4)时间，空间复杂度分析

(5)小结

一：归并排序

(1)归并排序的基本思想

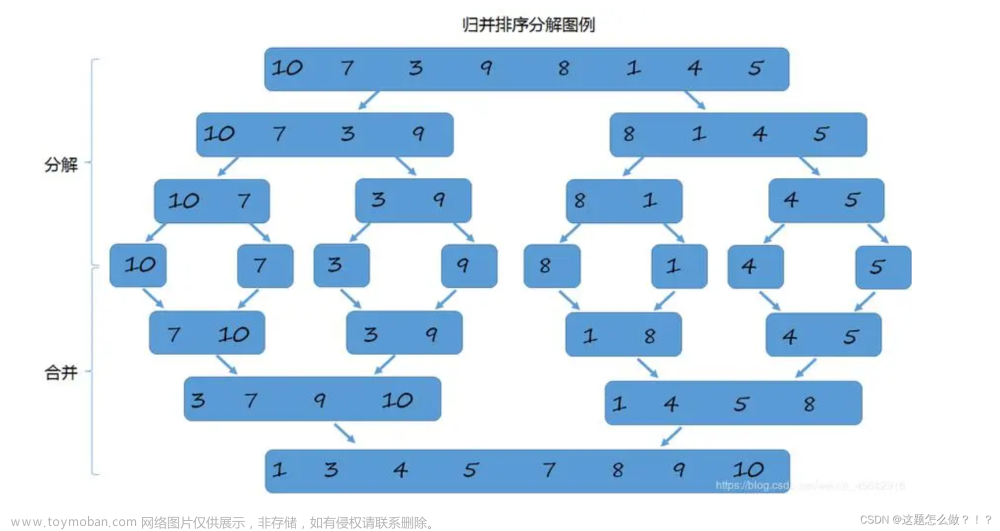
归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。
将已有序的子序列合并，得到完全有序的序列；
即先使每个子序列有序，再使子序列段间有序。若将两个有序数组合并成一个有序数组，称为二路归并。

图解：

(2)递归版本

①实现思路

【1】把待排序数组从中间分成两个子数组，直到无法分割（即每个子数组只有一个元素)。

【2】对每个子数组进行归并排序，即递归调用归并排序函数。

【3】合并两个有序子数组，得到一个有序的数组(这里需要辅助数组来实现)，然后把这个有序数组拷贝到原数组中。

【4】重复步骤3，直到所有的子数组合并成一个有序的数组，排序完成。

②合并

合并两个有序数组需要辅助数组tmp，大致思路就是遍历两个区间，拿出两个数组中较小值放在tmp中，合并成有序后再拷贝回原数组。

图解：

排序篇：归并排序的递归，非递归以及计数排序的实现(C语言)

这里循环已经结束但我们需要把没结束的一方拷贝到tmp中

    //把没结束的一方拷贝到tmp中
	while (begin1 <= end1)
	{
		tmp[i++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[i++] = a[begin2++];
	}

合并的代码：

//这个时候左右已经有序，合并
	int begin1 = left;
	int end1 = mid;
	int begin2 = mid + 1;
	int end2 = right;
	int i = left;

	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin2] < a[begin1])
		{
			tmp[i++] = a[begin2++];
		}
		else
		{
			tmp[i++] = a[begin1++];
		}
	}

	//把没结束的一方拷贝到tmp中
	while (begin1 <= end1)
	{
		tmp[i++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[i++] = a[begin2++];
	}

	//拷贝回去
	//注意这里合并了的有序区间为[left,right]
	//别的区间不一定有序，拷贝时要注意
	for (int j = left; j <= right; j++)
	{
		a[j] = tmp[j];
	}

③递归实现有序

图解(以左区间为例)：

④最终代码

void _MergeSort(int* a, int left,int right,int* tmp)
{
	//只有一个元素(可看成有序)或者区域不存在，返回
	if (left >= right)
	{
		return;
	}
	int mid = left + (right - left) / 2;
	//先递归排序左区间，后递归排序右区间
	_MergeSort(a, left, mid, tmp);
	_MergeSort(a, mid + 1, right, tmp);

	//这个时候左右已经有序，合并
	int begin1 = left;
	int end1 = mid;
	int begin2 = mid + 1;
	int end2 = right;
	int i = left;

	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin2] < a[begin1])
		{
			tmp[i++] = a[begin2++];
		}
		else
		{
			tmp[i++] = a[begin1++];
		}
	}

	//把没结束的一方拷贝到tmp中
	while (begin1 <= end1)
	{
		tmp[i++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[i++] = a[begin2++];
	}

	//拷贝回去
	//注意这里合并了的有序区间为[left,right]
	//别的区间不一定有序，拷贝时要注意
	for (int j = left; j <= right; j++)
	{
		a[j] = tmp[j];
	}
}
//归并排序
void MergeSort(int* a, int n)
{
	//临时数组
	int* tmp = (int*)malloc(sizeof(int) * n);
	
	//调用子函数进行排序
	_MergeSort(a, 0,n-1,tmp);

	//销毁
	free(tmp);
	//这里置不置空没影响
	tmp = NULL;
}

(3)非递归版本

①实现思路

【1】首先将待排序数组中的每一个元素看成是一个大小为1的有序区间。

【2】然后将相邻的两个区间(保证每次合成的都是相邻区间，依靠间距gap来控制)合并成一个更大的有序区间，这可以通过归并排序中的合并操作来实现。

【3】重复步骤2，每次将相邻的两个有序子数组合并成更大的有序子数组，直到得到一个完整的有序数组。

【4】最终得到的有序数组就是排序结果。

②控制分组

关于间距gap对循环的控制：

gap=1，范围为1(gap)的区间是有序的，合并相邻两个区间，拷贝。

gap=gap*2=2，范围为2(gap)的区间是有序的，合并相邻两个区间，拷贝。

gap=gap*2=4，范围为4(gap)的区间是有序的，合并相邻两个区间，拷贝。

………………

一直到gap>=n(这个时候数组前n个数一定有序，n是数组元素个数，结束循环)

代码：
    int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i;
			int end1 = i + gap - 1;
			int begin2 = i + gap;
			int end2 = i + gap * 2 - 1;
			int index = i;

			while (begin1 <= end1 && begin2 <= end2)
			{
				//begin1小，放a[begin1]
				if (a[begin1] < a[begin2])
				{
					tmp[index++] = a[begin1++];
				}
				else
				{
					tmp[index++] = a[begin2++];
				}
			}

			while (begin1 <= end1)
			{
				tmp[index++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[index++] = a[begin2++];
			}
			//排序一组拷贝一组
			for (int j = i; j <= end2; j++)
			{
				a[j] = tmp[j];
			}
		}
		gap *= 2;
	}
图解：

我们可以看到像前面那样进行分组是有很大可能越界的，那我们应该怎么做呢？

在合并拷贝前加上区间判断和修正后，排序不会越界了

③最终代码

//归并非递归
void MergeSortNonR(int* a, int n)
{
	//临时数组
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		printf("malloc error\n");
		exit(-1);
	}

	int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i;
			int end1 = i + gap - 1;
			int begin2 = i + gap;
			int end2 = i + gap * 2 - 1;
			int index = i;

			//end1,begin2,end2都有可能越界
			if (end1 >= n || begin2 >= n)
			{
				break;
			}
			if (end2 >= n)
			{
				end2 = n - 1;
			}

			while (begin1 <= end1 && begin2 <= end2)
			{
				//begin1小，放a[begin1]
				if (a[begin1] < a[begin2])
				{
					tmp[index++] = a[begin1++];
				}
				else
				{
					tmp[index++] = a[begin2++];
				}
			}

			while (begin1 <= end1)
			{
				tmp[index++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[index++] = a[begin2++];
			}
			//排序一组拷贝一组
			for (int j = i; j <= end2; j++)
			{
				a[j] = tmp[j];
			}
		}
		gap *= 2;
	}

	//释放
	free(tmp);
	tmp = NULL;
}

(4)时间，空间复杂度分析

空间复杂度：

开辟了空间大小和原数组相同的辅助数组，故空间复杂度为O(N)

时间复杂度：

【1】在归并排序的每一次合并操作中，需要将两个有序数组合并成一个有序数组，这个过程需要比较两个有序数组中所有元素，因此时间复杂度为O(N)。

【2】在归并排序中，每次将数组划分成两个长度大致相等的子数组，因此可以得到一个完全二叉树，其深度大约为logN。每层的合并操作的时间复杂度为O(N)，因此整个算法的时间复杂度为O(N*logN)。

(5)小结

归并排序的效率还不错，但是有O(N)的空间复杂度，更多是应用在解决磁盘中的外排序问题。

另外控制边界的方法并不止上面一种

除了右区间不在数组中(左右都越界)直接跳出(这个时候没有对tmp进行操作，对应位置为随机值)

我们也可以把右区间人为修改为不存在(begin>end)，这种情况下即使不需要合并也会拷贝到tmp中，我们就可以一次大循环结束再进行拷贝(拷贝一层)，但是这样不是很好理解

代码：
//归并非递归
void MergeSortNonR1(int* a, int n)
{
	//临时数组
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		printf("malloc error\n");
		exit(-1);
	}

	int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i += 2*gap)
		{
			int begin1 = i;
			int end1 = i + gap - 1;
			int begin2 = i + gap;
			int end2 = i + gap * 2 - 1;
			int index = i;

			//修正，让左区间不越界
			if (end1 >= n)
			{
				end1 = n - 1;
			}
			//修正，让右区间不存在
			if (begin2 >= n)
			{
				//begin2 > end2，区间不存在
				begin2 = n ;
				end2 = n - 1;
			}
			//修正，让右区间不越界
			if (end2 >= n)
			{
				end2 = n - 1;
			}

			while (begin1 <= end1 && begin2 <= end2)
			{
				//begin1小，放a[begin1]
				if (a[begin1] < a[begin2])
				{
					tmp[index++] = a[begin1++];
				}
				else
				{
					tmp[index++] = a[begin2++];
				}
			}

			while (begin1 <= end1)
			{
				tmp[index++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[index++] = a[begin2++];
			}

		}
		//一层按组排序完，拷贝
		for (int j = 0; j < n; j++)
		{
			a[j] = tmp[j];
		}
		gap *= 2;
	}
	
	//释放
	free(tmp);
	tmp = NULL;
}

二：计数排序

(1)计数排序的基本思想

对于给定的输入序列中的每一个元素x，确定出小于x的元素个数

这样就可以直接把x放到以小于x的元素个数为下标的输出序列的对应位置上。

(这里其实是相对位置的概念，比如数组中最小值为0，它对应下标0位置，最小值为1000，也是对应下标0位置)

(2)实现思路

【1】遍历一遍，找出最大值和最小值

【2】依据最大值和最小值的差值来开辟辅助数组tmp

【3】计数，记录数组元素出现次数

【4】遍历tmp数组，进行拷贝

(3)图解加最终代码

图解：

排序篇：归并排序的递归，非递归以及计数排序的实现(C语言)

最终代码：

//计数排序
void CountSort(int* a, int n)
{
	//找出最大和最小
	int max = a[0];
	int min = a[0];
	int i = 0;
	for (int i = 1; i < n; i++)
	{
		if (a[i] > max)
		{
			max = a[i];
		}
		if (a[i] < min)
		{
			min = a[i];
		}
	}

	//开空间加初始化
	int* tmp = (int*)malloc(sizeof(int) * (max - min + 1));
	if (tmp == NULL)
	{
		printf("malloc error\n");
		exit(-1);
	}
	//必须初始化为0
	memset(tmp, 0, sizeof(int) * (max - min + 1));

	//计数
	for (i = 0; i < n; i++)
	{
		tmp[a[i]-min]++;
	}

	//拷贝
	int j = 0;
	for (i = 0; i < max - min + 1; i++)
	{
		while (tmp[i]--)
		{
			a[j++] = i + min;
		}
	}
}

(4)时间，空间复杂度分析

空间复杂度：

开辟了空间大小为range(max-min+1)的辅助数组，故空间复杂度为O(range)

空间复杂度：

遍历a找最大和最小为O(N)

遍历a计数为O(N)

遍历range为O(range)

故时间复杂度为O(max(N,range))

(5)小结

计数排序是一种非比较的排序，它不需要进行数据间的比较。

算法设计上非常巧妙，时间复杂度最快可以达到O(N)，但是有一定的局限性

比如正负数同时存在或者数据大小浮动很大(1,2,3,1000000)的情况，可能导致空间的大量浪费，效率也会有所下降。文章来源地址https://www.toymoban.com/news/detail-439704.html

到了这里，关于排序篇：归并排序的递归，非递归以及计数排序的实现(C语言)的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！