数学建模之秩和比综合评价方法（RSR）-Toy模板网

这篇具有很好参考价值的文章主要介绍了数学建模之秩和比综合评价方法（RSR）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

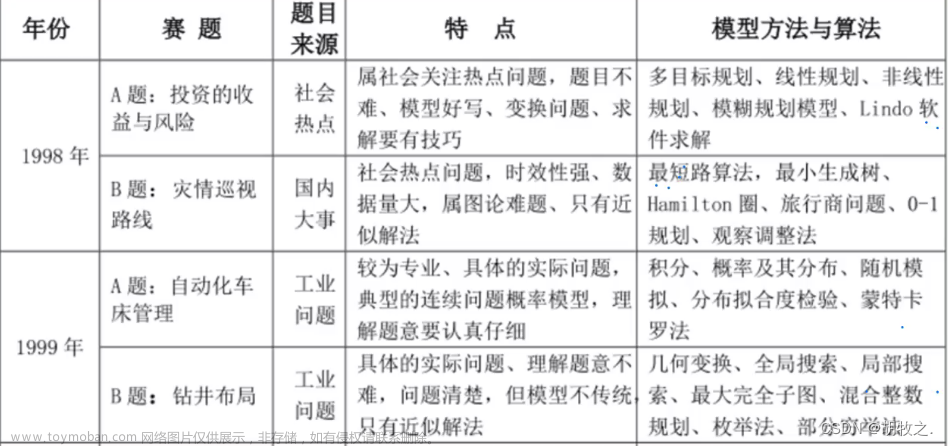
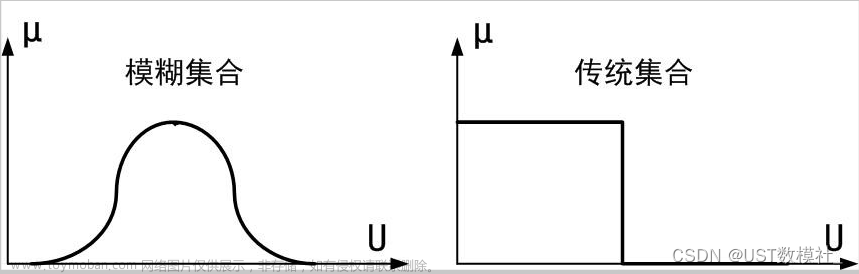
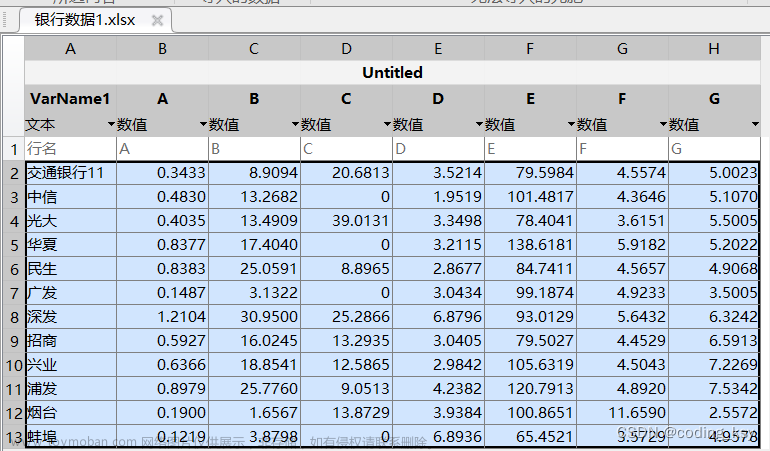
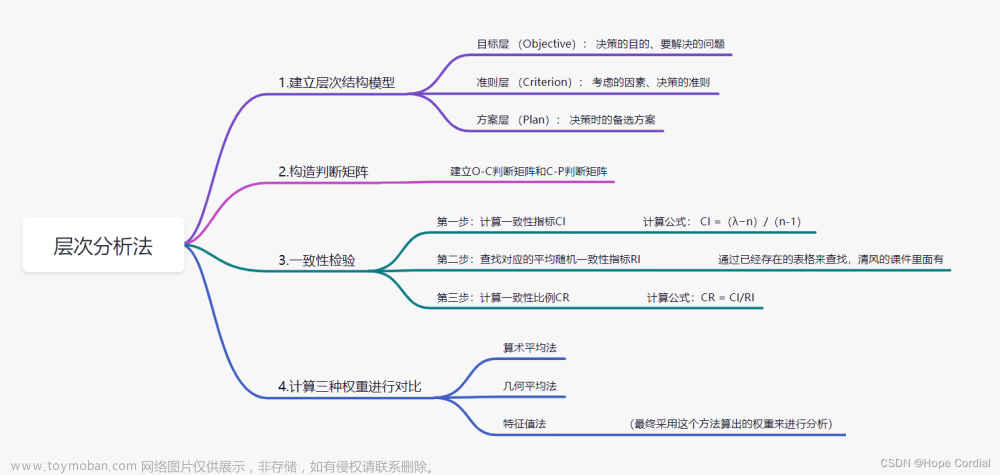
本文参考的是司守奎，孙兆亮主编的数学建模算法与应用（第二版）

秩和比综合评价方法（RSR）在医疗卫生领域的多指标综合评价、统计预测预报、统计质量控制等方面已经得到了广泛应用。

其中秩序和比是行或者列秩次的平均值，是一个非参数的统计量，具有0-1连续变量的特征。

下面介绍秩和比综合评价方法的一般步骤：

第一步，数据预处理。凡是评价方法中，都需要面对效益型、区间型、成本型等指标。一般的情况都是将非效益型指标转换为效益型指标，因为这样能够直接通过数值大小进行指标优劣的评判，方便后续工作的展开。

第二步，编秩。由于已经数据预处理过，那么编秩，按照数值从小到大编即可，也就是给给数值一个正整数序号，序号根据数值从小到大也从小到大给，数值相同则给同样的序号。
数学建模之秩和比综合评价方法（RSR）

第三步，确定权重，计算秩和比。权重的确立可以通过熵权法或者层次分析法等获得。

数学建模之秩和比综合评价方法（RSR）
第四步，计算概率单位。

数学建模之秩和比综合评价方法（RSR）
第五步，计算直线回归方程。

第六步，分档排序，得出评价。

数学建模之秩和比综合评价方法（RSR）
下面展示一道例题：

第一步，数据预处理。

data = [75.2 3.5 38.2 370.1 101.5 10.0
    76.1 3.3 36.7 369.6 101.0 10.3
    80.4 2.7 30.5 309.7 84.8 10.0
    77.8 2.7 36.3 370.1 101.4 10.2
    75.9 2.3 38.9 369.4 101.2 9.61
    74.3 2.4 36.7 335.3 91.9 9.2
    74.6 2.2 37.5 356.2 97.6 9.3
    72.1 1.8 40.3 401.7 101.1 10.0
    72.8 1.9 37.1 372.8 102.1 10.0
    72.1 1.5 33.2 358.1 97.8 10.4
    ];%待评价指标

data(:,[2,6]) = -data(:,[2,6]);%数据预处理，将成本型指标转换为效益性

第二步，编秩。

ra = tiedrank(data)%编秩，即对每个指标各自进行排序

第三步，确定权重，计算加权秩和比。

数学建模之秩和比综合评价方法（RSR）

weight = [0.093 0.418 0.132 0.100 0.098 0.159];%各指标的权重
[row,col] = size(data);% 获取数据的维度信息
RSR = mean(ra, 2)/row;% 计算秩和比
W = repmat(weight, [row,1]);
WRSR = sum(ra.*W, 2)/row;%计算加权秩和比
[sWRSR, ind] = sort(WRSR)%对加权秩合比排序

第四步，计算概率单位。

p = [1:row] / row; %计算累计频率
p(end) = 1 - 1 / (4 * row) %修正最后一个累计频率，最后一个累计频率按1-1/（4n）估计
probit = norminv(p,0,1) + 5 % 计算标准正太分布的p分位数+5

第五步，计算直线回归方程。

x = [ones(row,1),probit'];% 构造一元线性回归分析的数据矩阵
[ab, abint, r, rint, stats] = regress(sWRSR,x)

第六步，分档排序，得出评价。
数学建模之秩和比综合评价方法（RSR）

WRSRfit = ab(1) + ab(2) * probit; % 计算WRSR的估计值
WRSRfit'
y = [1983:1992];
y(ind)'

matlab完整代码如下：文章来源地址https://www.toymoban.com/news/detail-439915.html

clc,clear
data = [75.2 3.5 38.2 370.1 101.5 10.0
    76.1 3.3 36.7 369.6 101.0 10.3
    80.4 2.7 30.5 309.7 84.8 10.0
    77.8 2.7 36.3 370.1 101.4 10.2
    75.9 2.3 38.9 369.4 101.2 9.61
    74.3 2.4 36.7 335.3 91.9 9.2
    74.6 2.2 37.5 356.2 97.6 9.3
    72.1 1.8 40.3 401.7 101.1 10.0
    72.8 1.9 37.1 372.8 102.1 10.0
    72.1 1.5 33.2 358.1 97.8 10.4
    ];%待评价指标
weight = [0.093 0.418 0.132 0.100 0.098 0.159];%各指标的权重
data(:,[2,6]) = -data(:,[2,6]);%数据预处理，将成本型指标转换为效益性

ra = tiedrank(data)%编秩，即对每个指标各自进行排序
[row,col] = size(data);% 获取数据的维度信息
RSR = mean(ra, 2)/row;% 计算秩合比
W = repmat(weight, [row,1]);
WRSR = sum(ra.*W, 2)/row;%计算加权秩和比
[sWRSR, ind] = sort(WRSR);%对加权秩合比排序

p = [1:row] / row; %计算累计频率
p(end) = 1 - 1 / (4 * row) %修正最后一个累计频率，最后一个累计频率按1-1/（4n）估计
probit = norminv(p,0,1) + 5 % 计算标准正太分布的p分位数+5


x = [ones(row,1),probit'];% 构造一元线性回归分析的数据矩阵
[ab, abint, r, rint, stats] = regress(sWRSR,x)
WRSRfit = ab(1) + ab(2) * probit; % 计算WRSR的估计值
WRSRfit'
y = [1983:1992];
y(ind)'