奇异值分解(singular value decomposition,SVD),已经成为矩阵计算中最有用和最有效的工具之一,并且在最小二乘问题、最优化、统计分析、信号与图像处理、系统理论与控制等领域得到广泛应用。
首先我们都知道方阵是可以特征值分解的,那么问题来了,如果矩阵不是一个方阵那么它还可以分解吗?是可以的,就是我们正在介绍的奇异值分解。
那么,开冲!

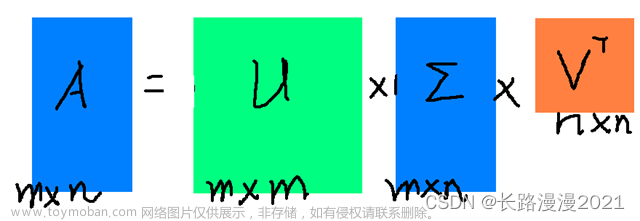
下面介绍方法,记住任何一个矩阵A都可以分解成以下形式(别问为什么,我看了证明的,头大,太难了)

注:U和V都是酉矩阵,即满足
求法如下
U是 的特征向量张成的一个矩阵
的特征向量张成的一个矩阵
V是 的特征向量张成的一个矩阵
的特征向量张成的一个矩阵
 是
是 或者
或者 的特征值的平方根
的特征值的平方根
下面进行一个证明

注: 和
和 的特征值是一样的
的特征值是一样的
好了,SVD分解就是这么简单,一般就两步
第一步:求 的特征向量(构成的矩阵就是V)和特征值(默认由大到小排列,然后要求根号)
的特征向量(构成的矩阵就是V)和特征值(默认由大到小排列,然后要求根号)
第二步:求 的特征向量(构成的矩阵就是U)
的特征向量(构成的矩阵就是U)
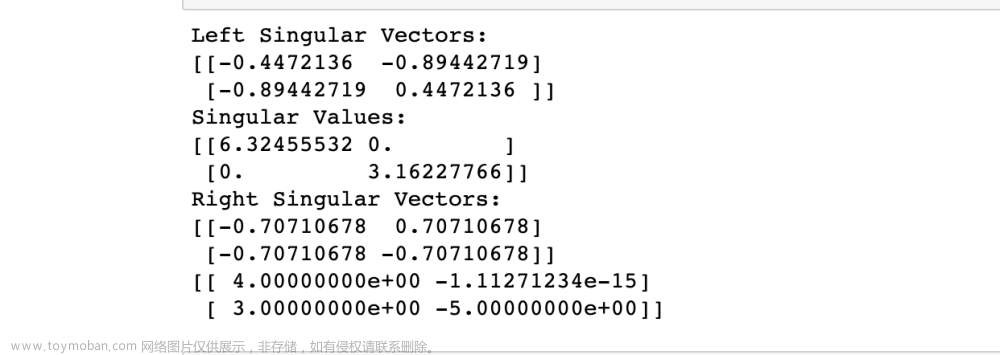
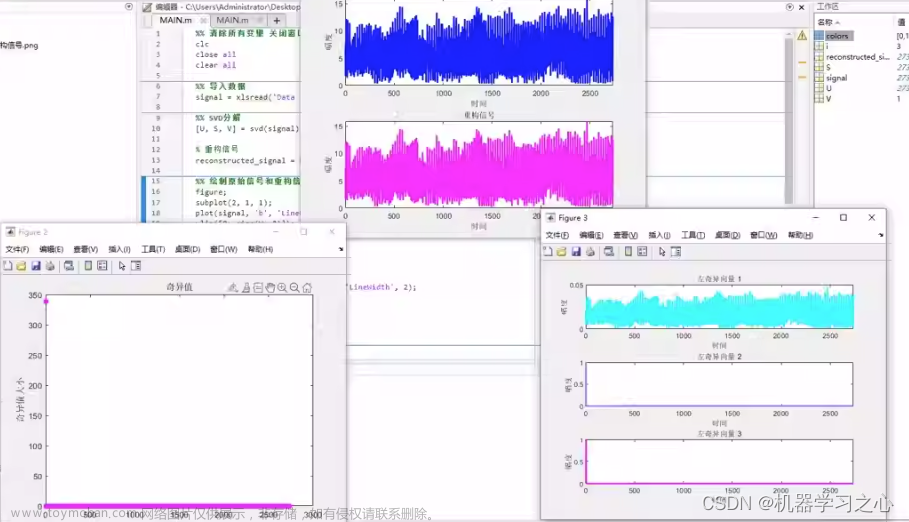
下面进行一个实例讲解:

 文章来源:https://www.toymoban.com/news/detail-440458.html
文章来源:https://www.toymoban.com/news/detail-440458.html
 文章来源地址https://www.toymoban.com/news/detail-440458.html
文章来源地址https://www.toymoban.com/news/detail-440458.html
到了这里,关于SVD,奇异值分解的计算步骤以及实例讲解的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!