1. Toy模板网首页
  2. > Toy博客

二叉树的实现（C语言数据结构）

10月前 作者：桜キャンドル淵 分类：Toy博客 阅读(38) 违法举报

这篇具有很好参考价值的文章主要介绍了二叉树的实现（C语言数据结构）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

目录

一、以下是我们需要实现的功能

二、以下是我们具体功能的实现

1.创建新的结点

2.通过数组生成二叉树

 3.先序遍历

4.中序遍历

5.后序遍历 

 6.层序遍历

7.计算二叉树的结点个数

8.查找指定值为x的结点

9.查找第K层的结点个数

10.统计二叉树叶子结点的个数

11.判断是否为完全二叉树

12.二叉树的销毁

13.求二叉树的高度

14.汇总

三、测试代码

一、以下是我们需要实现的功能

#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>
typedef char BTDataType;

typedef struct BinaryTreeNode
{
    BTDataType _data;
    struct BinaryTreeNode* _left;
    struct BinaryTreeNode* _right;
}BTNode;

BTNode* BuyNode(BTDataType x);

// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);
// 二叉树销毁
void BinaryTreeDestroy(BTNode** root);
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root);
// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root);

二、以下是我们具体功能的实现

1.创建新的结点

在下面的代码中，我们将调用我们的创建新的结点来快速创建结点。

TNode* BuyNode(BTDataType x)
{
    BTNode* node = (BTNode*)malloc(sizeof(BTNode));
    assert(node);

    node->_data = x;
    node->_left = NULL;
    node->_right = NULL;

    return node;
}

2.通过数组生成二叉树

BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{
//这里我们的a为我们的数组
//n为我们数组的最大长度
//pi为我们遍历数组的指针。
//这里我们使用'#'来表示NULL
//当我们所指向的位置的元素为#或者我们的指针已经超出了数组的范围的时候，我们就需要返回NULL
//并且将我们的指针后移。
    if(a[*pi] == '#' || *pi >= n)
    {
        printf("NULL ");
        (*pi)++;
        return NULL;
    }
//创建一个新的二叉树的结点
    BTNode *dst= BuyNode(a[*pi]);
    printf("%c ",dst->_data);
    (*pi)++;
//将我们之前开创的结点的左右指针指向数组中所对应的结点
//如果我们的对应数组中的数据不为空的话，我们的左右指针都会指向新的对应的结点
//如果我们的结点为空的话，我们会得到的返回值为NULL，
    dst->_left = BinaryTreeCreate(a,n,pi);
    dst->_right = BinaryTreeCreate(a,n,pi);

    return dst;
}

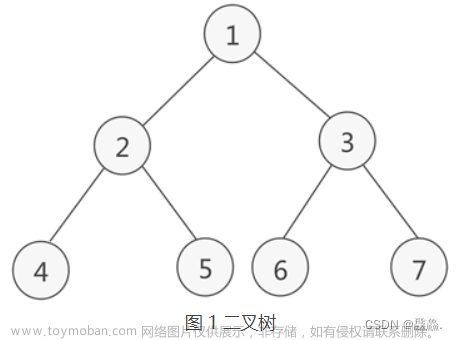
 就如我们在下面的代码中的数组，我们按照上面先序遍历的代码的描述，我们所创建出来的就是这样一棵二叉树二叉树的实现（C语言数据结构）

二叉树的实现（C语言数据结构）

 3.先序遍历

先序遍历就是先遍历我们的根节点，然后遍历我们左子树，然后遍历我们的右子树。

//先序遍历
void BinaryTreePrevOrder(BTNode* root)
{
//如果我们根节点的等于NULL，我们就直接返回上一层递归
    if(root == NULL)
    {
        return;
    }
//将我们当前结点中的数据打印出来
    printf("%c ",root->_data);
//遍历我们的左树
    BinaryTreePrevOrder(root->_left);
//遍历我们的右树
    BinaryTreePrevOrder(root->_right);
}

我们上面代码进行先序遍历所生成的序列是这样的

二叉树的实现（C语言数据结构）

 二叉树的实现（C语言数据结构）

4.中序遍历

中序遍历就是先读取我们左子树中的元素，再读取我们根节点的元素，最后再读取右子树中的元素。

// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{
    if(root == NULL)
    {
        return;
    }
    BinaryTreeInOrder(root->_left);
    printf("%c ",root->_data);
    BinaryTreeInOrder(root->_right);
}

二叉树的实现（C语言数据结构）

 二叉树的实现（C语言数据结构）

5.后序遍历 

后序遍历就是先遍历我们的左子树，再遍历我们右子树，最后遍历我们的根节点

void BinaryTreePostOrder(BTNode* root)
{
    if(root == NULL)
    {
        return;
    }
    BinaryTreePostOrder(root->_left);
    BinaryTreePostOrder(root->_right);
    printf("%c ",root->_data);
}

从下面的顺序中，我们发现我们最后才遍历了根节点 

二叉树的实现（C语言数据结构）

 二叉树的实现（C语言数据结构）

 6.层序遍历

层序遍历就是先将我们二叉树的根节点入队，然后再将我们根节点的左右指针所指向的结点入队，然后将我们队首的元素出队。

这里我们需要用到一个队列，具体的队列的代码我们在下面的汇总代码中将会给出。

// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
//创建我们的队列
    Queue q;
//初始化队列
    QueueInit(&q);
    assert(root);
//将我们的根节点入队列
    QueuePush(&q, root);
//如果我们的栈空间不为空的话就继续我们的循环
    while(!QueueEmpty(&q))
    {
//创建一个临时变量结点获得我们队列头的结点
        BTNode *temp= QueueFront(&q);
//将我们队列头的数据打印
        printf("%c ",temp->_data);
//将我们队列头的左右指针所对应的结点入队列
        if(temp->_left)
        {
            QueuePush(&q,temp->_left);
        }
        if(temp->_right)
        {
            QueuePush(&q,temp->_right);
        }
//将我们队头的结点出队
        QueuePop(&q);
    }
//销毁我们的队伍
    QueueDestory(&q);
}

7.计算二叉树的结点个数

// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
//如果我们当前的结点为空，也就是说我们已经到了叶子结点的左右结点，也就是没有结点
//所以我们需要返回0
    if(root==NULL)
    {
        return 0;
    }
//如果我们当前的结点的左指针和右指针都是空的话，也就是说这是我们的叶子结点
//就返回1，也就是只有一个结点。
    if(root->_left==NULL&&root->_right==NULL)
    {
        return 1;
    }
//使用递归遍历我们的二叉树，即分别统计我们左子树中的结点个数再加上右子树中的结点个数再加上1
//因为我们需要将我们当前所指的结点算上。
    return BinaryTreeSize(root->_left)+BinaryTreeSize(root->_right)+1;
}

8.查找指定值为x的结点

这里我们的目的是找到第一个指定值为x的结点，也就是说采用先序遍历是最佳的方法。因为先序遍历会首先找到所对应的结点然后将其返回，但是我们如果采用其他的遍历方式，由于先找到的不是根节点的元素，而是分别以左中右，和左右中的顺序来遍历，就会当根结点为我们的1目标结点时错过我们的根节点。

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
    if(root==NULL)
    {
        return NULL;
    }
    if(root->_data==x)
    {
        return root;
    }
    BinaryTreeFind(root->_left, x);
    BinaryTreeFind(root->_right,x);
}

9.查找第K层的结点个数

查找第k层，我们将我们的问题化为小问题，也就是我们第一层的结点需要往下找k-1层，第二层的结点需要往下找k-2层，以此类推，只有当我们的k为1的时候返回的就是我们需要找的k层的结点的个数的总和。

// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
    if(root==NULL)
    {
        return 0;
    }
    if(k==1)
    {
        return 1;
    }
//分别遍历我们的左右子树，并且将我们的k的参数--,当我们的k为1时，就到达了我们所想要查找对应的层。
    return BinaryTreeLevelKSize(root->_left, k-1)+BinaryTreeLevelKSize(root->_right, k-1);
}

10.统计二叉树叶子结点的个数

// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
    if(root==NULL)
    {
        return 0;
    }
//如果我们的结点的左右指针全部都为空，那就是我们的叶子结点
    if(root->_left==NULL&&root->_right==NULL)
    {
        return 1;
    }
//返回我们左子树中的叶子结点和右子树中的叶子结点之和
    return BinaryTreeLeafSize(root->_left)+BinaryTreeLeafSize(root->_right);
}

11.判断是否为完全二叉树

这里我们的主要思路就是通过采取类似层序遍历的方法，找到我们叶子结点的下一层结点。

如果我们的二叉树为一颗完全二叉树，我们叶子结点的下一层结点中的全部结点应该都是null，如果不是的话，就不是完全二叉树。

// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root)
{
//如果我们的根节点是NULL就返回1表示是一棵完全二叉树
    if(root==NULL)
    {
        return 1;
    }
//创建并且初始化我们的队列
    Queue q;
    QueueInit(&q);
//将我们的根节点入队
    QueuePush(&q,root);
//这里与我们层序遍历的思路相同，但是我们需要找到我们层序遍历中的最后一层
//也就是我们叶子结点的下一层
//如果我们的二叉树是一棵完全二叉树，我们的叶子结点的下一层应该全部都是NULL
//在下面的第一个will中我们先找到我们叶子结点的下一层的第一个NULL结点，然后跳出循环
    while(!QueueEmpty(&q))
    {
        BTNode *temp= QueueFront(&q);
        QueuePop(&q);
        if(temp==NULL)
        {
            break;
        }
        QueuePush(&q,temp->_left);
        QueuePush(&q,temp->_right);

    }
//在我们的第二个节点中，我们将继续遍历我们的栈，如果我们当前栈中的全部全部结点都是NULL，
//那我们的二叉树就是完全二叉树，不然就不是
//如果是完全二叉树的话，我们就返回1，不是的话我们就返回0
    while(!QueueEmpty(&q))
    {
        BTNode *temp= QueueFront(&q);
        QueuePop(&q);
        if(temp!=NULL)
        {
            printf("不是完全二叉树\n");
            return 0;
        }
    }
    printf("是完全二叉树\n");
    return 1;
}

对于我们上面所创建的二叉树，我们可以从下面的图中看出，我们经过层次遍历之后，我们找到了叶子结点的下一层结点，当我们读取到null的时候，我们跳出了第一个循环，进入第二个循环，在这第二个循环中，如果我们此时队列中剩余的数据全部都是NULL，我们就能判断这是一棵完全二叉树，但是在下面的图中，我们发现我们在读取到了三个null之后，我们读取到了H这个不为null的值，所以我们可以判断我们当前的这棵二叉树不是完全二叉树。 

 二叉树的实现（C语言数据结构）

 二叉树的实现（C语言数据结构）

12.二叉树的销毁

对于二叉树的销毁，采取后续遍历的形式，先找到我们二叉树中的左子树和右子树中的底层的结点，（这里的底层指的是叶子结点那一层），然后将我们的叶子结点分别释放空间，再一层层返回调用，自下而逐渐销毁。

// 二叉树销毁
void BinaryTreeDestroy(BTNode** root)
{
    if(*root==NULL)
    {
        return;
    }
    BinaryTreeDestroy(&((*root)->_left));
    BinaryTreeDestroy(&((*root)->_right));
    free(*root);
    *root=NULL;
    return;
}

13.求二叉树的高度

int BinaryTreeHeight(BTNode*root)
{
//如果我们的根节点为空的话，我们就直接返回
    if(root==NULL)
    {
        return 0;
    }
//如果我们找到了我们的叶子结点，我们就返回1
    if(root->_right==NULL&&root->_left==NULL)
    {
        return 1;
    }
//递归调用，如果我们的左子树的高度大于右子树的高度，我们返回的数据就是左子树的高度再加1
//这里的+1就是我们当前层的结点
//如果我们的右子树的高度大于我们左子树的高度，我们返回的数据就是右子树的高度再加1
    return (BinaryTreeHeight(root->_left)>=BinaryTreeHeight(root->_right) ? BinaryTreeHeight(root->_left)+1 :BinaryTreeHeight(root->_right)+1);
}

14.汇总

以下是我们写在Btree.c中的全部代码（含有二叉树加上队列的代码）

#include "Btree.h"

BTNode* BuyNode(BTDataType x)
{
    BTNode* node = (BTNode*)malloc(sizeof(BTNode));
    assert(node);

    node->_data = x;
    node->_left = NULL;
    node->_right = NULL;

    return node;
}


BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{
    if(a[*pi] == '#' || *pi >= n)
    {
        printf("NULL ");
        (*pi)++;
        return NULL;
    }
    BTNode *dst= BuyNode(a[*pi]);
    printf("%c ",dst->_data);
    (*pi)++;

    dst->_left = BinaryTreeCreate(a,n,pi);
    dst->_right = BinaryTreeCreate(a,n,pi);

    return dst;
}


//先序遍历
void BinaryTreePrevOrder(BTNode* root)
{
    if(root == NULL)
    {
        return;
    }

    printf("%c ",root->_data);
    BinaryTreePrevOrder(root->_left);
    BinaryTreePrevOrder(root->_right);
}

// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{
    BinaryTreePrevOrder(root->_left);
    if(root == NULL)
    {
        return;
    }

    printf("%c ",root->_data);
    BinaryTreePrevOrder(root->_right);
}

// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{
    BinaryTreePrevOrder(root->_left);
    BinaryTreePrevOrder(root->_right);
    if(root == NULL)
    {
        return;
    }

    printf("%c ",root->_data);
}

// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
    Queue q;
    QueueInit(&q);
    assert(root);
    QueuePush(&q, root);
    while(!QueueEmpty(&q))
    {
        BTNode *temp= QueueFront(&q);
        printf("%c ",temp->_data);
        if(temp->_left)
        {
            QueuePush(&q,temp->_left);
        }
        if(temp->_right)
        {
            QueuePush(&q,temp->_right);
        }

        QueuePop(&q);
    }
    QueueDestory(&q);
}

// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
    if(root==NULL)
    {
        return 0;
    }
    if(root->_left==NULL&&root->_right==NULL)
    {
        return 1;
    }
    return BinaryTreeSize(root->_left)+BinaryTreeSize(root->_right)+1;
}

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
    if(root==NULL)
    {
        return NULL;
    }
    if(root->_data==x)
    {
        return root;
    }
    BinaryTreeFind(root->_left, x);
    BinaryTreeFind(root->_right,x);
}

// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
    if(root==NULL)
    {
        return 0;
    }
    if(k==1)
    {
        return 1;
    }
    return BinaryTreeLevelKSize(root->_left, k-1)+BinaryTreeLevelKSize(root->_right, k-1);
}

// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
    if(root==NULL)
    {
        return 0;
    }
    if(root->_left==NULL&&root->_right==NULL)
    {
        return 1;
    }
    return BinaryTreeLeafSize(root->_left)+BinaryTreeLeafSize(root->_right);
}

// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root)
{
    if(root==NULL)
    {
        return 1;
    }
    Queue q;
    QueueInit(&q);
    QueuePush(&q,root);
    while(!QueueEmpty(&q))
    {
        BTNode *temp= QueueFront(&q);
        QueuePop(&q);
        if(temp==NULL)
        {
            break;
        }
        QueuePush(&q,temp->_left);
        QueuePush(&q,temp->_right);

    }
    while(!QueueEmpty(&q))
    {
        BTNode *temp= QueueFront(&q);
        QueuePop(&q);
        if(temp!=NULL)
        {
            printf("不是完全二叉树\n");
            return 0;
        }
    }
    printf("是完全二叉树\n");
    return 1;
}
// 二叉树销毁
void BinaryTreeDestroy(BTNode** root)
{
    if(root==NULL)
    {
        return ;
    }
    if(*root==NULL)
    {
        return;
    }
    BinaryTreeDestroy(&((*root)->_left));
    BinaryTreeDestroy(&((*root)->_right));
    free(*root);
    *root=NULL;
    return;
}

//求二叉树的高度
int BinaryTreeHeight(BTNode*root)
{
    if(root==NULL)
    {
        return 0;
    }
    if(root->_right==NULL&&root->_left==NULL)
    {
        return 1;
    }
    return (BinaryTreeHeight(root->_left)>=BinaryTreeHeight(root->_right) ? BinaryTreeHeight(root->_left)+1 :BinaryTreeHeight(root->_right)+1);
}

//队列的创建
void QueueInit(Queue* pq)
{
    assert(pq);
    pq->head = pq->tail = NULL;
}

void QueueDestory(Queue* pq)
{
    assert(pq);
    QNode* cur = pq->head;
    while (cur)
    {
        QNode* next = cur->next;
        free(cur);
        cur = next;
    }

    pq->head = pq->tail = NULL;
}

void QueuePush(Queue* pq, QDataType x)
{
    assert(pq);
    QNode* newnode = (QNode*)malloc(sizeof(QNode));
    assert(newnode);

    newnode->data = x;
    newnode->next = NULL;

    if (pq->tail == NULL)
    {
        assert(pq->head == NULL);
        pq->head = pq->tail = newnode;
    }
    else
    {
        pq->tail->next = newnode;
        pq->tail = newnode;
    }
}

void QueuePop(Queue* pq)
{
    assert(pq);
    assert(pq->head && pq->tail);

    if (pq->head->next == NULL)
    {
        free(pq->head);
        pq->head = pq->tail = NULL;
    }
    else
    {
        QNode* next = pq->head->next;
        free(pq->head);
        pq->head = next;
    }
}

bool QueueEmpty(Queue* pq)
{
    assert(pq);

    //return pq->head == NULL && pq->tail == NULL;
    return pq->head == NULL;
}

size_t QueueSize(Queue* pq)
{
    assert(pq);
    QNode* cur = pq->head;
    size_t size = 0;
    while (cur)
    {
        size++;
        cur = cur->next;
    }

    return size;
}

QDataType QueueFront(Queue* pq)
{
    assert(pq);
    assert(pq->head);

    return pq->head->data;
}

QDataType QueueBack(Queue* pq)
{
    assert(pq);
    assert(pq->tail);

    return pq->tail->data;
}

以下是我们写在Btree.h中的全部代码（二叉树再加上队列的代码）

#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>
typedef char BTDataType;

typedef struct BinaryTreeNode
{
    BTDataType _data;
    struct BinaryTreeNode* _left;
    struct BinaryTreeNode* _right;
}BTNode;

BTNode* BuyNode(BTDataType x);

// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);
// 二叉树销毁
void BinaryTreeDestroy(BTNode** root);
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root);
// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root);
//求二叉树的高度
int BinaryTreeHeight(BTNode* root);

typedef BTNode *QDataType;

typedef struct QueueNode
{
    QDataType data;
    struct QueueNode* next;
}QNode;

typedef struct Queue
{
    QNode* head;
    QNode* tail;

    //size_t size;
}Queue;

void QueueInit(Queue* pq);
void QueueDestory(Queue* pq);
void QueuePush(Queue* pq, QDataType x);
void QueuePop(Queue* pq);
bool QueueEmpty(Queue* pq);
size_t QueueSize(Queue* pq);
QDataType QueueFront(Queue* pq);
QDataType QueueBack(Queue* pq);

三、测试代码

以下是我们写在test.c中的代码

#include"Btree.h"
int main() {
    char a[17]={'A','B','D','#','#','E','#','H','#','#','C','F','#','#','G','#','#'};
    int b=0;
    int *pi=&b;
    BTNode *Btree=BinaryTreeCreate(a, 16, pi);
    printf("\n");
//前序遍历
    BinaryTreePrevOrder(Btree);
    printf("\n");
//中序遍历
    BinaryTreeInOrder(Btree);
    printf("\n");
//后序遍历
    BinaryTreePostOrder(Btree);
    printf("\n");
    //乘次遍历
    BinaryTreeLevelOrder(Btree);
    printf("\n");

    int number=BinaryTreeSize(Btree);
    printf("%d",number);
    printf("\n");
    //查找为x的结点
    BTNode *find=BinaryTreeFind(Btree, 'A');
    printf("%c\n",find->_data);

    //查询第k层的结点个数
    int w=BinaryTreeLevelKSize(Btree, 3);
    printf("%d\n",w);

    //查询叶子结点的个数
    int count=BinaryTreeLeafSize(Btree);
    printf("%d\n",count);

//判断当前是否为一棵完全二叉树
    int r=BinaryTreeComplete(Btree);

    //求二叉树的高度
    int x=BinaryTreeHeight(Btree);
    printf("二叉树的高度是%d\n",x);
//    int c=fmax(2,1);
//    printf("%d\n",c);
//销毁二叉树
    BinaryTreeDestroy(&Btree);
    return 0;
}

以下是我们代码的输出结果

​​​​​​​二叉树的实现（C语言数据结构）文章来源地址https://www.toymoban.com/news/detail-440568.html

到了这里，关于二叉树的实现（C语言数据结构）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：
领支付宝红包 赞助服务器费用

相关文章

  • 数据结构入门（C语言版）二叉树的顺序结构及堆的概念及结构实现应用

    数据结构入门（C语言版）二叉树的顺序结构及堆的概念及结构实现应用

    普通的二叉树是不适合用数组来存储的，因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用 顺序结构的数组来存储 ，需要注意的是 这里的堆和操作系统虚拟进程地址空间中的堆是两回事 ，一个是 数据结构 ，一

    2023年04月19日
    浏览(53)
  • 【C语言 数据结构】二叉树的遍历

    【C语言 数据结构】二叉树的遍历

    所谓先序遍历二叉树，指的是从根结点出发，按照以下步骤访问二叉树的每个结点： 访问当前结点； 进入当前结点的左子树，以同样的步骤遍历左子树中的结点； 遍历完当前结点的左子树后，再进入它的右子树，以同样的步骤遍历右子树中的结点； 先序遍历这棵二叉树的过

    2024年02月04日
    浏览(45)
  • 【数据结构】树、二叉树的概念和二叉树的顺序结构及实现

    【数据结构】树、二叉树的概念和二叉树的顺序结构及实现

    之前我们学习了顺序表、链表以及栈和队列这些数据结构，但这些数据结构都是线性的（一对一）。接下来要学习 非线性的数据结构——树（二叉树） ，相比前面的，树的结构更加复杂，话不多说，直接进入正题吧。 树是一种 非线性的数据结构 ，它是 一对多（也有可能是

    2024年02月07日
    浏览(42)
  • 【数据结构—二叉树的链式结构实现】

    【数据结构—二叉树的链式结构实现】

    提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档 文章目录 前言 一、二叉树的存储结构 二、二叉树链式结构的实现 2.1手动构建一课树 2.2二叉树的遍历 三、二叉树链式结构的实现 3.1前序遍历(递归) 3.2中序遍历(递归) 3.3后序遍历(递归) 3.4层序遍历(非递

    2024年02月03日
    浏览(59)
  • 【数据结构 —— 二叉树的链式结构实现】

    【数据结构 —— 二叉树的链式结构实现】

    树是一种非线性的数据结构，它是由n（n=0）个有限结点组成一个具有层次关系的集合。 把它叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。 1.有一个 特殊的结点，称为根结点 ，根节点没有前驱结点 2.除根节点外， 其余结点被分成M(M0)个互不相交

    2024年02月05日
    浏览(57)
  • 【数据结构】二叉树的实现

    【数据结构】二叉树的实现

    一棵二叉树是结点的一个有限集合，该集合分为两点: 一是为空和二是由一个根节点加上两棵别称为左子树和右子树的二叉树组成从图上看出有2个性质： 二叉树不存在度大于2的结点 二叉树的子树有左右之分，次序不能颠倒，因此二叉树是有序树 对于任意的二叉树都是由以下

    2024年02月02日
    浏览(39)
  • 【数据结构】二叉树的链式结构及实现

    【数据结构】二叉树的链式结构及实现

    目录 1. 前置说明 2. 二叉树的遍历 2.1 前序、中序以及后序遍历 2.2 层序遍历 3. 节点个数及高度等 4. 二叉树的创建和销毁 在学习二叉树的基本操作前，需先要创建一棵二叉树，然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入，为了降低大家学习成

    2024年02月08日
    浏览(44)

  • 数据结构：二叉树的链式结构的实现

      目录  1.通过前序遍历构建二叉树 2. 二叉树的销毁  3.二叉树的遍历 4. 二叉树的节点个位和二叉树的叶子节点个位数 5. 二叉树的的k层节点数和查找值为x的节点 6. 判断二叉树是否为完全二叉树和求二叉树的高度h 二叉树的前序遍历 二叉树的中序遍历 二叉树的后序遍历

    2024年02月12日
    浏览(49)
  • 【数据结构】二叉树的顺序结构及实现

    【数据结构】二叉树的顺序结构及实现

    目录 1. 二叉树的顺序结构 2. 堆的概念及结构 3. 堆的实现 3.1 堆向下调整算法 3.2 堆的创建 3.3 建堆时间复杂度 3.4 堆的插入 3.5 堆的删除 3.6 堆的代码实现 4. 堆的应用 4.1 堆排序 4.2 TOP-K问题 普通的二叉树是不适合用数组来存储的，因为可能会存在大量的空间浪费。而完全二叉

    2024年02月08日
    浏览(42)
  • 数据结构实验报告，二叉树的基本操作（C语言）

    数据结构实验报告，二叉树的基本操作（C语言）

    作者：命运之光 专栏：数据结构 实验六 二叉树的基本操作 实验环境：Visual C++或Dev C++ 实验目的： 1、掌握二叉树创建； 2、掌握二叉树的遍历及常用算法。 实验内容： 通过完全前序序列创建一棵二叉树，完成如下功能： 1)输出二叉树的前序遍历序列； 2)输出二叉树的中序遍

    2024年02月09日
    浏览(37)

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

博客赞助

微信扫一扫打赏

请作者喝杯咖啡吧~博客赞助

支付宝扫一扫领取红包，优惠每天领

二维码1

领取红包

二维码2

领红包