三轴机械臂逆运动学解算（附代码）-Toy模板网

这篇具有很好参考价值的文章主要介绍了三轴机械臂逆运动学解算（附代码）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

三轴机械臂逆运动学解算（附代码）

机械臂运动位姿的求解有两种方式

一、正运动学

通过控制已知的连轴（舵机或电机）的旋转角度，求出机械臂终端的空间坐标

二、逆运动学

通过已知的抓取点的空间坐标，求解出三个舵机所需要转动的角度，这里主要讲解逆运动学解法

三轴机械臂逆运动学解算（附代码）

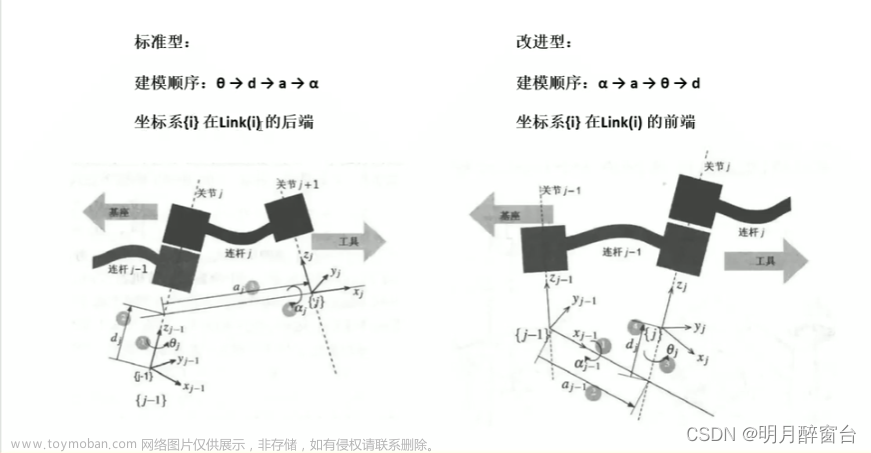
此处θ1 ，θ2， θ3是三个舵机所需转动的角度，γ是杆3相对于x轴的夹角，根据刚体旋转，逆运动学求解，会得到两个解，即有两种姿态，相对于前一个杆逆时针旋转的夹角为正，顺时针为负。如上图第一种姿态（上折线），θ1＜0，θ2<0，θ3＞0

三、求解

（这里就第一种姿态求解）

①求B点坐标

已知空间点A坐标x,y。（因为三杆必然处于同于平面，若涉及z坐标，则机械臂下方云台的解算应考虑在内。

Bx = x - L3*cos(γ);

By = y - L3*sin(γ);

②求出θ1

cosβ = (Bx^2+ By^2 + L1^2 -L2^2) / (2* L1 *sqrt(Bx^2 +By^2));

β = acos(cosβ)*180/pi;

α = atan2(By,Bx)*180/pi;

θ1=－（pi/2-α-β）; //数学上θ1为正，但应用上应为负值

③求出θ2

cosθ2 = (Bx^2 + By^2 - L1^2 - L2^2)/(2* L1 *L2);

θ2 = - acos(cosθ2 )*180/pi； //同理θ2改为负值

④求出θ3（这里的γ需预先定好）

通过γ = θ1 + θ2 + θ3

求出θ3 = γ- θ1- θ2

至此三个角度结算完毕

四、代码实现

#include “stdio.h”
#include “math.h”
float theta[3];
#define pi 3.1415
void caculate(float x, float y, float z, float * ptheta)
{
float L1 = 0.14; //杆长
float L2 = 0.11;
float L3 = 0.04;
Bx=x-L3; //这里设置γ为-90
By=y;
lp=Bx* Bx+By* By;
if (sqrt(lp)>=L1+L2 || sqrt(lp)<=fabs(L1-L2))
printf(“unreached”);
alpha = atan2(By,Bx);
beta = acos((L1* L1+lp-L2* L2)/(2* L1* sqrt(lp))); //这里使用弧度制
ptheta[0] = -(pi/2.0-alpha-beta);
ptheta[1] = acos((L1* L1+L2* L2-lp)/(2* L1 *L2))-pi;
ptheta[2] = -ptheta[0] -ptheta[1]- pi/2;
}

caculate(0.14, 0.09, 0.1, theta);

ROS moveit仿真效果

三轴机械臂逆运动学解算（附代码）
参考博客
(https://blog.csdn.net/xinglucao/article/details/86534402?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522164432010116780261924975%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fblog.%2522%257D&request_id=164432010116780261924975&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2_blogfirst_rank_ecpm_v1~hot_rank-1-86534402.nonecase&utm_term=%E4%B8%89%E8%BD%B4%E6%9C%BA%E6%A2%B0%E8%87%82%E6%8E%A7%E5%88%B6%E7%AE%97%E6%B3%95&spm=1018.2226.3001.4450)

修改：代码中部分 * 没有打出来文章来源地址https://www.toymoban.com/news/detail-440794.html

void caculate(float x, float y, float z, float *ptheta)
{
	float L1 = 0.14; //杆长
	float L2 = 0.11;
	float L3 = 0.04;
	float alpha, beta, lp, Bx, By;
	Bx=x-L3; //这里设置γ为-90
	By=y;
	lp=Bx*Bx+By*By;
	if (sqrt(lp)>=L1+L2 || sqrt(lp)<=fabs(L1-L2))
		return 1;
	alpha = atan2(By,Bx);
	beta = acos((L1*L1+lp-L2*L2)/(2*L1*sqrt(lp))); //这里使用弧度制
	ptheta[0] = -(pi/2.0-alpha-beta);
	ptheta[1] = acos((L1*L1+L2*L2-lp)/(2*L1*L2))-pi;
	ptheta[2] = -ptheta[0] -ptheta[1]- pi/2.0;
	return 0;
}