目录
一、图解向量组的线性相关性
1. 向量组线性相关的定义
2.三维空间中向量组线性相关的几何意义
3.向量组线性相关与齐次线性方程组
二、向量组线性相关的基本结论
三、向量组线性相关性总结
一、图解向量组的线性相关性
1. 向量组线性相关的定义
2.三维空间中向量组线性相关的几何意义
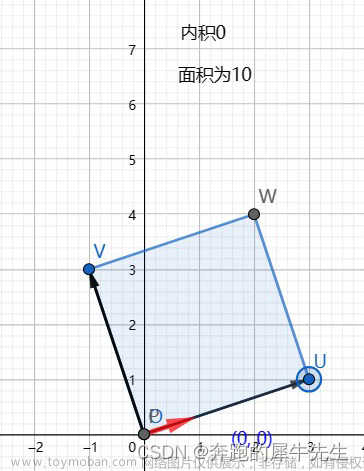
做出向量组A与向量组B的图如下：
旋转图形得到：
旋转后发现，向量组A可以形成一个平面，即向量组A线性相关；
向量组B，不能形成一个平面，即向量组B线性无关；
3.向量组线性相关与齐次线性方程组
向量组线性相关，即齐次线性方程组有非零解。
二、向量组线性相关的基本结论
根据上面的定理：
向量组线性相关的充分必要条件是：R(A)=n
向量组线性无关的充分必要条件是：R(A)<n
做出几何图形如下：
在三维向量空间中，向量组A形成了一个平面，向量组B中的a4位于这个平面之外。
因为给向量组A增加了一个向量得到向量组B，R(A)<=3,R(B)<=3,
又因为向量组A的个数为3，向量组B的个数为4，则有 R(B)<4.
总结如下：
三、向量组线性相关性总结
（1） 两个向量线性相关的充分必要条件是对应分量成比例，几何意义是两向量共线；
（2）三个向量线性相关的几何意义是三向量共面；
（3）向量组线性相关的充分必要条件是R(A)<m,线性无关的充分必要条件是R(A)=m；
（4）向量组线性相关，则就是对应齐次线性方程组有非零解；
（5）m个n维向量组，若m>n，则向量组一定线性相关；文章来源：https://www.toymoban.com/news/detail-441299.html
（6）若向量组线性相关，则向量组线性相关；文章来源地址https://www.toymoban.com/news/detail-441299.html
到了这里，关于【线性代数】向量组的线性相关性的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
