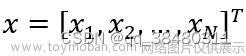作者：aminzeng2022
目录
2. 傅里叶变换
2.1 向量基
2.2 正变换
2.3 反变换
2.4 时域和频域分析
2.5 复数表达式
2.6复指数向量基
2. 傅里叶变换
傅里叶级数也是一组完备的正交向量基（以下简称傅氏向量基），一些连续可积的向量（函数）可以通过向傅氏向量基投影来实现变换，即傅里叶变换。
再次强调，函数也是特殊的向量！连续函数在某个区间可得到无穷个函数值，这些有序值就是一个向量。
2.1 向量基
傅里叶变换的向量基为：
1、cosx、sinx、cos(2x)、sin2x、cos(3x)、sin(3x)、⋯⋯。
傅氏向量基的维数为无穷维，具有正交性、完备性特点，但不具备归一性，进行傅氏变换时应进行归一化处理。
傅氏向量基中的向量为函数，在一个周期内[-π，+π]连续取值，其维数也是无穷维。
- 正交性
在[-π，+π]上，傅氏向量基中任意两个向量的点积都为零，即两两正交，如下：
其中，k、n不相等，取值1、2、3、⋯。
- 归一性
上面提到，傅氏向量基中的向量的大小不为1，如下：
对向量基进行归一化处理，得到归一化后的傅氏向量基为：
、
、
、
、
、
- 完备性
通过对傅里叶变换求极限，可以证明当n→∞时，
所以说明傅氏向量基是完备的，通过傅氏向量基进行变换不存在误差。此证明过程略，感举趣的朋友可以自行在网上查找。
2.2 正变换
变换即是将某个向量从一个坐标系（向量基1）投影到另一个坐标系（向量基2）上得到新的坐标值的过程。
在傅里叶变换中，需变换的向量为函数f(x)，函数定义在x域上，傅氏向量基也定义在x域上，因此可以开展投影操作。向量f(x)在傅氏向量基上的投影值依次为：
对
投影：
对
投影：
对
投影：
所以傅立叶变换为：
简化后得到：
其中系数：
所以f(x)在傅氏向量基上的坐标为：
2.3 反变换
根据图1.7知道，进行反变换要捋清两组向量基（坐标系）之间的关系和坐标值，设向量g在原坐标系向量基中表示为f(x)，即g= f(x)，正反变换分析如下：
- 正变换：傅里叶变换，将向量g在原坐标系中的坐标值（f(x)）投影在傅氏向量基（在原坐标系中表示为1、cosx、sinx、⋯⋯），得到向量g在傅氏向量基中的坐标值（a0、a1、b1、⋯⋯）；
- 反变换：傅里叶逆变换，将向量g在傅氏向量基中的坐标值（a0、a1、b1、⋯⋯）投影在原坐标系向量基（在傅氏向量基中表示为1、cosx、sinx、⋯⋯），得到向量g在原坐标系中的坐标值（f(x)）。
理解的难点就在于“原坐标系向量基在傅氏向量基中表示为1、cosx、sinx、⋯⋯”。理解如下：
- 因为g在原坐标系向量基中表示为f(x)，即g= f(x)，也即g= f(x)∙1，坐标值是f(x)，所以1就是向量基；
- 原坐标系向量基1投影到傅氏向量基上，得到1、cosx、sinx、⋯⋯；
- 所以原坐标系向量基在傅氏向量基上的坐标值也为1、cosx、sinx、⋯⋯，与傅氏向量基在原坐标系上的表达式相同。
所以傅里叶反变换为：
傅里叶正反变换的表达形式好像是一样的，但其实不同，正变换是求坐标值a0、a1、b1等，而反变换是求f(x)，这一点不分清容易搞蒙。
2.4 时域和频域分析
向量g= f(x)是在x域上的表达式，若令x(x=ωt)表示时间，那就是时间域上的表达式，向量
，为表达简洁，还是令g= f(t)。
设向量周期为T，角频率为ω=2π/T，因x∈[-π,+π]，所以t∈[-T/2,+T/2]，对傅氏坐标值进行适当变换后得到：
得到傅里叶变换为：
对上式进行解读：
- f(t)表示一个周期信号随时间变化的函数；
-
为一个常数； - cosnωt为一个余弦信号，角频率为nω，角频率是原函数的n倍；
- sinnωt为一个正弦信号，角频率为nω，角频率是原函数的n倍；
- 傅里叶变换将一个周期信号分解为：常量(a0)+ a1×余弦信号（1倍频）+ b1×正弦信号（1倍频）+ a2×余弦信号（2倍频）+ b2×正弦信号（2倍频）+⋯⋯；
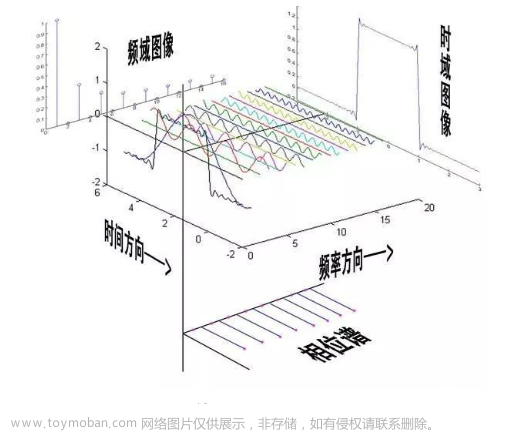
通过信号分解，可看出原信号中所含不同频率正余弦信号的比重（见图2.1），这在信号处理、控制等各领域应用十分广泛。本文目的只是帮助理解傅氏变换，对此不作深入分析。
图2.1 傅里叶时域频域分析示意（图片来自网络）
2.5 复数表达式
为提高傅氏变换的普适性，利用了欧拉公式对傅氏变换进行变形。
欧拉公式：
代入傅氏变换得：
因
和
对称，在-∞~+∞求和得到：
再将欧拉公式代入坐标值求解得到变换系数：
所以可以将
统一为如下形式：
若将T→∞，上式可运用于非周期函数，此时：
令：
该表达式用于求信号当中不同频率的分量，是傅里叶正变换。
将
代入
得到：
该表达式用于根据频率分量求信号时间域表达式，是傅里叶反变换。
2.6复指数向量基
回过头看表达式
，是否很像函数向量
在向量基
上的投影，真实情况也确实如此。
复指数向量基：
⋯⋯、
、
、
、
、
、
、
、⋯⋯
简写为
，n为整数，特别注意n取值范围是-∞~+∞，若只取正整数就不具有完备性了。
- 正交性
证明复指数向量基正交性之前，需将根深蒂固的实数域概念扩展到复数域，以前的实数可看成虚部为零的复数。复数的投影（也就是复数的内积运算）跟实数有较大差异，具体如下：
复数z1：z1=a1+b1i；
共轭复数
：
；
复数z2：
；
共轭复数
：
复数z1和z2的内积为：
若复数z1和z2正交（垂直），则：
；
复指数
的共轭复数
：
下面证明复指数的正交性：
复指数的向量内积：
当m≠n时：
当m=n时：
所以复指数向量基是两两正交的。
- 归一化
复数向量的大小也称为模，计算方法如下：
所以复指数向量基的大小为：
归一化后得到复指数向量基：
⋯⋯、
、
、
、
、
、
、
、⋯⋯
- 完备性
因复指数向量基
与傅氏向量基是对应的，所以复指数向量基也是完备的。
完备性证明省略。
- 正变换
正变换是求每个向量基的投影分量。
频率为nω项：
所以：
当T→∞时：
- 反变换
将所有频率项加在一起，就可得到时域函数向量，但要注意向量基应是时域向量基（=1）在复指数向量基上的表示。
将1依次向复指数向量基投影（求内积）得到：
在n>0时：
在n<0时：
两部分加在一起后再加上n=0的项，就得到：
当T→∞时，频率分辨率很小，用dω表示，写成积分形式：文章来源：https://www.toymoban.com/news/detail-441449.html
文章来源地址https://www.toymoban.com/news/detail-441449.html
到了这里，关于从根上彻底理解各种变换之二：傅里叶变换的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
