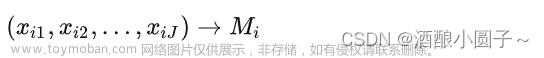【建模算法】熵权法(Python实现)
熵权法是通过寻找数据本身的规律来赋权重的一种方法。
熵是热力学单位,在数学中,信息熵表示事件所包含的信息量的期望。根据定义,对于某项指标,可以用熵值来判断某个指标的离散程度,其熵值越小,指标的离散程度越大,该指标对综合评价的影响(权重)越大。
熵本源于热力学,后由申农(C. E. Shannon)引入信息论,根据熵的定义与原理,当系统可能处于几种不同状态,每种状态出现的概率为
p
i
(
i
=
1
,
2
,
.
.
.
,
m
)
p_i(i=1,2,...,m)
pi(i=1,2,...,m),则该系统的熵就可定义
e
=
−
1
l
n
m
∑
i
=
1
m
p
i
l
n
p
i
.
e=-\frac{1}{lnm}\sum^m_{i=1}p_ilnp_i.
e=−lnm1i=1∑mpilnpi.
熵权法是一种客观赋权方法。在具体使用过程中,熵权法根据各指标的变异程度,利用信息熵计算出各指标的熵权,从而得出较为客观的指标权重。
一、问题描述
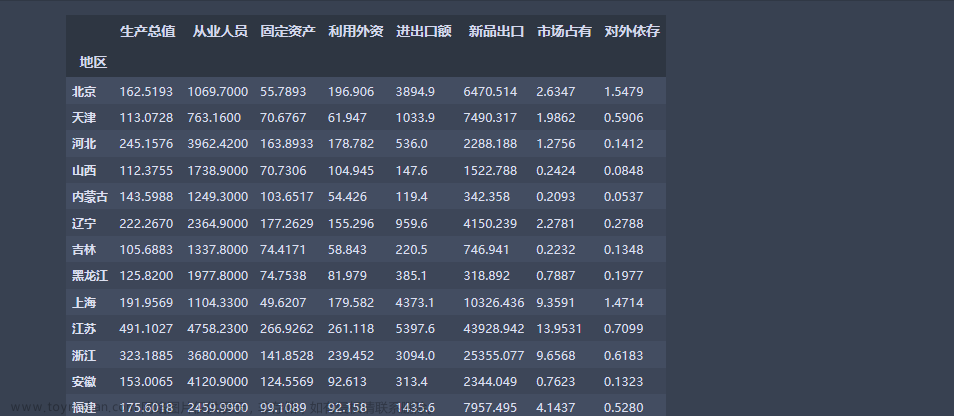
请根据下表给出的10个学生8门课的成绩,给出这10个学生评奖学金的评分排序。
表1:学生成绩表
二、熵权法的评价步骤
设有 n n n个评价对象, m m m个评价指标变量,第 i i i个评价对象关于第 j j j个指标变量的取值为 a i j ( i = 1 , 2 , . . , n ; j = 1 , 2 , . . , m ) a_{ij}(i=1,2,..,n;j=1,2,..,m) aij(i=1,2,..,n;j=1,2,..,m),构造数据矩阵 A = ( a i j ) n × m A=(a_{ij})_{n\times m} A=(aij)n×m。
基于熵权法的评价方法步骤如下:
(1)利用原始数据矩阵
A
=
(
a
i
j
)
n
×
m
A=(a_{ij})_{n\times m}
A=(aij)n×m计算
p
i
j
(
i
=
1
,
2
,
.
.
.
,
n
,
j
=
1
,
2
,
.
.
.
,
m
)
p_{ij}(i=1,2,...,n,j=1,2,...,m)
pij(i=1,2,...,n,j=1,2,...,m),即第
i
i
i个评价对象关于第
j
j
j个指标值的比重
P
i
j
=
a
i
j
∑
i
=
1
n
a
i
j
,
i
=
1
,
2
,
.
.
.
,
n
,
j
=
1
,
2
,
.
.
.
,
m
P_{ij}=\frac{a_{ij}}{\sum^n_{i=1}a_{ij}},i=1,2,...,n,j=1,2,...,m
Pij=∑i=1naijaij,i=1,2,...,n,j=1,2,...,m
(2)计算第
j
j
j项指标的熵值
e
j
=
−
1
l
n
n
∑
i
=
1
1
P
i
j
l
n
P
i
j
,
j
=
1
,
2
,
.
.
.
,
m
e_j=-\frac{1}{lnn}\sum^{1}_{i=1}P_{ij}lnP_{ij},j=1,2,...,m
ej=−lnn1i=1∑1PijlnPij,j=1,2,...,m
(3)计算第
j
j
j项指标的变异系数
g
j
=
1
−
e
j
,
j
=
1
,
2
,
.
.
.
,
m
g_j=1-e_j,j=1,2,...,m
gj=1−ej,j=1,2,...,m
对于第
j
j
j项指标,
e
j
e_j
ej越大,指标值的变异程度就越小。
(4)计算第
j
j
j项指标的权重
w
j
=
g
j
∑
j
=
1
m
g
j
,
j
=
1
,
2
,
.
.
.
,
m
w_j=\frac{g_j}{\displaystyle \sum^m_{j=1}g_j},j=1,2,...,m
wj=j=1∑mgjgj,j=1,2,...,m
(5)计算第
i
i
i个评价对象的综合评价值
F
i
=
∑
j
=
1
m
w
j
p
i
j
F_i=\sum^m_{j=1}w_jp_{ij}
Fi=j=1∑mwjpij
评价值越大越好。文章来源:https://www.toymoban.com/news/detail-441703.html
三、求解结果
指标变量
x
1
、
x
2
、
.
.
.
、
x
8
x_1、x_2、...、x_8
x1、x2、...、x8分别表示学生的语文、数学、物理、化学、英语、政治、生物、历史成绩。用
a
i
j
a_{ij}
aij表示第
i
i
i个学生关于指标变量
x
j
x_j
xj的取值,构造数据矩阵
A
=
(
a
i
j
)
10
×
8
A=(a_{ij})_{10\times 8}
A=(aij)10×8。
利用Python程序,求得的各指标变量的权重值见表2,各个学生的综合评价值及排名次序见表3。各个学生评价值从高到低的次序为:
9 1 3 7 6 5 4 10 8 2.文章来源地址https://www.toymoban.com/news/detail-441703.html
表2:各指标的评价权重表3 :学生的综合评价值及排名次序 运行结果: 四、实现代码
#完整代码:
import numpy as np
import pandas as pd
data = pd.read_excel('stu_data.xlsx') #读取原始数据
label_need=data.keys()[1:]
df=data[label_need]
a=np.array(df)
[n, m]=a.shape
cs=a.sum(axis=0) #逐列求和
P=1/cs*a #求特征比重矩阵
e=-(P*np.log(P)).sum(axis=0)/np.log(n) #计算熵值
g=1-e #计算差异系数
w = g / sum(g) #计算权重
F = P @ w #计算各对象的评价值
print("\nP={}\ne={}\ng={}\nw={}\nF={}".format(P,e,g,w,F))
print('各个学生评价值从高到低的次序为:')
print(np.argsort(-F)+1)
到了这里,关于【建模算法】熵权法(Python实现)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!