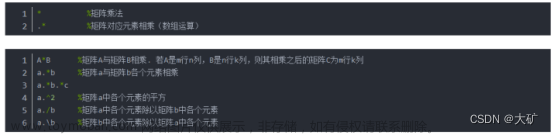
在学习矩阵有关运算的时候要相信自己已经知道了很多线代知识,不然会看不懂的QAQ~
1. 关于矩阵的一些基本运算函数:



例1:生成一个3阶全1矩阵。
>> ones(3)
ans =
1 1 1
1 1 1
1 1 1
例2:产生一个在区间[5,15]内均匀分布的5阶随机矩阵
>> a=5;b=15;
>> x=a+-(b-a)*rand(5)
x =
4.0246 3.4239 3.5811 -1.5574 -2.5774
2.2150 -4.7059 0.7824 4.6429 -2.4313
-0.4688 -4.5717 -4.1574 -3.4913 1.0777
-4.5751 0.1462 -2.9221 -4.3399 -1.5548
-4.6489 -3.0028 -4.5949 -1.7874 3.2881例3:产生均值为0.5,方差为0.3的4阶矩阵
>> mu=0.5; sigma=0.3;
>> x=mu+sqrt(sigma)*randn(3)
x =
0.9866 0.0566 0.6781
-0.1283 -1.1127 0.0865
-0.0854 1.2878 1.2505例4:生成从10到100间具有5个元素的线性等分向量。
>> A= linspace(10,100,5)
A =
10.0000 32.5000 55.0000 77.5000 100.0000例5:生成1到100间的共有10个元素的对数等分向量。
>> L=logspace(0,2,10)
L =
列 1 至 5
1.0000 1.6681 2.7826 4.6416 7.7426
列 6 至 10
12.9155 21.5443 35.9381 59.9484 100.0000例6:生成以143257为对角线的六阶矩阵
>> D=blkdiag(1, 4, 3, 2, 5, 7)
D =
1 0 0 0 0 0
0 4 0 0 0 0
0 0 3 0 0 0
0 0 0 2 0 0
0 0 0 0 5 0
0 0 0 0 0 72. 关于向量的范数norm
例7:求向量X =[1.2,6,3,2]的欧几里德范数,无穷大范数和1-范数。
X=[1,2,6,3,2];
Ml=norm(X)
M2=norm(X,inf)
M3=norm(X,1)
Ml =
7.3485
M2 =
6
M3 =
143. 关于矩阵的范数

4. 矩阵的其它有关运算
包括矩阵的特征值、特征向量、矩阵初等变换的实现、向量组线性相关性的判定、矩阵条件数的计算、矩阵的LU分解等内容。
例8:

1)求解矩阵方程XA=B中的解矩阵,将结果存放在变量X8中;
2)求满足方程组AX=b’的解向量,将结果存放在变量X9中;
3)求X8的特征值和特征向量,将特征向量组存放在变量X10中,相应的特征值记为D;
A = [3 4 -1 -9 10;6 5 0 4 -16;1 -4 7 6 -8;2 -4 5 12 -8;-3 6 -7 -1 1]
B = [1 2 6 -3 2;7 9 -5 8 -7;8 11 1 5 5;10 15 13 -1 9;2 4 -3 0 5]
b = [1 3 5 7 9]
X8=B/A
X9=A\b'
[X10,D]=eig(X8)
>> sy13
A =
3 4 -1 -9 10
6 5 0 4 -16
1 -4 7 6 -8
2 -4 5 12 -8
-3 6 -7 -1 1
B =
1 2 6 -3 2
7 9 -5 8 -7
8 11 1 5 5
10 15 13 -1 9
2 4 -3 0 5
b =
1 3 5 7 9
X8 =
1.2848 -0.2581 2.2305 -0.2302 1.0254
0.8710 0.7178 -1.0437 1.6637 0.7345
2.9196 -0.0074 1.0354 2.2656 2.0937
5.4893 -0.5235 5.4964 1.8053 4.1445
0.7045 -0.0029 -0.5019 0.8143 0.4076
X9 =
-1.8146
3.9184
2.7357
1.5477
0.7435
X10 =
-0.1775 -0.4501 -0.0342 -0.4995 0.0405
-0.1929 0.4921 0.9661 -0.2857 0.2215
-0.4782 0.4877 0.1901 -0.1214 0.3982
-0.8331 -0.4125 0.1218 -0.0479 0.4792
-0.0928 0.3838 -0.1203 0.8074 -0.7490
D =
6.4699 0 0 0 0
0 -1.9352 0 0 0
0 0 0.5999 0 0
0 0 0 -0.0000 0
0 0 0 0 0.1163例9:利用上题的条件:文章来源:https://www.toymoban.com/news/detail-441894.html
1)生成矩阵A的行向量组:a1,a2,a3,a4,a5;
2)由A的1、3、5行,2、4列交叉点上的元素生成A的子矩阵A3;
3)生成一个10阶矩阵A4,其左上角为A,右上角为5阶单位阵,左下角为5阶零矩阵,右下角为B;
4)将A对应的行向量组正交规范化为正交向量组A5,并验证所得结果;
5)完成以下初等变换:将A的第一、四行互换,再将其第三列乘以6;
6)求B的列向量组的一个极大无关向量组A9。
7) 求矩阵A的欧几里德范数,2条件数文章来源地址https://www.toymoban.com/news/detail-441894.html
a1=A(1,:)
a2=A(2,:)
a3=A(3,:)
a4=A(4,:)
a5=A(5,:)
A3=[A(1,2),A(1,4);A(3,2),A(3,4);A(5,2),A(5,4)]
A4=[A,ones(5);zeros(5),B]
A5=orth(A)
Q=A5'*A5
A8=A;
A8([1,4],:)=A8([4,1],:)
A8(:,3)=6*A8(:,3)
A9=rref(B)
n1=norm(A)
n2=cond(A)
>> sy22
A =
3 4 -1 -9 10
6 5 0 4 -16
1 -4 7 6 -8
2 -4 5 12 -8
-3 6 -7 -1 1
B =
1 2 6 -3 2
7 9 -5 8 -7
8 11 1 5 5
10 15 13 -1 9
2 4 -3 0 5
b =
1 3 5 7 9
a1 =
3 4 -1 -9 10
a2 =
6 5 0 4 -16
a3 =
1 -4 7 6 -8
a4 =
2 -4 5 12 -8
a5 =
-3 6 -7 -1 1
A3 =
4 -9
-4 6
6 -1
A4 =
3 4 -1 -9 10 1 1 1 1 1
6 5 0 4 -16 1 1 1 1 1
1 -4 7 6 -8 1 1 1 1 1
2 -4 5 12 -8 1 1 1 1 1
-3 6 -7 -1 1 1 1 1 1 1
0 0 0 0 0 1 2 6 -3 2
0 0 0 0 0 7 9 -5 8 -7
0 0 0 0 0 8 11 1 5 5
0 0 0 0 0 10 15 13 -1 9
0 0 0 0 0 2 4 -3 0 5
A5 =
0.4724 0.1034 -0.6304 -0.5125 0.3258
-0.5201 0.7742 -0.3367 0.0090 -0.1291
-0.4335 -0.2709 -0.2367 0.3210 0.7613
-0.5408 -0.2940 0.1538 -0.7719 -0.0392
0.1613 0.4797 0.6399 -0.1958 0.5441
Q =
1.0000 0.0000 0.0000 0.0000 0.0000
0.0000 1.0000 -0.0000 -0.0000 -0.0000
0.0000 -0.0000 1.0000 0.0000 -0.0000
0.0000 -0.0000 0.0000 1.0000 0.0000
0.0000 -0.0000 -0.0000 0.0000 1.0000
A8 =
2 -4 5 12 -8
6 5 0 4 -16
1 -4 7 6 -8
3 4 -1 -9 10
-3 6 -7 -1 1
A8 =
2 -4 30 12 -8
6 5 0 4 -16
1 -4 42 6 -8
3 4 -6 -9 10
-3 6 -42 -1 1
A9 =
1.0000 0 0 3.4800 0
0 1.0000 0 -2.0400 0
0 0 1.0000 -0.4000 0
0 0 0 0 1.0000
0 0 0 0 0
n1 =
27.7254
n2 =
17.0546到了这里,关于matlab基础(一):matlab中矩阵的基本运算的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!