统计子矩阵（前缀和+双指针）-Toy模板网

这篇具有很好参考价值的文章主要介绍了统计子矩阵（前缀和+双指针）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

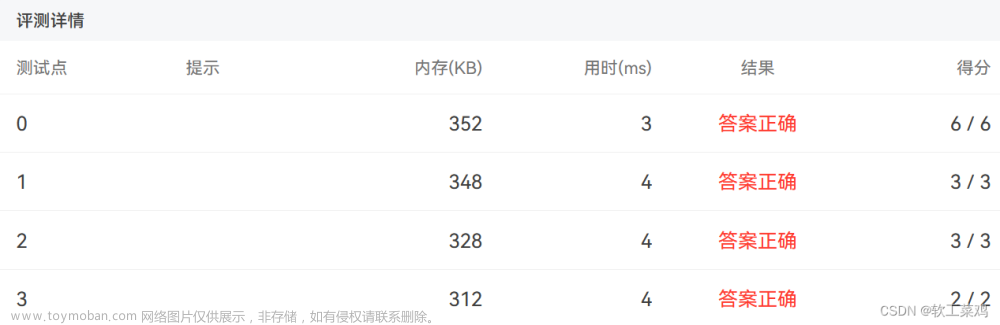
给定一个 N × M 的矩阵A，请你统计有多少个子矩阵(最小 1 × 1，最大 N × M) 满足：
子矩阵中所有数的和不超过给定的整数K?

输入格式

第一行包含三个整数N, M 和K.
之后 N 行每行包含 M 个整数，代表矩阵A.
30%的测试数据：1≤N,M≤20；
70%的测试数据：1≤N,M≤100；
100%的测试数据：1≤N,M≤500；0≤Aij≤1000；1≤K≤250000000。

输出格式

一个整数代表答案。

输入样例

输出样例

数据范围与提示

满足条件的子矩阵一共有19，包含：
大小为1 × 1 的有10 个。
大小为1 × 2 的有3 个。
大小为1 × 3 的有2 个。
大小为1 × 4 的有1 个。
大小为2 × 1 的有3 个。

解析：

二维前缀和，但是枚举所有情况时间复杂度为O（n^4），所以我们先枚举左右边界，然后双指针枚举上下边界。

因为枚举上下边界（左右也可以），存在单调性。

代码： 文章来源地址https://www.toymoban.com/news/detail-442312.html

#include<bits/stdc++.h>
using namespace std;
const int N=500+5;
int n,m,k,a[N][N],sum[N][N];
int main(){
    scanf("%d%d%d",&n,&m,&k);
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            scanf("%d",&a[i][j]);
            sum[i][j]=sum[i-1][j]+sum[i][j-1]+a[i][j]-sum[i-1][j-1];
        }
    }
    long long res=0;
    for(int i=1;i<=m;i++){
        for(int j=i;j<=m;j++){
        	for(int t=1,s=1;t<=n;t++){
        		while(s<=t&&sum[t][j]-sum[s-1][j]-sum[t][i-1]+sum[s-1][i-1]>k) s++;
        		if(s<=t) res+=t-s+1;
			}
        }
    }
    cout<<res;
    return 0;
}

到了这里，关于统计子矩阵（前缀和+双指针）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！