求无向图的最小生成树——Kruskal算法（超详细）【并查集，python实现】-Toy模板网

这篇具有很好参考价值的文章主要介绍了求无向图的最小生成树——Kruskal算法（超详细）【并查集，python实现】。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、题目

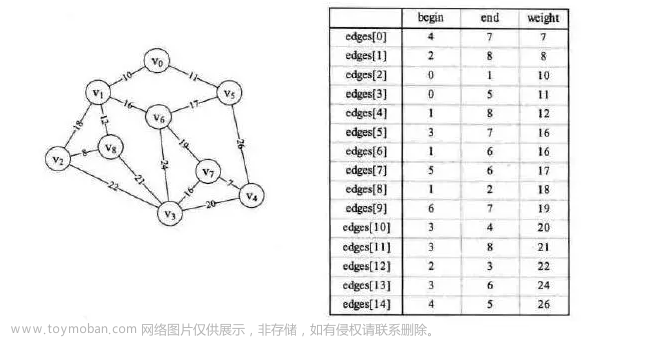
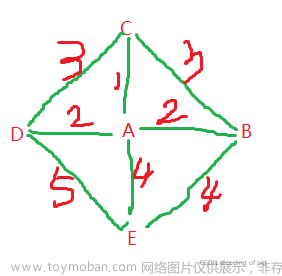
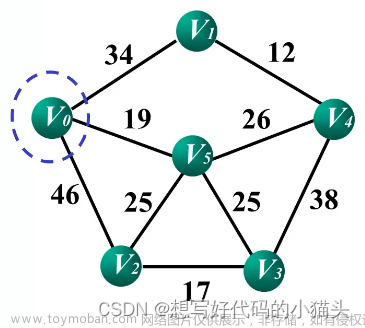
以如下无向图为例，求最小生成树及其权值。求无向图的最小生成树——Kruskal算法（超详细）【并查集，python实现】
补充知识点：
最小生成树（不官方的解释）：包含所有节点，保持整个图连通，所有边权值之和最小。

二、思路

1、补充在前

（1）图的存储

采用二维列表存储（点，点，边的权值）

# 由图我们得到的信息
edges = [['A', 'B', 2], ['A', 'D', 5], ['A', 'F', 8],
         ['B', 'C', 7], ['B', 'D', 7], ['B', 'E', 2],
         ['C', 'E', 3], ['D', 'E', 6], ['D', 'F', 7],
         ['D', 'G', 3], ['E', 'G', 4], ['F', 'G', 4]]

（2）顶点转换

为了便于计算，将字母A ~ G用数字0 ~ 6代替（这里可以使用字典实现）

# 字典key:value值
di = {0: 'A', 1: 'B', 2: 'C', 3: 'D', 4: 'E', 5: 'F', 6: 'G'}
# 顶点和边的关系转换如下
edges = [[0, 1, 2], [0, 3, 5], [0, 5, 8],
         [1, 2, 7], [1, 3, 7], [1, 4, 2],
         [2, 4, 3], [3, 4, 6], [3, 5, 7],
         [3, 6, 3], [4, 6, 4], [5, 6, 4]]

2、Kruskal算法思想

【画出所有节点（n 个），不加边】—> 【将边按权值由小到大排列】—> 【依次加上每一条边，判断加上该边后是否形成闭环，若形成闭环，则去掉该边；若不形成，则不动，继续下一条边的判断，直到图中一共加了 n - 1 条边，结束】
那么我们该怎么判断加上一条边后是否形成闭环呢？
画图我们很容易看出有没有形成闭环，重点是怎么利用代码实现这个过程，这就要用到下面的并查集了（说实话，我第一次遇到并查集这个概念的时候是很懵的，记得当时搞了好久才把这个思路理清楚，过程曲折且痛苦。。。）

3、并查集模板

（1）初始化父节点

初始化每一个顶点的父节点都自己（因为最开始一条边都还没有加上的时候，每一个顶点之间还没有联系）`

# 初始化n个节点的 fa（父节点）
# 这里的下划线和变量 i 同理
fa = [_ for _ in range(n)]

（2）查询父节点——查

# 查找当前元素所在树的根节点(代表元素)
def found(node):
	# 如果父节点就是自己，代表已经找到，直接返回即可
    if fa[node] == node:
        return node
    else:
        # 如果父节点不是自己，那就往上找一层，找父节点的父节点
        # 递归下去一定能找到
        fa[node] = found(fa[node])
        return fa[node]

（3）合并两节点所在集合——并

# 合并元素 node1, node2 所处的集合
def unite(node1, node2):
	# 先找两个节点的父节点
    node1 = found(node1)
    node1 = found(node1)
    # 如果父节点都一样，说明已经在一个集合中，不能再合并了
    if node1 == node2:
        return False
    else:
        # 统一两顶点的父节点，能合并
        fa[node1] = node2
        return True

三、完整实现及结果

def Kruskal(n, m, edges):
    # 按边权值排序
    edges.sort(key=lambda edges: int(edges[2]))

    # 初始化边数和放置边数的集合
    edge_num = 0
    res = []

    # 遍历每一条边
    for i in range(m):

        # 先判断，边数 = n - 1 就结束
        if edge_num == n - 1:
            break

        # 判断能否合并（能合并，证明不成环）
        if unite(edges[i][0], edges[i][1]):
            res.append(edges[i])
        edge_num += 1
    return res


# 查找当前元素所在树的根节点(代表元素)
def found(node):
    if fa[node] == node:
        return node
    else:
        fa[node] = found(fa[node])
        return fa[node]


# 合并元素 node1, node2 所处的集合
def unite(node1, node2):
    node1 = found(node1)
    node1 = found(node1)
    if node1 == node2:
        return False
    else:
        fa[node1] = node2
        return True


m = 12  # 边数
n = 7  # 顶点个数
di = {0: 'A', 1: 'B', 2: 'C', 3: 'D', 4: 'E', 5: 'F', 6: 'G'}

fa = [_ for _ in range(n)]

# 顶点和边的关系
edges = [[0, 1, 2], [0, 3, 5], [0, 5, 8],
         [1, 2, 7], [1, 3, 7], [1, 4, 2],
         [2, 4, 3], [3, 4, 6], [3, 5, 7],
         [3, 6, 3], [4, 6, 4], [5, 6, 4]]
res = Kruskal(n, m, edges)
# 打印最终点边关系
s = 0
for edge in res:
	# 这里箭头只代表两顶点之间的连接作用，与方向无关
    print(f'{di[edge[0]]}->{di[edge[1]]}: {edge[2]}')
    s += edge[2]
print(f'权值：{s}')