R语言的的矩阵相乘 %% 和的区别

9月前作者：cchendd 分类：Toy博客阅读(30) 违法举报

这篇具有很好参考价值的文章主要介绍了R语言的的矩阵相乘 %*% 和 *的区别。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

R语言的的矩阵相乘 %% 和的区别

   想搞明白矩阵相乘%*% 和*的计算原理

一.*的计算原理

①创建1个矩阵test1和1个向量test2
R语言的的矩阵相乘 %*% 和 *的区别

test1*test2

是不是感觉很乱，看不出来是怎么计算的，如果改变一下test1，然后test1*test2

②通过对比上述2种情形，我们可以发现*的计算方式就是先把test1转换为1维向量，然后在乘以test2,即：
R语言的的矩阵相乘 %*% 和 *的区别

二.%*% 的计算原理（矩阵相乘）

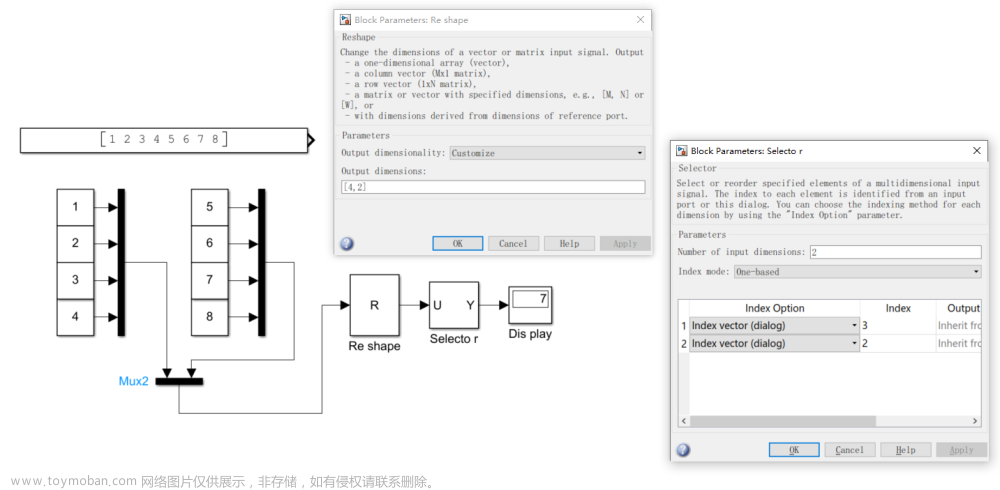
创建2个矩阵test1和test2
R语言的的矩阵相乘 %*% 和 *的区别

4x2矩阵乘以2x1矩阵得到一个4x1矩阵，符合矩阵相乘结果

若对test1做一下调整

2x4矩阵和2x1矩阵无法相乘

总结：

①*类似于在向量上进行运算，不用考虑数据的结构；
②%*%严格按照矩阵相乘的运算法则运行。文章来源地址https://www.toymoban.com/news/detail-443047.html

到了这里，关于R语言的的矩阵相乘 %*% 和 *的区别的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：

领支付宝红包赞助服务器费用

动态规划--矩阵链相乘问题

明确原始问题A[1:n]：计算矩阵链所需的最小乘法次数。（1）是否满足最优子结构，问题的解是否包含子问题的优化解？若计算A[1:n]的优化顺序在 k 处断开矩阵链，即A[1:n]=A[1:k]×A[k+1:n],则在A[1:n]的优化顺序中，对应于子问题A[1:k]的解必须是A[1:k]的优化解，对应A[k+1:n]的解必

2024年01月25日
浏览(41)
14-矩阵相乘及其运算法则

矩阵与向量的乘法在这一篇文章中我们就将基于上一篇重新审视矩阵的这个视点来理解矩阵的乘法，那么在这一篇，我们主要来看一下矩阵和向量的乘法。这里这个线性方程组是上一小节给大家举的模拟的一个非常简单的小型经济系统的例子，我们可以把这个经济系统其实本

2024年02月13日
浏览(39)
矩阵和向量如何相乘？

矩阵与向量相乘遵循特定的数学规则，这个过程通常被称为矩阵向量乘法。在进行矩阵向量乘法时，矩阵的列数必须与向量的行数相同。以下是一个具体的例子：例子：假设我们有一个矩阵 A 和一个向量 v，其中：在这个例子中，矩阵 A 是一个 3x2 矩阵（3行2列），向量v 是

2024年01月22日
浏览(44)
矩阵链相乘（动态规划法）

矩阵链乘法是耳熟能详的问题了，有很多矩阵，排列成矩阵链，矩阵链的要求是相邻的两个是可以相乘的，可以相乘是有条件的，两个矩阵能够相乘的条件就是行、列之间是有关系的，两个矩阵如果能够相乘，就是前面矩阵的列号和后面矩阵的行号是一致的。如何确定矩阵的

2024年02月09日
浏览(48)
矩阵与对角阵相乘的一般特点

矩阵与对角阵相乘的一般特点用对角阵左乘一个矩阵，就是用对角阵的对角元分别乘这个矩阵的对应各行；用对角阵右乘一个矩阵，就是用对角阵的对角元分别乘这个矩阵的对应各列。只有对角线上有非0元素的矩阵称为对角矩阵，或说若一个方阵除了主对角线上的元素外，

2024年02月11日
浏览(30)
矩阵链相乘的乘法次数（动态规划）

该题是算法动态规划练习题该题首先要清楚地认识和理解题意首先，理解一次矩阵乘法会产生多少次乘法运算例如给定两个矩阵（10 * 5）与（5 * 20）会产生的乘法次数为 10*5*20=1000次然后我们要理解当存在多个矩阵相乘时，乘的顺序不同，最终乘法运算的总次数也是不同的

2024年01月25日
浏览(37)
算法导论【分治思想】—大数乘法、矩阵相乘、残缺棋盘

在分而治之的方法中，一个问题被划分为较小的问题，然后较小的问题被独立地解决，最后较小问题的解决方案被组合成一个大问题的解决。通常，分治算法有三个部分：分解：将问题划分为若干子问题，这些子问题是同一问题的较小实例。解决：通过递归地解决子问题来

2024年02月03日
浏览(35)
【SIMULINK】simulink实现信号矩阵整合、求逆、转置、分解、向量矩阵相乘（非matlab）

simulink实现信号矩阵，并实现分解 simulink实现信号矩阵求逆 simulink实现信号矩阵转置 simulink矩阵向量相乘

2024年02月11日
浏览(41)
【Python】如何用 python 计算矩阵相乘 - numpy.dot()

使用 Numpy 包里的 dot() 函数。该函数主要功能有两个：向量点积和矩阵乘法。格式： x.dot(y) 等价于 np.dot(x,y) x 是m × n 矩阵，y 是 n×m 矩阵，则 x.dot(y) 得到 m×m 矩阵。向量相乘，得到内积输出结果：矩阵相乘，得到矩阵的积（1）实例 1 输出结果：（2）实例 2 输出结果

2024年02月11日
浏览(37)
证明矩阵二范数的平方等于转置矩阵与原矩阵相乘后的二范数

定理：对于任意的矩阵 A ∈ R n × m A in R^{ntimes m} A ∈ R n × m ，有 ∥ A ∥ 2 2 = ∥ A T A ∥ 2 left|Aright|_2^2=left|A^TAright|_2 ∥ A ∥ 2 2 = A T A 2 证明：假设矩阵 A T A A^TA A T A 最大特征值为 λ lambda λ ，即 ∥ A ∥ 2 2 = λ left|Aright|_2^2=lambda ∥ A ∥ 2 2 = λ ，设

2024年02月05日
浏览(35)