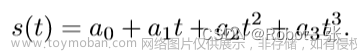1.多项式的定义:
形如 f(x)= an*x^n+.......ai*x^i+...a0 ,叫做多项式,其中ai 是系数,x 是未知数,i 叫做 指数。
若an 不为0称f(x)位 n 次多项式,记作 deg f(x)
如果 a0 !=0,且 ai ==0 (i=1.2....n)则称f(x)为零次多项式,f(x)=b;等同于K 中非零元
规定 0 多项式 的次数,deg0 = -INF ;
deg(f(x)+g(x))=max(degf(x),deg g(x));
deg(f(x)*g(x)) =degf(x)+deg g(x);
多项式加法满足结合律、交换律,多项式乘法满足交换律与结合律。
2.环的定义。
定义一个非空集合R,如果有两个代数运算,加法与乘法。
那么 a, b 是集合中的两个元。
且 满足加法与乘法,结合律,交换律,分配率,那么称这个集合R是一个环
3.线性空间的定义:
设有一个多项式k[x]可以由
集合 s={1,x, x^2,........x^n}重的有限多个多项式线性表示,任意取s中的一个子集s1={x^i.....x^j};
设 k1x^i+............km*x^j=0;
显然k1...km=0,因此s1是线性无关的,从而 s 线性无关 所以s 是 k【x】的一个基。
从而 k【x】是无限维度的线性空间。
4.一元多项式环
设R是一个环,R对加法封闭,R对乘法封闭。
1>若R 的乘法满足交换律,称 R 是交换环
2>若R中有一个元素e,a是一个元
s.t a*e=e*a =a ,则称 e是 单位元,如果还有单位元,单位元只有一个。
3>如果a 属于 R 如果存在 b 属于R 且 b 不为0 使得 a*b=0;
则称a 是一个左零因子或右乘因子。
特别的 0 成为特别0因子
子环的定义:
如果 对于R的加法和乘法运算也成为一个环,则称环R 的一个非空子集合 R1是R的一个子环,
定义 如果 R1中 任意 元 a 属于 R1,且 -a 属于R1则称R 1是R的一个子环。
同构映射的应用:
这里直接简化来理解:
因为(x+3)^2 =(x^2+6*x+9)
设矩阵A ,单位矩阵 I;
显然 有子环定义 矩阵 矩阵 I是矩阵 A 的一个子环。
那么 (A+3*I)^2= A^2+6*A+9*I(把A 看作x ,I看作常数 1);
同构映射,一个双映射中元素是一 一对应的,且对加法运算和乘法运算保持封闭
例如:f(x)+g(x)=h(x),f(x)*g(x)=p(x)
定理1
设K是一个 数域,R 是一个由单位环 I 的交换环,且K到R1 有一个同构映射 t

文章来源地址https://www.toymoban.com/news/detail-443380.html
上图表示的是任意给 t 属于 R ,令k【x】------>R 的映射
设t 是 f【x】的同构映射,由于 f(x)的表示方法唯一。
通用性质: 设 f(x)+g(x)=h(x),f(x)*g(x)=p(x);
则 f(t)+g(t)=h(t),f(t)*g(t)=p(t)用t 带入。文章来源:https://www.toymoban.com/news/detail-443380.html
到了这里,关于高等代数--多项式与线性空间的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!