【无码专区12】子集和（背包dp）-Toy模板网

这篇具有很好参考价值的文章主要介绍了【无码专区12】子集和（背包dp）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

此题已自我实现，但仍归于无码专区

本题在考场上就过了，所以难度并不高，发现性质即可。

problem

有 $n$ 个正整数 $a_1,a_2,...,a_n$ ，他们的和为 $m$ 。你想对于其每一个子集 $S$ ，求出他们的和。

给定 $2^n$ 个 $[0, m]$ 之间的和，其中数字 $i$ 出现了 $b_i$ 次。

求还原 $a$ ，数据保证有唯一解。

$n\le 50,m\le 10000,1s,128MB$

my idea

首先就能知道 $b_0,b_m$ 一定是 $1$ 。

马上就发现最小的 $a_i$ 是没有能被其他数组合出来的情况的，因为他们全是正数！

所以最小的 $b_i\neq 0$ 的 $i$ ，就意味着 $a$ 中原来有 $b_i$ 个 $i$ 。

然后考虑第二小的 $b_j\neq 0$ 的 $j$ ，会注意到有可能 $b_i$ 个 $i$ 可能会组合出 $j$ 。

减去这些组合就是 $a$ 中原本有 $b_j'$ 个 $j$ 。

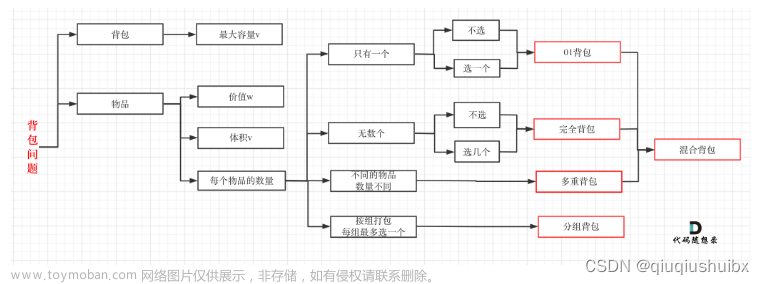
发现这就是个背包 $d p$ 的过程。

容量 $m$ ，但最多只会背包 $n$ 次。

所以跑得很快。

solution

与我的想法相同。

每次找到子集中最小的元素，也就是最小的 $b_i$ 不等于 $0$ 的 $i$ ，然后从背包里删去即可。

删除就是可以理解成逆向执行一下背包中加入元素 $x$ 的操作，也就是从小到大，执行 $b_i-=b_{i-x}$ 。

code文章来源地址https://www.toymoban.com/news/detail-443453.html

#include <bits/stdc++.h>
using namespace std;
#define maxn 55
#define maxm 10005
#define int long long
int n, m, cnt;
int b[maxm], a[maxn], f[maxm];
int c[maxn][maxn];

signed main() {
    freopen( "subset.in", "r", stdin );
    freopen( "subset.out", "w", stdout );
    scanf( "%lld %lld", &n, &m );
    for( int i = 0;i <= n;i ++ ) {
        c[i][0] = c[i][i] = 1;
        for( int j = 1;j < i;j ++ )
            c[i][j] = c[i - 1][j - 1] + c[i - 1][j];
    }
    for( int i = 0;i <= m;i ++ ) scanf( "%lld", &b[i] );
    f[0] = 1;
    for( int i = 1;i <= m;i ++ ) {
        b[i] -= f[i];
        if( ! b[i] ) continue;
        for( int j = 1;j <= b[i];j ++ ) a[++ cnt] = i;
        for( int j = m;j;j -- ) {
            for( int k = 1;k <= b[i];k ++ )
                if( j < k * i ) break;
                else f[j] += f[j - k * i] * c[b[i]][k];
        }
    }
    for( int i = 1;i <= n;i ++ ) printf( "%lld ", a[i] );
    return 0;
}