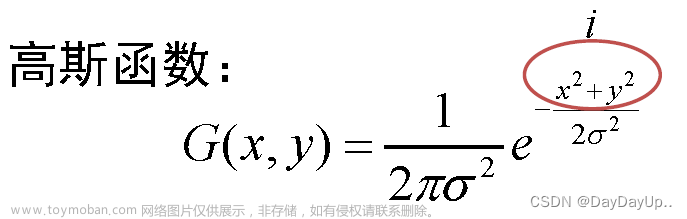【数字图像处理】空间滤波-Toy模板网

这篇具有很好参考价值的文章主要介绍了【数字图像处理】空间滤波。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1. 概述

图像空间滤波是一种常用的图像处理技术，用于改变图像的亮度、对比度、锐度、噪声等特性。它是一种直接在图像空间进行像素操作的处理方法，与频域滤波不同，频域滤波是通过对图像进行傅里叶变换，然后在频域进行滤波处理。本文仅对常用的低通和高通空间滤波进行概括和总结。

2 低通（平滑）滤波

2.1 均值滤波

假设均值滤波器的大小为 $n\times n$ ，则该卷积核可以表示为如下的 $n\times n$ 矩阵：
$\frac{1}{n^2} \begin{pmatrix} 1 & 1 & \cdots & 1 \\ 1 & 1 & \cdots & 1 \\ \vdots & \vdots & \ddots & \vdots \\ 1 & 1 & \cdots & 1 \\ \end{pmatrix}$
其中，矩阵中的每个元素都是 $1/n^2$ ，表示该像素点的权重值等于周围所有像素点的权重之和的平均值。这样，在卷积操作时，该卷积核将对图像中的每个像素点取周围像素点的平均值，从而实现平滑处理。

需要注意的是，均值滤波器的大小 $n$ 越大，滤波器的平滑程度越强，但也可能会导致图像细节的丢失。因此，在实际应用中需要根据具体的需求和图像特点选择合适的滤波器大小。

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取彩色图像
img = cv2.imread('example.jpg')

# 添加高斯噪声
mean = 0
var = 0.5
sigma = var ** 0.5
gaussian = np.random.normal(mean, sigma, img.shape)
noisy_img = np.clip((img/255.0 + gaussian)*255, 0, 255).astype(np.uint8)

# 使用不同大小的卷积核进行均值滤波
k_sizes = [3, 13, 23, 33]  # 卷积核大小
fig, axs = plt.subplots(1, 6, figsize=(12, 3))
axs[0].imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB))
axs[0].set_title("Original")
axs[1].imshow(cv2.cvtColor(noisy_img, cv2.COLOR_BGR2RGB))
axs[1].set_title("Noisy")

for i, ksize in enumerate(k_sizes):
    # 使用均值滤波器进行处理
    denoised_img = cv2.blur(noisy_img, (ksize, ksize))

    # 显示处理后的图像
    axs[i+2].imshow(cv2.cvtColor(denoised_img, cv2.COLOR_BGR2RGB))
    axs[i+2].set_title(f"Denoised (ksize={ksize})")

plt.tight_layout()
plt.show()

【数字图像处理】空间滤波
从实验结果可以看出，均值滤波器的卷积核尺寸越大，去噪强度越高，但同时图像也越模糊。

2.2 中值滤波

中值滤波的原理是将像素点周围的邻域中的像素灰度值排序，然后取中间值作为该像素的灰度值。由于中值滤波是一种非线性滤波方法，其不受噪声分布的影响，可以有效地去除图像中的椒盐噪声和斑点噪声，并且可以保留图像的边缘信息和细节信息。

中值滤波的具体操作步骤如下：

选定滤波器的大小，通常取一个奇数的正整数，如 $\times 3$ 、 $\times 5$ 等。
针对每个像素点，将其周围的邻域像素点的灰度值排序，从小到大排列。
取排序后的中间值作为该像素点的新灰度值。
对于边缘上的像素，可以选择对其不做处理或者根据需要进行特殊处理。

import numpy as np
import matplotlib.pyplot as plt
import cv2
import random

# 添加椒盐噪声
def pepper_and_salt(img, percentage):
    num = int(percentage * img.shape[0] * img.shape[1])  # 椒盐噪声点数量
    img2 = img.copy()
    for _ in range(num):
        X = random.randint(0, img2.shape[0] - 1)
        Y = random.randint(0, img2.shape[1] - 1)
        if random.randint(0, 1) == 0:  # 黑白色概率55开
            img2[X, Y] = (255, 255, 255)
        else:
            img2[X, Y] = (0, 0, 0)
    return img2

# 读取彩色图像
img = cv2.imread('example.jpg')
noisy_img = pepper_and_salt(img, 1.0)

blur_mean = cv2.blur(noisy_img, ksize=(5, 5))
blur_median = cv2.medianBlur(noisy_img, ksize=5)

# 显示原始图像、噪声图像和滤波后的图像
fig, axs = plt.subplots(1, 4)
axs[0].imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB))
axs[0].set_title('Original')
axs[1].imshow(cv2.cvtColor(noisy_img, cv2.COLOR_BGR2RGB))
axs[1].set_title('Noisy')
axs[2].imshow(cv2.cvtColor(blur_mean, cv2.COLOR_BGR2RGB))
axs[2].set_title('Mean Filtered')
axs[3].imshow(cv2.cvtColor(blur_median, cv2.COLOR_BGR2RGB))
axs[3].set_title('Median Filtered')
plt.show()

【数字图像处理】空间滤波
从实验结果可以看出，相比均值滤波，中值滤波能够更有效地去除椒盐噪声。

2.3 高斯低通滤波

通常我们使用的高斯模糊指的是高斯低通滤波，高斯滤波是一种线性平滑滤波方法，常用于图像降噪、模糊和平滑处理。高斯滤波的核心思想是对图像进行加权平均，其中每个像素的权重由高斯分布函数确定。由于高斯分布函数具有平滑性，因此高斯滤波可以在保持图像边缘信息的同时，减小图像的噪声和细节。

高斯滤波的具体操作步骤如下：

选定高斯核大小，通常取一个奇数的正整数，如 $\times 3$ 、 $\times 5$ 等，并计算出高斯分布函数。
对于每个像素点，在其周围的邻域内应用高斯核，并将每个像素点的值与其邻域内像素点的加权平均值进行替换。
对于边缘上的像素，可以选择对其不做处理或者根据需要进行特殊处理。

高斯滤波的公式可以表示为：
$\frac{1}{2\pi\sigma^2}\sum_{i=-\lfloor k/2 \rfloor}^{\lfloor k/2 \rfloor}\sum_{j=-\lfloor k/2 \rfloor}^{\lfloor k/2 \rfloor}I(x+i,y+j) \cdot \exp\left(-\frac{i^2+j^2}{2\sigma^2}\right)$ 其中， $I (x, y)$ 表示原始图像中坐标为 $(x, y)$ 的像素点的灰度值， $I^{'} (x, y)$ 表示滤波后图像中坐标为 $(x, y)$ 的像素点的灰度值， $k$ 表示高斯核的大小， $\sigma$ 表示高斯核的标准差。

2.4 双边滤波

双边滤波的基本原理是将每个像素周围的像素按照它们的像素值和像素间距离进行加权平均。这里的像素间距离是指像素之间的欧几里得距离或者曼哈顿距离等。在加权平均的过程中，距离较近且像素值相似的像素将被赋予更大的权重，距离远或像素值不相似的像素将被赋予较小的权重。
$\begin{aligned} I_{\text{filtered}}(x,y) = \frac{1}{W_p}\sum_{i=-k}^{k}\sum_{j=-k}^{k}w_{ij}(x,y)f(i+x,j+y)\\ w_{ij}(x,y) = \omega_{ij}(x,y)\cdot\phi_{ij}(x,y) \\ \omega_{ij}(x,y) = \text{exp}\left(\frac{-(i^2+j^2)}{2\sigma_d^2}\right) \\ \phi_{ij}(x,y) = \text{exp}\left(\frac{-(f(i+x,j+y)-f(x,y))^2}{2\sigma_r^2}\right) \\ W_p = \sum_{i=-k}^{k}\sum_{j=-k}^{k}\omega_{ij}(x,y)\cdot\phi_{ij}(x,y) \end{aligned}$
其中， $I_{\text{filtered}}(x,y)$ 是双边滤波后的像素值， $f (i + x, j + y)$ 是在位置 $(i + x, j + y)$ 处的原始像素值， $w_{ij}(x,y)$ 是像素 $(i + x, j + y)$ 对像素 $(x, y)$ 的权重， $\omega_{ij}(x,y)$ 是距离权重， $\phi_{ij}(x,y)$ 是像素值相似性权重， $W_p$ 是归一化因子， $k$ 是滤波器的半径， $\sigma_d$ 和 $\sigma_r$ 分别是距离和像素值相似性的标准差。

距离权重 $\omega_{ij}(x,y)$ 用于衡量像素 $(i + x, j + y)$ 与像素 $(x, y)$ 之间的距离，距离越近，权重越大。像素值相似性权重 $\phi_{ij}(x,y)$ 用于衡量像素 $(i + x, j + y)$ 和像素 $(x, y)$ 之间的像素值相似性，像素值越相似，权重越大。最后，归一化因子 $W_p$ 用于将所有像素的权重加起来归一化到 $[0, 1]$ 的范围内，确保滤波后的像素值仍然在原始像素值的范围内。

2.5 导向滤波

导向滤波（guided filter）是一种非线性滤波方法，旨在平滑图像并保留其细节。导向滤波是双边滤波的一种扩展，它使用一张辅助图像作为滤波器的导向信息，这张图像应当与待处理的原始图像在一定程度上相关。导向滤波器的输出是输入图像的加权平均值，其中权重由导向图像和滤波器参数决定。

以下是导向滤波的数学公式：

设 $I$ 是待处理的原始图像， $p$ 是该图像中的像素点， $I_p$ 表示该像素的亮度值。设 $p^{'}$ 是导向图像中的像素点， $P_{p'}$ 表示该像素的亮度值。那么在导向滤波中，滤波器的输出 $q_p$ 可以表示为：
$q_p=\frac{1}{\omega_p}\sum_{p'\in\mathcal{N}_p}f(I_{p'}, P_{p'})I_{p'}$ 其中， $\mathcal{N}_p$ 表示像素点 $p$ 周围的邻域， $\omega_p$ 是归一化的权重系数，可以表示为：
$\omega_p=\sum_{p'\in\mathcal{N}_p}f(I_{p'}, P_{p'})$ 函数 $f$ 可以使用以下的高斯函数：
$f(I_{p'}, P_{p'})=\frac{1}{\sqrt{2\pi}\sigma_s}\text{exp}\left(-\frac{\lVert p-p'\rVert^2}{2\sigma_s^2}\right)\cdot\frac{1}{\sqrt{2\pi}\sigma_r}\text{exp}\left(-\frac{\lVert I_p-I_{p'}\rVert^2}{2\sigma_r^2}\right)$ 其中， $\mathcal{N}_p$ 表示像素点 $p$ 周围的邻域， $\sigma_s$ 和 $\sigma_r$ 是两个参数，分别控制空间距离和亮度差异对滤波结果的影响。

可以看出，导向滤波的核心思想是使用辅助图像来调整卷积核的权重，从而在滤波过程中保留图像的结构信息和纹理信息，同时抑制噪声。

辅助图像通常可以是：原始图像、模糊图像、边缘图像、梯度图像或者是以上图像的自适应组合。

3 高通（锐化）滤波

3.1 Laplacian滤波器

拉普拉斯滤波器是一种常用的图像处理滤波器，它可以增强图像中的边缘特征，同时抑制图像中的高频噪声。其数学原理基于拉普拉斯算子，其作用类似于对图像进行二阶微分，从而提取出图像中的高频信息。

具体来说，拉普拉斯滤波器对于图像中的每个像素，会将其周围像素与自身像素的加权和减去自身像素的权重，从而得到该像素的滤波结果。这个权重矩阵通常是一个3x3或5x5的矩阵，例如：
$\begin{bmatrix}0 & 1 & 0 \\ 1 & -4 & 1\\ 0 & 1 & 0\end{bmatrix}$ 这是一个3x3的拉普拉斯核，其中中心像素的权重是-4，周围像素的权重为1。这个核可以用于对图像进行边缘检测，因为它会强调图像中的高频分量，即图像中的边缘。

另外，拉普拉斯滤波器还可以通过对原始图像和滤波后的图像求差来实现图像锐化。这是因为拉普拉斯滤波器可以增强图像中的高频分量，从而使图像的细节更加明显。

3.3 Sobel滤波器

Sobel滤波器采用两个3×3的卷积核，一个用于检测水平边缘，另一个用于检测垂直边缘。

卷积核如下所示：
$G_{x} = \begin{bmatrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{bmatrix},\ G_{y} = \begin{bmatrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1 \end{bmatrix}$