【算法】减治法详解-Toy模板网

这篇具有很好参考价值的文章主要介绍了【算法】减治法详解。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、减治法概述

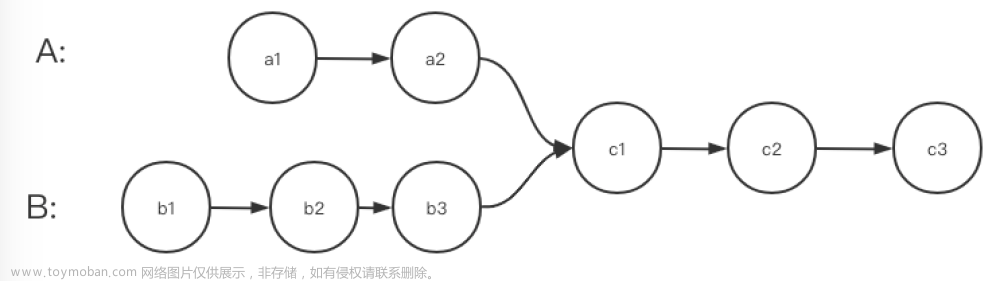
分治法是将一个大问题划分为若干个子问题，分别求解后将子问题的解进行合并得到原问题的解。减治法同样是讲一个大问题划分为若干个小的子问题，但是这些子问题不需要分别求解，只需要求解其中一个子问题便可，因此也不需要对子问题进行合并，可以说，减治法是一种退化版的分治法。

设计思想
减治法将原问题分解为若干个子问题，并且原问题的解和子问题的解之间存在某种确定的关系。一般存在两种情况：

原问题的答案存在于其中一个子问题中
原问题的答案和子问题的答案存在某种联系

简单事例：两个序列的中位数
问题描述：
一个长度为n的升序序列S中位于其n/2处的元素称之为S的中位数。现在有两个等长的升序序列A和B，求这两个序列的中位数。

基本思想：

分别求出两个序列的中位数，记作a和b
比较a和b，有下列三种情况：
- a=b，则a就是两个序列的中位数
- a<b，证明中位数只能出现在a和b之间，序列S1抛弃a之前的元素，序列S2抛弃b之后的元素
- a>b，证明中位数只能出现在b和a之间，序列S2抛弃b之前的元素，序列S1抛弃a之后的元素
重复上述过程，直到两个序列中只有一个元素，则较小者就是所求元素。

算法分析
由于每次求完两个序列的中位数后，得到的两个子序列大多是原来长度的一半，因此循环执行nlog₂n次，时间复杂度为O(nlog₂n)。空间复杂度为O(1）

二、查找问题中的分治法

2.1 折半查找

折半查找又称为二分查找，只适用于有序的顺序表。其特点是将顺序表划分为一颗区间二叉树。该算法只适用于顺序存储结构，不适用于链式存储结构，并且要求元素关键字有序排列。

折半查找李永乐序列有序的特变，首先取序列中间记录作为比较对象，那如果给定值和中间值相等则查找成功；如果给定值小于中间记录，则在中间记录的左半区继续查找；如果给定值大于中间记录，则在中间记录的右半区继续查找。重复上述步骤知道查找成功。

平均时间复杂度为O(log₂n)。但是折半查找的速度不一定比顺序查找快

查找判定树
二分查找的过程可以构造出一个查找判定树
【算法】减治法详解
当low和high之间有奇数个元素，则mid分割后，左右两部分元素相等；
当low和high之间有偶数个元素，则mid分割后，左半部分比右半部分少一个元素

因此，在判定树中，如果 $mid=\lfloor(low+high)/2\rfloor$ ，则右子树结点数-左子树结点数=0或者1；，如果 $mid=\lceil(low+high)/2\rceil$ ，则左子树结点数-右子树结点数=0或者1

折半查找判定树一定是平衡二叉树，并且只有最下面一层是不满的，因此元素个数为n的时候树高为 $\lceil log_2(n+1)\rceil$ 。n个元素的判定树的失败节点有n+1个

折半查找每和待查找值比较一次，剩下的待查找元素就减少一半，将原问题不断缩减成规模更小的问题，并且不需要进行合并，因此折半查找属于减治法的成功应用。

2.2 二叉查找树

定义

左子树上的结点都小于根节点、所有右子树都大于根节点
使用中序遍历可以得到一个递增的有序序列

查找具体值的代码实现

从根节点开始，如果小于根节点则往左走，大于根节点则往右走，其路径是不会出现分叉的，也就是说，对BST的查找是不会出现回溯的

// 查找二叉排序树具体结点
BiTree *BST_Search(BiTree t, int v){
    while (t!=NULL){
        if (t.data>v){
            t=t.rchild;
        }else if (t.data < v){
            t = t.rchild;
        }else{
            return t;
        }
    }
    return t;
}

// 查找二叉排序树具体结点（递归）
BiTree *BST_Search1(BiTree t, int v){
    if (t==NULL || t.data==v){
        return t;
    }
    if (t.data < v){
        BST_Search1(t.rchild,v);
    }else{
        BST_Search1(t.lchild, v);
    }
}

非递归的空间复杂度为O(1)，递归的空间复杂度为O(n)
在BST的查找中，如果生成的BST平衡，那么其最大查找次数最小，为 $log_2n +1$ ;如果生成的BST及其不平衡，比如生成BST时的元素插入顺序恰好是递增或递减，那么最大查找次数最大，为n

插入

如果二叉树为空，则直接插入，否则，如果关键字k小于根节点，则插入左子树，如果关键字大于根节点，则插入右节点。新插入的结点一定是叶子结点。采用递归调用的方法空间复杂度为O(H)，H为树高；采用非递归的空间复杂度为O(1)

// 二叉排序树的插入(递归)
int BST_insert(BiTree &t, int v){
    if (t==NULL){   //已经到了根节点
        t = (BiTree)malloc(sizeof (BiTree));
        t.data=v;
        t.lchild=t.rchild=NULL;
        return 1;
    }else if (k<t.data){
        BST_insert(t.lchild,v);
    }else if (k>t.data)
        t = BST_insert(t.rchild,v);
    else
        return 0
}

删除

叶子结点直接删除
删除的结点n只有左子树，那么让其子树的根节点替代他的位置，成为n的父节点的子树
同样，删除的结点n只有右子树，那么让其子树的根节点替代他的位置，成为n的父节点的子树
删除的结点n既有左子树又有右子树。那么：
- 可以中序遍历右子树，其第一个节点p为右子树中最小的结点（也就是右子树中最左下的结点），让结点p替代结点n的位置
- 可以遍历左子树，取得左子树中最小的结点p（也就是左子树中最右下的结点），让结点p替代结点n的位置

效率分析

查找长度：在查找运算中，需要对比关键字的次数反映了查找操作时间的复杂度。平均查找长度又称为ASL。需要会算二叉排序树的平均查找长度。查找失败所需要的平均长度也要会计算，一般只有查找到叶子结点仍未查找到目标值，则判定为查找失败

二叉排序树的ASL的优劣很大情况下取决于树的高度，因此树的高度越小，性能越优秀。而构造二叉树的输入序列有序会导致一个倾斜的单支树，此时BST高度最高，性能最差。如果构造出来的是一颗平衡二叉树，则性能最好。其最好查找长度为O(logn)，最坏查找长度为O(n)。

三、排序问题中的减治法

3.1 插入排序

3.2 堆排序

四、组合问题中的减治法

4.1 淘汰赛冠军问题

问题：
假设有n=2^k个选手在进行竞技淘汰赛，要选出最后的冠军，请设计淘汰赛的过程。

想法：
竞技淘汰赛最自然的赛制是一个队伍两个选手pk，胜利者和另外一队的胜利者pk，再次决出胜利者，进入下一轮的淘汰。这样的赛制会类似于一颗二叉树，两个孩子节点pk选出胜者成为他们的父节点。下面开始考虑减治法，首先将选手两两分为n/2组，进行了一轮淘汰后，还剩下n/4组，以此类推直到还剩最后一个选手则为冠军

4.2 假币问题

问题：
在一堆硬币中有一个假币，假币的重量比较轻，然后可以使用一个天平去对比两组硬币孰轻孰重，假币问题就是要设计一个高效的算法来选出这一枚硬币。

算法思想：
解决假币问题最自然的想法一分为二，将n枚硬币一分为二分为均等的两组，如果n为奇数则留下一枚硬币，保证两组数量均等。如果两组硬币重量相同，那么留下的硬币则是假币，如果左边的天平更轻，证明假币在左边的硬币组中，反之在右边的硬币组中。对较轻的组同样采用上述的处理方法，直到找到假币为止。在假币问题中，每次我们都将硬币分为两组，每次使用天平后都会使得问题规模减小一半，因此这是一个减治法问题。根据上述描述，可以知道时间开销为O(log₂n)

但是这都不是最优解法，其实可以将硬币等分为3组，如果不整除则余下的硬币加在第三组中。将第一组和第二组放上天平，如果一组和二组重量相等，那么假币肯定在第三组，因此可以对第三组执行上述操作，反之则在第一组或者第二组中。这种方法每次可以将问题规模减小至原来的1/3，因此其时间开销为O(log₃n)文章来源地址https://www.toymoban.com/news/detail-444237.html

到了这里，关于【算法】减治法详解的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！