| 一、实验目标: 熟悉和掌握A*算法实现迷宫寻路功能,要求掌握启发式函数的编写以及各类启发式函数效果的比较。 |
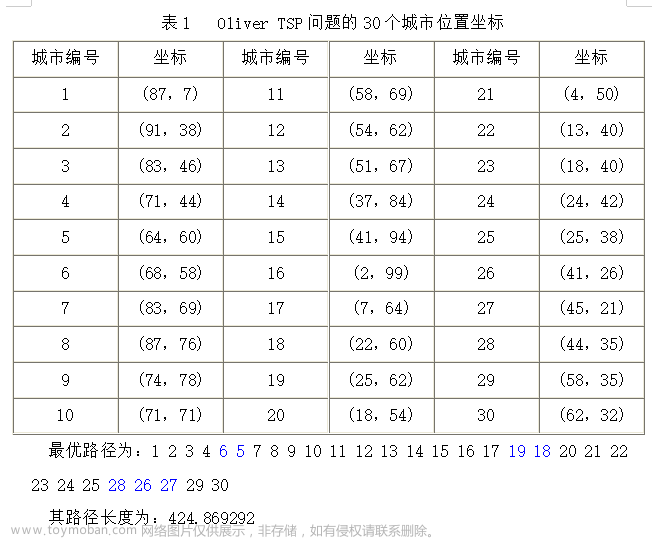
| 二、实验内容与完成情况: 寻路问题常见于各类游戏中角色寻路、三维虚拟场景中运动目标的路径规划、机器人寻路等多个应用领域。迷宫寻路问题是在以方格表示的地图场景中,对于给定的起点、终点和障碍物(墙),如何找到一条从起点开始避开障碍物到达终点的最短路径。 假设在一个n×m 的迷宫里,入口坐标和出口坐标分别为(1,1)和(5,5) ,每一个坐标点有两种可能:0或1,其中0表示该位置允许通过,1表示该位置不允许通过。 如地图: 0 0 0 0 0 1 0 1 0 1 0 0 1 1 1 0 1 0 0 0 0 0 0 1 0 最短路径应该是: A B 0 0 0 1 C 1 0 1 E D 1 1 1 F 1 J K L G H I 1 M 即:(1,1)-(1,2)-(2,2) -(3,2)-(3,1)-(4,1)-(5,1)-(5,2)-(5,3)-(4,3)-(4,4)-(4,5) -(5,5) 以寻路问题为例实现A昇法的水解程序(编程语言不限),要求设计两种不同的估价函数。 实验要求: 1.画出用A”算法求解迷宫最短路径的流程图。 2.设置不同的地图,以及不同的初始状态和目标状态,记录A`算法的求解结果,包括最短路径、扩展节点数、生成节点数和算法运行时间。 3.对于相同的初始状态和目标状态,设计不同的启发式函数,比较不同启发式函数对迷宫寻路速度的提升效果,包括扩展节点数、生成节点数和算法运行时间。 |
| 三、实验步骤与结果: 首先在5×5的地图上实现A*算法: 1、根据A*算法的特点:f(n) = g(n) + h(n),需要设计两个函数来满足A*算法。 g(n)为起点到当前点的距离 h(n)是对当前方格到目的地方格距离的估算,估算方法设计两种:
2、定义一个地图
3、创建Openlist和Closelist,由于在本实验中,设定的移动方向只有上、下、左、右,所以第一步从起始点开始判断。 将起始点放入Openlist和Closelist中,从起始点开始判断其周围可以到达的方格点,将当前点从Openlist中移除,找到周围f最小的方格点。
将其放入Openlist中,然后将当前点放入Closelist中,Closelist中的方格点不可再访问,所以需要在更新函数上增加对周围方格点是否在Closelist的判断。 当移动到f最小的点后,重复上述操作。 4、 5×5实验结果如下: 采用欧几里得距离时:
采用曼哈顿距离时:
通过实验结果我们可以看到,在地图为5×5大小时,扩展节点数,生成节点数和算法时间没有明显的差距。 5、下面通过20×20的地图进行比较: 曼哈顿距离函数:
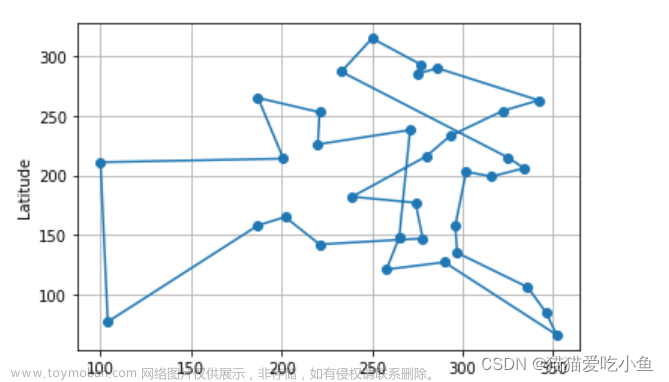
点的移动轨迹为: [1,1]-->[2,1]-->[3,1]-->[4,1]-->[4,2]-->[4,3]-->[3,3]-->[3,4]-->[3,5]-->[4,5]-->[5,5]-->[6,5]-->[7,5]-->[8,5]-->[9,5]-->[9,6]-->[9,7]-->[9,8]-->[9,9]-->[9,10]-->[9,11]-->[10,11]-->[10,12]-->[10,13]-->[9,13]-->[9,14]-->[9,15]-->[10,15]-->[11,15]-->[12,15]-->[13,15]-->[13,14]-->[12,14]-->[12,13]-->[12,12]-->[12,11]-->[12,10]-->[12,9]-->[12,8]-->[12,7]-->[13,7]-->[14,7]-->[15,7]-->[16,7]-->[16,6]-->[16,5]-->[16,4]-->[17,4]-->[18,4]-->[19,4]-->[19,5]-->[19,6]-->[19,7]-->[20,7]-->[20,8]-->[19,8]-->[19,9]-->[18,9]-->[18,10]-->[18,11]-->[19,11]-->[19,12]-->[18,12]-->[18,13]-->[18,14]-->[19,14]-->[20,14]-->[20,15]-->[19,15]-->[19,16]-->[19,17]-->[18,17]-->[18,18]-->[18,19]-->[18,20]-->[19,20]-->[20,20] 欧几里得函数:
点的移动轨迹为: [1,1]-->[2,1]-->[3,1]-->[4,1]-->[4,2]-->[4,3]-->[3,3]-->[3,4]-->[3,5]-->[4,5]-->[5,5]-->[6,5]-->[6,6]-->[7,6]-->[7,7]-->[8,7]-->[8,8]-->[9,8]-->[9,9]-->[9,10]-->[9,11]-->[10,11]-->[10,12]-->[10,13]-->[9,13]-->[9,14]-->[9,15]-->[10,15]-->[11,15]-->[12,15]-->[13,15]-->[13,14]-->[12,14]-->[12,13]-->[12,12]-->[12,11]-->[12,10]-->[12,9]-->[12,8]-->[12,7]-->[13,7]-->[14,7]-->[15,7]-->[16,7]-->[16,6]-->[16,5]-->[16,4]-->[17,4]-->[18,4]-->[19,4]-->[19,5]-->[19,6]-->[19,7]-->[19,8]-->[19,9]-->[18,9]-->[18,10]-->[18,11]-->[18,12]-->[18,13]-->[18,14]-->[18,15]-->[18,16]-->[18,17]-->[18,18]-->[18,19]-->[18,20]-->[19,20]-->[20,20]文章来源:https://www.toymoban.com/news/detail-444443.html 通过比较我们可以得到,欧几里得距离函数相对于曼哈顿函数来说,扩展的节点数以及生成的节点数都要更少,算法的运行时间也要比曼哈顿距离算法的时间要更短一些,总体来说欧几里得距离算法比曼哈顿距离算法的性能要更好。文章来源地址https://www.toymoban.com/news/detail-444443.html |
到了这里,关于A*算法求解迷宫寻路问题实验的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!