占个位置吧,开始在本帖实时更新2023长三角高校数学建模赛题思路代码,文章末尾获取!
持续为更新参考思路
赛题思路
A题思路:
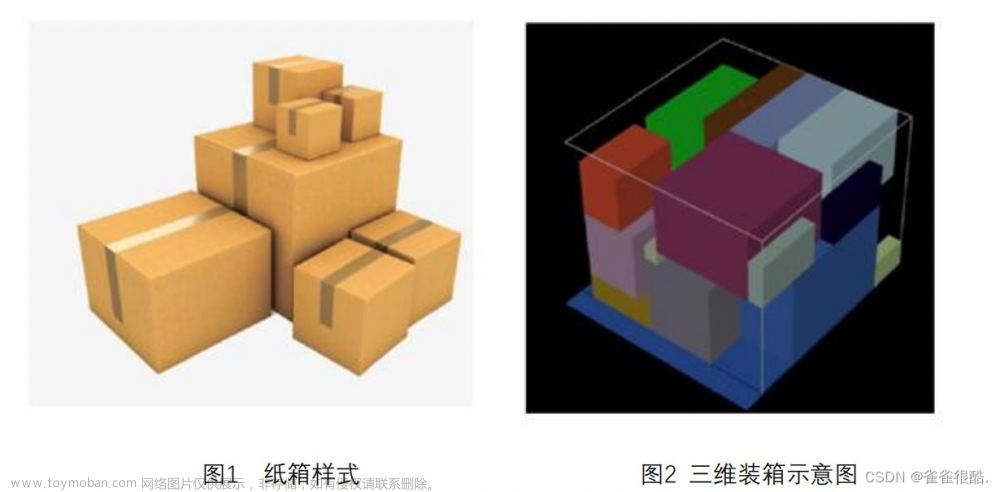
该题是一个物流和供应链管理的优化类问题,考虑使用贪心算法、模拟退火、遗传算法来找到最优解。这个题目说实话有点难度的,三维切割问题,不太建议新手同学去选择。
问题1.针对附件1装箱数据中给出的订单数据和耗材数据,对每个订单,分 别用箱子或袋子去装,请设计出合适的装载方案,要求使用耗材数量越少越好, 在耗材数量相同时,耗材总体积越小越好。给出每种耗材的使用总数和耗材总体积。
问题一是一个经典的装箱问题,又叫作背包问题,需要我们寻找最优装载方案,即使用最少的耗材(箱子或袋子)来装载所有物品。这个问题主要涉及到两个核心点:① 对于每个订单,我们需要选择合适的包装方式(箱装、袋装或混合装),以便最大程度地减少耗材数量;②在耗材数量相同的情况下,我们需要选择体积更小的耗材,以降低运输成本。
对于这个问题,我们可以采取像贪婪算法,最佳适应算法,最坏适应算法等。来寻找到近似的最优解,而且它们的计算效率较高。另外,我们还需要对各种包装方式进行混合使用,以寻找最优解。比如对于一些体积较小、数量较多的物品,我们可能会优先考虑使用袋子进行打包,因为袋子的可变形特性使得其在装载小物品时能够节省更多空间。
问题2.针对附件1的数据,现在需要优化耗材的尺寸,请给出耗材尺寸的优 化方案。要求优化后耗材的种数不变,只是改变耗材尺寸;对问题1中成功装载 的物品,优化后的方案使用的箱子或袋子数尽量减少;总体积不能超过原方案的 总体积;在耗材数量相同时,耗材总体积越小越好。给出优化后的每种耗材的具 体尺寸、使用总数和耗材总体积。
问题二是关于优化耗材尺寸的问题。这个问题的核心是在保持耗材种数不变的前提下,通过优化耗材尺寸,使得对问题一中成功装载的物品,优化后的方案使用的箱子或袋子数尽量减少,同时总体积不能超过原方案的总体积。
对于这个问题,我们首先需要进行详细的数据分析,以便找出最频繁使用的耗材尺寸,以及它们所对应的物品类型和数量。然后,我们可以根据这些信息来优化耗材的尺寸。比如如果我们发现大部分的物品都能装入一种特定大小的箱子/袋子,那么我们可以考虑增大这种尺寸的耗材的生产量,从而减少其他尺寸耗材的使用。还需要考虑到物品的形状和大小的多样性,以保证新的耗材尺寸能够适应大多数的物品。
问题3.以上两个问题假设货物与耗材都为刚性的,若货物与耗材存在柔性 或者可轻微挤压的属性时,请重新完成问题 1、2。根据实际情况,这里考虑耗 材伸展时,长、宽、高都不超过原尺寸的 5%。
问题三引入了新的变量:货物与耗材的柔性。这道题就稍微有些难度了,因为我们需要考虑货物和耗材在被挤压或伸展时的行为。比如某些货物可能在被挤压时会发生形状的变化,这会影响它们的装载方式和装载效率。同样,柔性的耗材可能在装载过程中发生形状的变化,这也会影响装载效率。
在解决这个问题时,我们需要引入一些新的假设和约束,例如货物和耗材的弹性、耗材的最大伸展量等。这意味着我们需要对物品和耗材的物理特性有深入的了解,以便更准确地模拟它们在装载过程中的行为。
这里我们就需要修改我们的优化算法,来适应这些新的约束。我们需要考虑物品和耗材的弹性在装载过程中的影响,可以使用例如遗传算法或模拟退火算法,来寻找最优解。
B题思路:
这个题目是一个典型大数据题目。需要预测新能源汽车市场的未来发展,以及分析新能源汽车发展与碳排放目标的关系。难度系数不算很高。主要在于收集和处理数据。
问题 1. 对长三角地区新能源汽车的发展情况进行分析,研究长三角地区新 能源汽车生产在全国新能源汽车市场的地位及作用,预测未来 3 年长三角地区新能源汽车的市场保有量。
在分析长三角地区新能源汽车的发展情况时,首先需要收集关于新能源汽车生产和销售的相关数据,包括但不限于生产量、销售量、市场份额、生产企业数量等。这些数据可以从官方统计数据、汽车产业报告、新闻报道等渠道获取。
分析这些数据时,我们需要考虑一些可能影响新能源汽车发展的因素,如政策支持、市场需求、充电设施的建设等。这些因素可能会对新能源汽车的生产和销售产生重大影响。我们可以使用统计分析或者机器学习的方法,如回归分析、时间序列分析等,来建立长三角地区新能源汽车市场保有量的预测模型。
问题 2. 新能源汽车行业的快速发展,给传统燃油汽车带来了极大的挑战, 请研究我国新能源汽车与传统燃油汽车的市场竞争关系,分析该竞争关系受到哪 些因素的影响,给出我国新能源汽车和传统燃油汽车市场保有量随时间变化的演化规律。
新能源汽车与传统燃油汽车的市场竞争关系是一个复杂的问题,涉及到许多因素,如价格、性能、燃料成本、环保政策等。我们需要收集这些因素的数据,然后使用一些量化方法(如对比分析、回归分析等)来研究它们对新能源汽车和传统燃油汽车市场保有量的影响。
具体地,我们可以建立一个竞争模型,如拓扑竞争模型,来描述新能源汽车和传统燃油汽车的竞争关系。在这个模型中,新能源汽车和传统燃油汽车的市场份额可以被看作是竞争的结果,而价格、性能等因素可以被看作是竞争的条件。然后,我们可以用这个模型来预测新能源汽车和传统燃油汽车市场保有量的未来变化。
问题 3. 新能源汽车的发展对双碳目标的实现具有积极推动作用,请研究新 能源汽车发展与双碳的关系,并对长三角地区碳达峰和碳中和的时间进行预测, 如有必要可结合其它相关因素。
新能源汽车的发展对双碳目标的实现具有积极推动作用,因为新能源汽车的使用可以显著减少碳排放。因此,我们需要研究新能源汽车的发展与碳排放的关系。
我们需要收集新能源汽车的碳排放数据,这些数据可以从新能源汽车的生产和使用过程中获取。然后使用这些数据来建立一个模型,描述新能源汽车的发展与碳排放的关系。这个模型可以帮助我们预测新能源汽车发展对碳达峰和碳中和的影响。
还需要去考虑其他可能影响碳排放的因素,比如工业生产、能源消费等。这些因素也需要纳入我们的分析模型中。
对于长三角地区碳达峰和碳中和的时间的预测,我们需要建立一个预测模型,将新能源汽车的发展和其他可能影响碳排放的因素作为输入,碳排放量作为输出。这个模型可以是像时间序列预测模型、、神经网络、深度学习预测模型等。通过训练这个模型,我们可以预测长三角地区碳达峰和碳中和的时间。
这个题目的难点在于新能源汽车的发展和碳排放的关系可能会受到许多因素的影响,我们要去收集尽可能多的相关数据,来提高预测模型的准确性。最后,我们还需要对预测结果进行灵敏度分析,以理解各个输入因素对预测结果的影响。
C题思路:
C题也是一个数据分析类题目,需要找到合适的数据源,并且能够有效地清洗和处理数据。难度不高,优先可以考虑。
问题1. 量化分析 2023 年考研有多难,导致考研难的主要因素有哪些?
这个问题主要考察的是能否从数据中提取出影响考研难度的主要因素,并且量化这种难度。我们先要去收集相关的数据,包括像每年的报考人数、录取人数、录取学校的信息、专业信息、保研人数包括新冠疫情影响等等。数据可以从教育部门的公开数据、学校的公开数据,或者第三方的教育数据提供商那里查得到,后面我会帮大家去搜集数据。
在模型的选择上,我们可以使用主成分分析或者因子分析的方法,从多个指标中提取出主要的影响因子。考虑使用多元线性回归模型,将考研难度作为因变量,其余的因素像报考人数、录取人数、保研人数等作为自变量,通过模型的拟合,我们可以得到各个因素对考研难度的影响程度。
在量化考研难度的指标上,我们可以选择录取率(录取人数/报考人数)或者竞争比(报考人数/录取人数)作为主要的指标。我们也可以考虑将保研率(保研人数/报考人数)作为影响考研难度的一个因素。
问题2:这个问题要求研究考研难度的历史变化趋势,以及找出近三年考研难度最大的10所学校和10个专业。首先,我们需要收集历史考研数据,包括但不限于报考人数、录取人数、保研人数、保研率等。其次,我们需要使用时间序列分析或其他方法,分析考研难度的变化趋势。然后,我们需要使用适当的指标,比如录取竞争比,找出近三年考研难度最大的学校和专业。
这个问题主要考察的是能否分析出考研难度的历史变化趋势,以及找出近三年考研难度最大的10所学校和10个专业。还是要先去收集相关的数据,这些数据除了包括问题1中的数据,还需要包括历史的考研数据。
这里我们可以使用时间序列分析的方法,比如ARIMA模型,来分析考研难度的历史变化趋势。为了去找出难度最大的10所学校和10个专业,我们可以使用聚类分析的方法,将学校或者专业根据考研难度进行分类,
在指标的选择上,我们还是可以选择录取率或者竞争比作为主要的指标。我们还可以考虑使用录取分数线、平均分数线等作为衡量考研难度的一个指标。
问题 3. 预测未来 3 年考研难度的变化,基于你们的研究给报考 2024 年研究 生的广大考生提几条建议。
这个问题主要考察的是能否预测未来三年的考研难度,并给出相应的建议。在数据收集上,除了问题1和问题2中的数据,我们还需要收集一些可能影响未来考研难度的因素,比如政策变化、招生计划变化等。
当然考研难度委任为肯定还是会逐年增大的哈
包括像:高校招生规模逐年扩大,竞争加剧。
就业市场不景气,考研人数持续增长。
教育部加大对考研的支持力度,考研机会增加。
在这些因素的影响下,考研难度还会呈现出持续上升的趋势。
在模型选择上,我们可以继续使用ARIMA模型来预测未来三年的考研难度。另外,我们也可以考虑使用机器学习的方法,比如支持向量机(SVM)、随机森林等,训练一个预测模型。在模型的训练过程中,我们要将历史的考研数据作为训练集,将未来的考研数据作为测试集。
在给出建议的过程中,我们结合预测的结果和历史的数据分析,给出针对性的建议。比如,如果预测的结果显示未来的考研难度将会增大,那么我们可以建议考生提前准备,尽早确定目标学校和专业,增强自身的竞争力。如果预测的结果显示某些学校或者专业的考研难度将会增大,那么我们可以建议考生对这些学校或者专业有所警惕,合理安排自己的考研计划等等,这些大家就可以去自己分析。文章来源:https://www.toymoban.com/news/detail-444959.html
↓↓↓文章来源地址https://www.toymoban.com/news/detail-444959.html
到了这里,关于2023长三角数学建模竞赛ABC题思路分析的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!