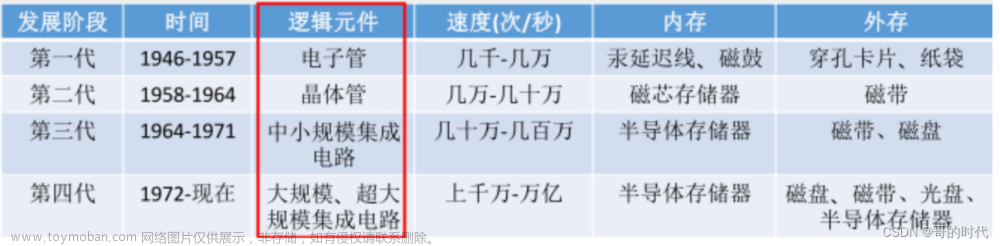
(一)课内习题
1.


















(二)课后练习
1.写出下列各整数的原码、反码和补码表示(用8位二进制表示)。其中MSB是最高位(符号位),LSB是最低位。
(1)-35 (2) -128 (3)-127 (4)-1
答:(1)-35 原: 1011 0101 反:1100 1010 补码:1100 1011
(2) -128 在八位二进制下,-128不能用原码或反码表示,反码只能表示0到127,-0到-127; 补码:1000 0000
(3)-127 原: 1111 1111 反:1000 0000 补码:1000 0001
(4)-1 原: 1000 0001 反:1111 1110 补码:1111 1111
2.设[X]补=a7.a6 a5··· a0 ,其中ai 取0或1, 若要X>-0.5,求a0 a1 a2 ··· a7 的取值。
答:
若a7 =0,则X为正数,显然a0··· a6取任何值均可。
若a7 =1,则X为负数,[X]移=0. a6 a5 ··· a0 ∵ -0.5D = -0.100000B,则[-0.5D ]移=0.100000
∴ 若要X>-0.5,即等价于[X]移> [-0.5D ]移 即0. a6 a5··· a0>0.100000,因此必须是a5··· a0不全为0。
结论: 如果a7 =0, a6··· a0取任何值均可; 如果a7 =1 ,必须满足a6 =1 且a5··· a0不全为0。
3.有一个字长为32位的浮点数,符号位1位,阶码8位,用移码表示,尾数23位,用补码表示,基数为2,请写出:
(1)最大数的二进制表示 (2)最小数的二进制表示 (3)规格化数所能表示的数的范围。
答:
(1)0111 1111 1111 1111 1111 1111 1111 1111
(2)1111 1111 1110 0000 0000 0000 0000 0000
(3)1111111111 0111111111111111111111~0111111111 1000000000000000000000
4. 将下列十进制数表示成浮点规格化数,阶码3位,用补码表示;尾数9位,用补码表示。
(1) 27/64
(2) -27/64
答:

5.已知X和Y, 用变形补码计算X+Y, 同时指出运算结果是否溢出。
(1)X= 11011 Y= 00011
(2)X= 11011 Y= - 10101
(3)X=- 10110 Y=- 00001
答:
(1)先写出x和y的变形补码再计算它们的和
[x]补= 0011011 [y]补=0000011
[x+y]补=[x]补+[y]补=0011011+0000011=0011110
∴ x+y= 11110B 无溢出。
(2)先写出x和y的变形补码再计算它们的和
[x]补= 0011011 [y]补=1101011
[x+y]补=[x]补+[y]补=0011011+1101011= 0000110
∴ x+y= 0110B 无溢出。
(3)先写出x和y的变形补码再计算它们的和
[x]补=1101010 [y]补=1111111
[x+y]补=[x]补+[y]补=1101010+1111111=1101001
∴ x+y= - 10111B,无溢出。
6. 已知X和Y, 用变形补码计算X-Y, 同时指出运算结果是否溢出。
(1) X= 11011 Y= - 11111
(2) X= 10111 Y= 11011
(3) X= 11011 Y=- 10011
答:
(1)先写出x和y的变形补码,再计算它们的差
[x]补=0011011 [y]补=1100001 [-y]补=0011111
[x-y]补=[x]补+[-y]补=0011011+0011111=0111010
∵运算结果双符号不相等 ∴ 为正溢出
X-Y=+11010B
(2)先写出x和y的变形补码,再计算它们的差
[x]补=0010111 [y]补=0011011 [-y]补=1100101
[x-y]补=0010111+1100101=1111100
∴ x-y= -00100B 无溢出
(3)先写出x和y的变形补码,再计算它们的差
[x]补=0011011 [y]补=1101101 [-y]补=0010011
[x-y]补=[x]补+[-y]补=0011011+0010011=0101110
∵运算结果双符号不相等 ∴ 为正溢出
X-Y=+10111B
7. 用原码阵列乘法器、补码阵列乘法器分别计算X×Y。
(1)X= 11011 Y= -11111
(2)X=- 11111 Y=- 11011
答:

8.

9.

10.
解:
11.某加法器进位链小组信号为C4C3C2C1,低位来的进位信号为C0,请分别按下述两种方式写出C4C3C2C1逻辑表达式。
(1)串行进位方式 (2)并行进位方式
12.用IEEE32位浮点格式表示如下的数:
(1)-5 (2)-1.5 (3)384 (4)1/16 (5)-1/32
答:对于所有的数,我们可以将它们表示为以下的形式:(-1)^S × (1.M )× 2^(E-127) 其中S是符号位,M是尾数部分23位,也称为小数部分或分数部分),E是指数部分。注意:我们不直接存储前面的“1.”,而是隐式地将它包含在内。这被称为隐藏的位——相当于节省一个位的存储。
答案:
(1)-5:11000000101000000000000000000000
(2)-1.5: 10111111110000000000000000000000
(3)384:01000011110000000000000000000000
(4)1/16:00111101100000000000000000000000
(5)-1/32 :10111101000000000000000000000000
示例:
-1/32 先转化成小数 -0.03125
- S = 1 (因为数字是负数)
- 把-0.03125写成二进制形式: -0.00001
- 转换为规范化的形式: 1.0×2−51.0×2−5
- E = -5 + 127 = 122 = 01111010 (二进制形式)
- M = 0 (后面用0填充)
结果:10111101000000000000000000000000
13.下列各数使用了IEEE32位浮点格式,相等的十进制是什么?
(1)1 10000011 110 0000 0000 0000 00000000
(2)0 01111110 101 0000 0000 0000 00000000
答案:
(1) 1 10000011 110 0000 0000 0000 00000000
由上题可知,S = 1 (意味着数是负的) E = 10000011 (二进制) = 131 (十进制) M = 110 0000 0000 0000 00000000 = 0.75
所以,该数值为: (−1)1×(1.75)×2(131−127)(−1)1×(1.75)×2(131−127) = -1.75 * 2^4 = -28
(2) 0 01111110 101 0000 0000 0000 00000000
S = 0 (意味着数是正的) E = 01111110 (二进制) = 126 (十进制) M = 101 0000 0000 0000 00000000 = 0.625
所以,该数值为: (−1)0×(1.625)×2(126−127)(−1)0×(1.625)×2(126−127) = 1.625 * 2^-1 = 0.8125文章来源:https://www.toymoban.com/news/detail-445347.html
因此,给定的两个IEEE 32位浮点数对应的十进制数分别为-28和0.8125。文章来源地址https://www.toymoban.com/news/detail-445347.html
14.32位格式最多能表示2^32个不同的数。用IEEE32位浮点格式最多能表示多少不同的数?为什么?

15.设计一个带有原码阵列乘法器(使用芯片)和原码阵列除法器(使用芯片)的定点运算器。
16.设计一个ALU(4位),完成加、减、取反、取补、逻辑乘、逻辑加、传送、加1等8种运算功能。
到了这里,关于计算机组成原理---第二章 习题详解版的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!