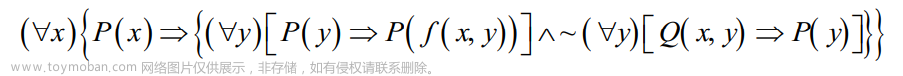浅谈反演-Toy模板网

这篇具有很好参考价值的文章主要介绍了浅谈反演。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

浅谈反演

二项式反演

\(g_i=\sum\limits_{j=0}\binom{i}{j}f_j,f_i=\sum\limits_{j=0}(-1)^{i-j}\binom{i}{j}g_j\)

还有一个的形式\(g_i=\sum\limits_{j=i}\binom{j}{i}f_j,f_i=\sum\limits_{j=i}(-1)^{i-j}\binom{j}{i}g_j\)

这里只针对第一个形式,为了得到更普遍的反演,这里我们引入一个等式

\(\sum\limits_{k=j}^{i}(-1)^{k-j}\binom{i}{k}\binom{k}{j}=[i=j]\)

注意到\(\binom{i}{k}\binom{k}{j}=\binom{i}{j}\binom{i-j}{k-j}\)

即\(\sum\limits_{k=j}^{i}(-1)^{k-j}\binom{i}{k}\binom{k}{j}=\binom{i}{j}\sum\limits_{k=j}^{i}(-1)^{k-j}\binom{i-j}{k-j}=\binom{i}{j}\sum\limits_{k=0}^{i-j}(-1)^{k}\binom{i-j}{k}=\binom{i}{j}(1-1)^{i-j}\)

这里只有\(i=j\)时\(0^0=1\)

定义矩阵\(A,B\),\(a_{i,j}=\binom{i}{j},b_{i,j}=(-1)^{i-j}\binom{i}{j}\)

\(A\times B=C\),\(c_{i,j}=\sum\limits_{k=0}^na_{i,k}b_{k,j}=\sum\limits_{k=0}^n(-1)^{k-j}\binom{i}{k}\binom{k}{j}=[i=j]\),则\(C=I\)

这里我们再记\(F\)为一维行向量,\(G\)同理

\(F\times A=G\),则\(F\times A\times B=G\times B=F\)

斯特林反演

斯特林数

先是第二类

\(n\brace m\),表示\(n\)个不同元素分到\(m\)个有序集合的方案数

不难得到一个递推式

\(n\brace m\) \(=\) \(n-1\brace m\) \(\times m\) \(+\) \(n-1\brace m-1\)

也就是新开一个集合或者在现有的集合里放一个

\(Bell\)数\(B_n=\sum\limits_{m=0}^n\)\(n\brace m\)

考虑一个集合任意大小\(A\)的标号方案为\(|A|\)

则其\(EGF\)为\(A(x)=\dfrac{x}{1!}+\dfrac{x^2}{2!}...=e^x-1\)

则\(Bell\)数即为多个\(A\)的标号合并,即为\(SET_A=e^{e^x-1}\)

设\(f_m\)为固定\(m\)后\(n\brace m\)的\(EGF\)

则\(f_m=\dfrac{(e^x-1)^m}{m!}\)

第一类

\(n\brack m\),表示\(n\)个不同元素分成\(m\)个轮换的方案数

直观看就是集合内部同样有顺序

同样不难得出递推式

\(n\brack m\) \(=\) \(n-1\brack m\) \(\times (n-1)\) \(+\) \(n-1\brack m-1\)

这里我们也不难得出生成函数

考虑固定\(n\),记为\(f_n(x)\)
则\(f_n(x)=f_{n-1}(x)*(n-1)+f_{n-1}(x)*x=f_{n-1}(x)\times(x+n-1)\)

\(f_0(x)=1\)

既得\(f_n(x)=\prod\limits_{i=0}^{n-1}(x+i)\),这就是\(x\)的\(n\)次上升幂,记为\(x^{\overline{n}}\)

下降幂同理为\(x^{\underline{n}}=\prod\limits_{i=0}^{n-1}(x-i)\)

考虑\((-x)^{\overline{n}}=\prod\limits_{i=0}^{n-1}(-x+i)=(-1)^n\prod\limits_{i=0}^{n-1}(x-i)=(-1)^nx^{\underline{n}}\)即为上升幂和下降幂的转化

这里我们先只探讨单个\(x^{\overline{n}}\)的求法

考虑倍增\(x^{\overline{2n}}=x^{\overline{n}}(x+n)^{\overline{n}}\)

\(x^{\overline{n+m}}=x^{\overline{n}}(x+n)^{\overline{m}}\)

若已知\(f(x)\),对于\(f(x+n)\)

\(f(x+n)=\sum\limits_if_i(x+n)^i=\sum\limits_{i}f_i\sum\limits_{j=0}^ix^jn^{i-j}\binom{i}{j}\)

\(=\sum\limits_jx^j\sum\limits_{i=j}n^{i-j}\binom{i}{j}f_i=\sum\limits_j\dfrac{x^j}{j!}\sum\limits_{i=j}\dfrac{n^{i-j}}{(i-j)!}i!f_i\)

注意到这是个卷积的形式

考虑如果固定\(m\)的话,这里我们可以采用类似\(n\brace m\)的方式

对于一个轮换,其\(EGF\)\(A(x)=\sum\limits\dfrac{(i-1)!}{i!}x^i=\sum\limits\dfrac{x^i}{i}\)

同样\(n\brack m\)为\(SET_A=A^m(x)\)

斯特林反演

首先有个式子

\(m^n=\sum\limits_{k=0}^{m}\)\(n\brace k\)\(\binom{m}{k}k!\)

也就是在\(n\)个不同的小球放到\(m\)个不同的小盒中,可为空,同时我们可以枚举用了多少小盒

考虑\(x^{\underline{n}}=(-x)^{\overline{n}}(-1)^n=\sum\limits_{i=0}^n\)\(n\brack i\)\((-1)^{n-i}x^i\)

\(=\) \(\sum\limits_{i=0}^n\)\(n\brack i\)\((-1)^{n-i}\) \(\sum\limits_{k=0}^{i}\)\(i\brace k\)\(\binom{x}{k}k!\)和

\(=\) \(\sum\limits_{i=0}^n\)\(n\brack i\)\((-1)^{n-i}\) \(\sum\limits_{k=0}^i\)\(i\brace k\)\(x^{\underline{k}}\)

\(=\)\(\sum\limits_{k=0}^n\)\(x^{\underline{k}}\)\(\sum\limits_{i=k}^n\)\(n\brack i\)\((-1)^{n-i}\)\(i\brace k\)

注意到当\(k=n\)时,\(\sum\limits_{i=k}^n\)\(n\brack i\)\((-1)^{n-i}\)\(i\brace k\) =1,因此其他时候皆为\(0\)

即\(\sum\limits_{i=k}^n\)\(n\brack i\)\((-1)^{n-i}\)\(i\brace k\) \(=[k=n]\)

这同样可以用二项式反演里的方法定义矩阵,最后得

\(g_i=\sum\limits_{j=0}\)\(i\brace j\) \(f_j,f_i=\sum\limits_{j=0}(-1)^{i-j}\)\(i\brack k\)\(g_j\)

\(g_i=\sum\limits_{j=0}\)\(i\brack j\) \(f_j,f_i=\sum\limits_{j=0}(-1)^{i-j}\)\(i\brace k\)\(g_j\)

生成函数的一些推论

幂和

首先我们知道\(\sum\limits_{i=0}^ni^k\)是个\(k+1\)次多项式

\(\sum\limits_{i=0}^ni^k\)=\(\sum\limits_{i=0}^n\)\(\sum\limits_{j=0}^{i}\)\(k\brace j\)\(\binom{i}{j}j!\)

注意\(k\brace j\)的\(EGF\)为\(\dfrac{(e^x-1)^j}{j!}\)

\(\sum\limits_{i=0}^n\sum\limits_{j=0}^{i}\binom{i}{j}[x^k]k!(e^x-1)^j=[x^k]k!\sum\limits_{i=0}^n\sum\limits_{j=0}^{i}\binom{i}{j}(e^x-1)^j\)

注意到\(\sum\limits_{j=0}^{i}\binom{i}{j}(e^x-1)^j\)是一个二项式展开的形式

则其可化为\([x^k]k!\sum\limits_{i=0}^n(e^{xi})=[x^k]k!\dfrac{e^{x(n+1)}-1}{e^x-1}\)

回到\(\sum\limits_{i=0}^n\)\(\sum\limits_{j=0}^{i}\)\(k\brace j\)\(\binom{i}{j}j!\)=\(\sum\limits_{j=0}^{n}\)\(k\brace j\)\(\sum\limits_{i=j}^{n}\binom{i}{j}j!\)

注意到\(\sum\limits_{i=j}^{n}\binom{i}{j}=\binom{n+1}{j+1}\)

其可化为\(\sum\limits_{j=0}^{n}\)\(k\brace j\)\(j!\binom{n+1}{j+1}\)

幂和变形

如果这里求的是\(\sum\limits_{i=0}^ni^k\binom{n}{i}\)

即可化为\(\sum\limits_{i=0}^n\)\(\sum\limits_{j=0}^{i}\)\(k\brace j\)\(\binom{i}{j}j!\binom{n}{i}\)=\(\sum\limits_{j=0}^{n}\)\(k\brace j\)\(\sum\limits_{i=j}^{n}\binom{i}{j}j!\binom{n}{i}\)=\(\sum\limits_{j=0}^{n}\)\(k\brace j\)\(j!\binom{n}{j}\)\(\sum\limits_{i=j}^{n}\binom{n-j}{i-j}\)

注意到\(\sum\limits_{i=j}^{n}\binom{n-j}{i-j}=\sum\limits_{i=0}^{n-j}\binom{n-j}{i}=2^{n-j}\)

则原式可化为\(\sum\limits_{j=0}^{n}\)\(k\brace j\)\(j!\binom{n}{j}\)\(2^{n-j}\),时间复杂度为\(\Theta(n\log_2n)\)

不过这里有线性做法

首先有复合函数\([x^k]F(G(x))\)

我们知道\(F(G(x))=\sum\limits_{i=0}[x^i]F(x)G^i(x)\),所以\([x^k]F(G(x))=[x^k]\sum\limits_{i=0}[x^i]F(x)G^i(x)\)

注意到如果\(G(x)\)的常数项为\(0\),\(i>k\)时对答案没贡献,因此我们的求和上限为\(k\)

回到本题,我们已经求的\(\sum\limits_{i=0}^ni^k=[x^k]k!\sum\limits_{i=0}^n(e^{xi})\)

注意到\(\binom{n}{i}\)的生成函数为\((1+x)^n\)

不难得出原式为\(\sum\limits_{i=0}^ni^k\binom{n}{i}=[x^k]k!\sum\limits_{i=0}^n[x^i](1+x)^n(e^{xi})\)

这个长得很像复合函数的展开,我们不难得出其为\([x^k]k!(1+e^x)^n\),这里有点不对,因为它的求和上限为\(+\infin\),但因为\(i>n\),\((1+x)^n\)的没有\(>n\)的项,所以求和上限可以改为\(n\)这里不难看出实际上是一个二项式展开

可上限为\(n\)依旧不行,因此我们想对\(G(x)=e^x\)去除常数项,也就是\(G(x)-1=e^x-1\)

原式即可化为\([x^k]k!\sum\limits_{i=0}^k[x^i](2+x)^n(e^x-1)^i\)

注意到我们这里并不处理\((e^x-1)^i\)

假设现在我们有一个函数\(F(x)\),我们考虑在\(x^k\)的地方截断,即\(f(x)=(F(x))\bmod(x^{k+1})\)

考虑\(F(x)\)向右平移\(c\)个单位,记为\(G(x)=F(x-c)\)

同样\(g(x)=f(x-c)\)

不难发现\([x^k]G(e^x)=[x^k]F(e^x-1)=[x^k]f(e^x-1)=[x^k]g(e^x)\)

其实这个好像不呢么显然

首先明确\(G(x)\not=g(x)\bmod x^{k+1}\)

举个例子

这里我们令\(c=1,G(x)=(x+1)^n\)

我们这里先回顾一下\(F(x)=(x+2)^n\)

\(f(x)=(x+2)^n \bmod x^{k+1}=\sum\limits_{i=0}^k\binom{n}{i}x^i2^{n-i}\)

\(g(x)=f(x-1)=\sum\limits_{i=0}^k\binom{n}{i}(x-1)^i2^{n-i}=\sum\limits_{i=0}^k\binom{n}{i}2^{n-i}\sum\limits_{j=0}^ix^j\binom{i}{j}(-1)^{i-j}=\sum\limits_{j=0}^kx^j\sum\limits_{i=j}^k\binom{n}{i}2^{n-i}\binom{i}{j}(-1)^{i-j}\)

\(G(x)=F(x-1)=\sum\limits_{i=0}^n\binom{n}{i}(x-1)^i2^{n-i}=\sum\limits_{j=0}^kx^j\sum\limits_{i=j}\binom{n}{i}2^{n-i}\binom{i}{j}(-1)^{i-j}\bmod x^{k+1}\)

明显\(g(x)\not=G(x)\bmod x^{k+1}\),但当\(j=k\)时,两者相等??注意这里\(x\)是不满足的

我们可以发现问题在于\(F(x-1)\)依旧有常数项,所以在截断和平移时会产生问题即\(f(x)\not =g(x+1)\bmod x^{k+1}\)

对于\(H(P(x))=[x^k]\sum\limits_{i=0}x^iH(x)P^i(x)\)

如果\(P(x)\)无常数项,则求和上限为\(k\)

因此我们可以直接截断,这里\(G(e^x)\bmod x^{k+1}=g(e^x)\),原因就在这

原式\(=\)\([x^k]k!G(e^x)=[x^k]k!F(e^x-1)=[x^k]k!f(e^x-1)=[x^k]k!g(e^x)\)

因此这里我们直接展开得到\([x^k]k!\sum\limits_{i=0}^k[x^i]g(x)e^{xi}\)

这里我们不妨把\([x^k]k!\sum\limits_{i=0}^ke^{xi}\)重新代为\(\sum\limits_{i=0}^ni^k\)

则原式可直接化为\(\sum\limits_{i=0}^k[x^i]g(x)i^k\)

注意到我们这里求和上限为\(k\),瓶颈在于\([x^i]g(x)\)

因此没有一个可以简单求得\(g(x)\)的方法

我们这里先明确\(G(x+1)=g(x+1)\bmod x^{k+1}\)，不过这里在推的时候还得借用\(f,F\)

首先对\(F\)求导,\(nF(x)=(x+2)F'(x)\)

这里我们可以直接将其替换\(f\),但要注意\(f'(x)\)的第\(k\)项缺失

即\(nf(x)=(x+2)f'(x)+2[x^k]F'(x)x^k\)

\(nf(x)-(x+2)f'(x)=2[x^k]F'(x)x^k\)

这里我们再平移一位

即\(ng(x)-(x+1)g'(x)=2[x^k]F'(x)(x-1)^k=n2^{n-k}\binom{n-1}{k}(x-1)^k\)

注意到\((x-1)^k\)可以展开

即\(ng(x)-(x+1)g'(x)=\sum\limits_{i=0}^kx^i\binom{k}{i}(-1)^{k-i}n2^{n-k}\binom{n-1}{k}\)

这里我们提取\(x^i\)的系数

则\(n[x^i]g(x)-[x^i](x+1)g'(x)=\binom{k}{i}(-1)^{k-i}n2^{n-k}\binom{n-1}{k}\)

\(n[x^i]g(x)-[x^i]g'(x)-[x^{i-1}]g'(x)=\binom{k}{i}(-1)^{k-i}n2^{n-k}\binom{n-1}{k}\)

还原\(g'(x)\),这里只需还原\(x^i,x^{i-1}\)即可

\(n[x^i]g(x)-(i+1)[x^{i+1}]g(x)-(i)[x^{i}]g(x)=\binom{k}{i}(-1)^{k-i}n2^{n-k}\binom{n-1}{k}\)

则\([x^{i+1}]g(x)=\dfrac{\binom{k}{i}(-1)^{k-i+1}n2^{n-k}\binom{n-1}{k}+(n-i)[x^i]g(x)}{i+1}\)

现在我们只需要求得\([x^0]g(x)\)即可

不难发现\([x^0]g(x)=\sum\limits_{i=0}^k\binom{n}{i}2^{n-i}(-1)^{i}\)

#include<bits/stdc++.h>
using namespace std;
const int MAXN=5005;
const int MOD=1e9+7;
int n,k;
int cnt_prime;
int Pow(int a,int b,int p)
{
    int base=a;
    int res=1;
    while(b)
    {
        if(b&1)
        {
            res=((long long)res*base)%p;
        }
        base=((long long)base*base)%p;
        b>>=1;
    }
    return res;
}
int inv(int a,int p)
{
    return Pow(a,p-2,p);
}
int inv_fac[MAXN];
int fac[MAXN];
int C(int n,int m)
{
    if(n<m||m<0)
    {
        return 0;
    }
    if(n==m||m==0)
    {
        return 1;
    }
    return ((((long long)fac[n]*inv_fac[m])%MOD)*inv_fac[n-m])%MOD;
}
int g[MAXN];
int main()
{
    int inv2=MOD-MOD/2;
    fac[0]=1;
    for(int i=1;i<=MAXN-5;i++)
    {
        fac[i]=((long long)fac[i-1]*i)%MOD;
    }
    inv_fac[MAXN-5]=inv(fac[MAXN-5],MOD);
    for(int i=MAXN-5-1;i>=1;i--)
    {
        inv_fac[i]=((long long)inv_fac[i+1]*(i+1))%MOD;
    }
    scanf("%d %d",&n,&k);
    if(n<=k)
    {
        int Res=0;
        for(int i=1;i<=n;i++)
        {
            int Ne=((long long)C(n,i)*Pow(i,k,MOD))%MOD;
            Res=((long long)Res+Ne)%MOD;
        }
        printf("%d\n",Res);
        return 0;
    }
    g[0]=0;
    int Mu2=Pow(2,n,MOD);
    int Bin=1;
    for(int i=0;i<=k;i++)
    {  
        int K=((long long)Mu2*Bin)%MOD;
        //printf("%d %d %d??\n",i,Mu2,Bin);
        if(i&1)
        {
            g[0]=((long long)g[0]-K+MOD)%MOD;
        }
        else
        {
            g[0]=((long long)g[0]+K)%MOD;
        }
        Mu2=((long long)Mu2*inv2)%MOD;
        Bin=((long long)Bin*(n-i))%MOD;
        Bin=((long long)Bin*inv(i+1,MOD))%MOD;
    }
    //printf("%d??\n",g[0]);
    int Ml=Pow(2,n-k,MOD);
    Ml=((long long)Ml*n)%MOD;
    int Kp=1;
    for(int i=0;i<k;i++)
    {
        Kp=((long long)Kp*(n-1-i))%MOD;
        Kp=((long long)Kp*inv(i+1,MOD))%MOD;
    }
    Ml=((long long)Ml*Kp)%MOD;
    for(int i=1;i<=k;i++)
    {
        int Kp=((long long)Ml*C(k,i-1))%MOD;
        if((k-(i-1)+1)&1)
        {
            Kp=MOD-Kp;
        }
        int Pp=(n-(i-1));
        Pp=((long long)Pp*g[i-1])%MOD;
        Kp=((long long)Kp+Pp)%MOD;
        Kp=((long long)Kp*inv(i,MOD))%MOD;
        g[i]=Kp;
    }
    int Res=0;
    for(int i=0;i<=k;i++)
    {
        int Ne=((long long)g[i]*Pow(i,k,MOD))%MOD;
        Res=((long long)Res+Ne)%MOD;
    }
    printf("%d\n",Res);
}

还有一个\(\sum\limits_{i=1}^nfab_i\times i^k\)

首先\(fab_i=fab_{i-1}+fab_{i-2}\)

不难得出\(fab\)的\(OGF\),\(f(x)=xf(x)+x^2f(x)+[x^0]f(x)\)

的解出\(f(x)=\dfrac{1}{1-x-x^2}\)

返回原式\([x^k]k!\sum\limits_{i=1}^n[x^i]\dfrac{1}{1-x-x^2} (e^{xi})\)

同样的套路令\(F(x)=\dfrac{1}{1-x-x^2}\),\(G(x)=e^x\)

则原式可化为\([x^k]k!\dfrac{1}{1-e^x-e^{2x}}\)(??),这里的求和上限为\(+\infin\),\(>n\)的项是会统计的

重新定义\(F,G\)

这里我们可以对\(G(x)\)截断,即\(G(x)=\dfrac{1}{1-x-x^2}\bmod x^{n+1}\)

原式即可化为\([x^k]k!\sum\limits_{i=1}^n[x^i]G(x) (e^{xi})=[x^k]k!G(e^x)\)

为了消除常数项,设\(G(x)=F(x-1)\),则其可化为\([x^k]k!F(e^x-1)\)

展开\([x^k]k!\sum\limits_{i=1}^n[x^i]F(x)(e^x-1)^i\),这里没有常数项,即\([x^k]k!\sum\limits_{i=1}^k[x^i]F(x)(e^x-1)^i\)

考虑对\(F(x)\)截断为\(f(x)=F(x)\bmod x^{k+1}\),原式可化为\([x^k]k!\sum\limits_{i=1}^k[x^i]f(x)(e^x-1)^i\)

我们在记\(g(x)=f(x-1)\),和上题一样,\(G(e^x)=g(e^x)\bmod x^{k+1}\)则原式可直接化为\(\sum\limits_{i=0}^k[x^i]g(x)i^k\)

这里\(F(x)=G(x+1)=\dfrac{1}{1-(x+1)-(x+1)^2}\bmod x^{n+1}=\dfrac{-1}{x^2+3x+1}\bmod x^{n+1}\)

注意这样是不对的,\(x^2+3x+1\)可能会往后贡献

我们先考虑\(G(x)=\dfrac{1}{1-x-x^2}\bmod x^{n+1}\)是什么

如果没有截断,\(G(x)=xG(x)+x^2G(x)+1\),不难发现,这里多算了\(fab_{n}x^{n+1}\),\(fab_{n}x^{n+2},fab_{n-1}x^{n+1}\)

即\(G(x)=xG(x)+x^2G(x)+1-fab_{n}x^{n+1}-fab_{n}x^{n+2}-fab_{n-1}x^{n+1}\)

则\(G(x)=\dfrac{1-fab_{n}x^{n+1}-fab_{n}x^{n+2}-fab_{n-1}x^{n+1}}{1-x-x^2}\)

则\(F(x)=\dfrac{fab_{n}(x+1)^{n+1}+fab_{n}(x+1)^{n+2}+fab_{n-1}(x+1)^{n+1}-1}{x^2+3x+1}\)

我们先明确,要递推求\(g\)

其中\(G(x+1)=g(x+1)\bmod x^{k+1}\)

我们知道\(G(x)\not =F(x-1)\bmod x^{k+1}\),但\(g(x)=f(x-1)\bmod x^{k+1}\)

因此我们可以先求得\(G(x+1)\bmod x^{k+1}\)

\(G(x+1)=F(x)=F(x)=\dfrac{fab_{n}(x+1)^{n+1}+fab_{n}(x+1)^{n+2}+fab_{n-1}(x+1)^{n+1}-1}{x^2+3x+1}\)

不妨令\(P(x+1)=fab_{n}(x+1)^{n+1}+fab_{n}(x+1)^{n+2}+fab_{n-1}(x+1)^{n+1}-1\)

则\(G(x+1)=\dfrac{P(x+1)}{x^2+3x+1}\)

则\(G(x+1)x^2+3xG(x+1)+G(x+1)=P(x+1)\)

这里我们求\(P(x+1)\)在\(x^{k+1}\)处截断的结果,令其为\(p(x+1)\)

我们再令\(h_n(x+1)=(x+1)^n\bmod x^{k+1}\)

\(P(x+1)=fab_{n}(x+1)^{n+1}+fab_{n}(x+1)^{n+2}+fab_{n-1}(x+1)^{n+1}-1\)

可以发现这里我们直接替换即可

即\(p(x+1)=(fab_n+fab_{n-1})h_{n+1}(x+1)+fab_nh_{n+2}(x+1)-1\)

对于\(h_n(x+1)\),求个导

\(h_n'(x+1)\times (x+1)+([x^k]h_n(x+1)-[x^{k-1}](h'_n(x+1)))x^k=nh_n(x+1)\)

即\(h'(x+1)\times(x+1)+(n\binom{n}{k}-n\binom{n-1}{k-1})x^k=nh_n(x+1)\)

则\(h'(x+1)\times(x+1)=nh_n(x+1)+(n-k)\binom{n}{k}x^k\)

提取\([x^i]\)的系数

\([x^i]h'(x+1)(x+1)=[x^i]nh_n(x+1)+[k=i](n-k)\binom{n}{k}\)

即\([x^{i-1}]h_n'(x+1)+[x^i]h_n'(x+1)=[x^i]nh_n(x+1)+[k=i](n-k)\binom{n}{k}\)

即\([x^{i}](i)h_n(x+1)+[x^{i+1}](i+1)h_n(x+1)=[x^i]nh_n(x+1)+[k=i](n-k)\binom{n}{k}\)

则\([x^i]h_n(x+1)=\dfrac{(n-i)[x^i]h_n(x+1)+[k=i](n-k)\binom{n}{k}}{i+1}\)

等等,\((x+1)^n\bmod x^{k+1}\)不是可以直接算吗???

设不取模的为\(H_n(x)\)

\(H_n(x)=x^n,H_n(x+1)=(x+1)^n,h_n(x+1)=\sum\limits_{i=0}^k\binom{n}{i}x^k,h_n(x)=\sum\limits_{i=0}^k\binom{n}{i}(x-1)^k\)

感觉推\(x+1\)没用吧,可能是我没理解

对不起,好像有用

直接沿用上一题的思路

\(G(x+1)x^2+3xG(x+1)+G(x+1)=P(x+1)\)

我们考虑截断\(x^{k+1}\)

\(g(x+1)x^2+3xg(x+1)+g(x+1)=p(x+1)+[x^{k}]g(x+1)(x)^{k+2}+[x^{k-1}]g(x+1)x^{k+1}+3[x^k]g(x+1)x^{k+1}\)

平移一下

\(g(x)(x-1)^2+3(x-1)g(x)+g(x)=p(x)+[x^{k}]g(x+1)(x-1)^{k+2}+[x^{k-1}]g(x+1)(x-1)^{k+1}+3[x^k]g(x+1)(x-1)^{k+1}\)

\(x^2g(x)+xg(x)-g(x)=p(x)+[x^{k}]g(x+1)(x-1)^{k+2}+[x^{k-1}]g(x+1)(x-1)^{k+1}+3[x^k]g(x+1)(x-1)^{k+1}\)

提取\([x^i]\)的系数

\([x^{i-2}]g(x)+[x^{i-1}]g(x)-[x^{i}]g(x)\)

\(=[x^i]p(x)+[x^k]g(x+1)(-1)^{k+2-i}\binom{k+2}{i}+[x^{k-1}]g(x+1)(-1)^{k+1-i}\binom{k+1}{i}+3[x^k]g(x+1)(-1)^{k+1-i}\binom{k+1}{i}\)

现在问题在于求\([x^i]p(x)\)

\(P(x+1)=fab_{n}(x+1)^{n+1}+fab_{n}(x+1)^{n+2}+fab_{n-1}(x+1)^{n+1}-1\)

\(p(x+1)=(fab_n+fab_{n-1})h_{n+1}(x+1)+fab_nh_{n+2}(x+1)-1\)

平移

\(p(x)=(fab_n+fab_{n-1})h_{n+1}(x)+fab_nh_{n+2}(x)-1\)

问题在于求\(h_{n}(x)\)

前面不是有\(h'(x+1)\times(x+1)=nh_n(x+1)+(n-k)\binom{n}{k}x^k\)

我们考虑在这里平移

\(h_n'(x)\times(x)=nh_n(x)+(n-k)\binom{n}{k}(x-1)^k\)

提取\([x^i]\)的系数

\([x^{i-1}]h'_n(x)=n[x^i]h_n(x)+(n-k)\binom{n}{k}(-1)^{k-i}\binom{k}{i}\)

\([x^{i}]ih_n(x)=n[x^i]h_n(x)+(n-k)\binom{n}{k}(-1)^{k-i}\binom{k}{i}\)

\([x^i]h_n(x)=\dfrac{(n-k)\binom{n}{k}(-1)^{k-i+1}\binom{k}{i}}{n-i}\)

至于\([x^k]g(x+1)\)如何求这里我们不妨用\(bostan-mori\)

代码似乎不好打就咕了

小结

对于\(\sum\limits_{i=0}^{n}[x^i]f(x)g^i(x)=f(g(x))=h(x)\)

我们可以利用平移\(g(x)\)来消除常数项,因此式子的求和上限变为\(k\)

也就是\(G(x+c)=g(x+c)\bmod x^{k+1}\),这里我们可以认为是先平移再截断再还原

但这样\(g(x)\)的求解变得异常复杂,可以利用求导等方式错位求解

单位根反演

我们称\(w^n=1\)为\(n\)次单位根

则\(w^n_k=e^{\frac{2k\pi i}{n}}\)

单位根反演即为\([n|k]=\dfrac{\sum\limits_{i=0}^{n-1}w^{ik}_n}{n}\)

似乎很显然,\(\dfrac{\sum\limits_{j=0}^{n-1}w^{jk}_n}{n}=\dfrac{\sum\limits_{j=0}^{n-1}e^{\frac{2kji\pi}{n}}}{n}\)

注意这是个等比数列,原式可化为,\(\dfrac{\dfrac{e^{2ki\pi}-1}{e^{\frac{2ki\pi}{n}}-1}}{n}\)

注意到\(e^{2ki\pi}-1=0\),只有当\([n|k]\)时分母也为\(0\)

因此\([n|k]=\dfrac{\sum\limits_{i=0}^{n-1}w^{ik}_n}{n}\)

逝一逝1

\(\sum\limits_{i=0,k|i}^n\binom{n}{i}\bmod (P=998244353)=\sum\limits_{i=0}^n[k|i]\binom{n}{i}=\sum\limits_{i=0}^n\frac{\sum\limits_{j=0}^{k-1}w_k^{ij}}{k}\binom{n}{i}=\frac{\sum\limits_{j=0}^{k-1}(w_k^j+1)^n}{k}\)

这里的\(w_k^j\)代原根即可

逝一逝2

如果这里的\(P\)无原根,这里的\(k\)是\(2\)的幂次

其实也差不多的,注意到我们发现\(f(x)=(x+1)^n\),这里我们就是求点值表示,直接任意模数\(NTT\)

其实对于大部分\(\sum\limits_{i=0,k|i}^n[x^i]f(x)\)似乎都可以这么做,\(n\)是\(f(x)\)的最高次

\(\sum\limits_{i=0}^n[k|i][x^i]f(x)=\sum\limits_{i=0}^n\frac{\sum\limits_{j=0}^{k-1}w_k^{ij}}{k}[x^i]f(x)=\frac{1}{k}\sum\limits_{j=0}^{k-1}f(w_k^j)\)

逝一逝3

\(\sum\limits_{i=0}^n[k|i]\binom{n}{i}fab_i\)

首先明确一点,对于矩阵\(A\)同样是满足二项式定理的

则原式化成\(\sum\limits_{i=0}^n[k|i]\binom{n}{i}A^i\)

然后再化成\(\sum\limits_{i=0}^n\frac{\sum\limits_{j=0}^{k-1}w_k^{ij}}{k}\binom{n}{i}A^i=\dfrac{1}{k}\sum\limits_{j=0}^{k-1}(w_k^jA+I)^n\)文章来源地址https://www.toymoban.com/news/detail-445392.html

到了这里，关于浅谈反演的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！