这篇具有很好参考价值的文章主要介绍了重积分 | 第二类曲面积分投影法正负判断。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。
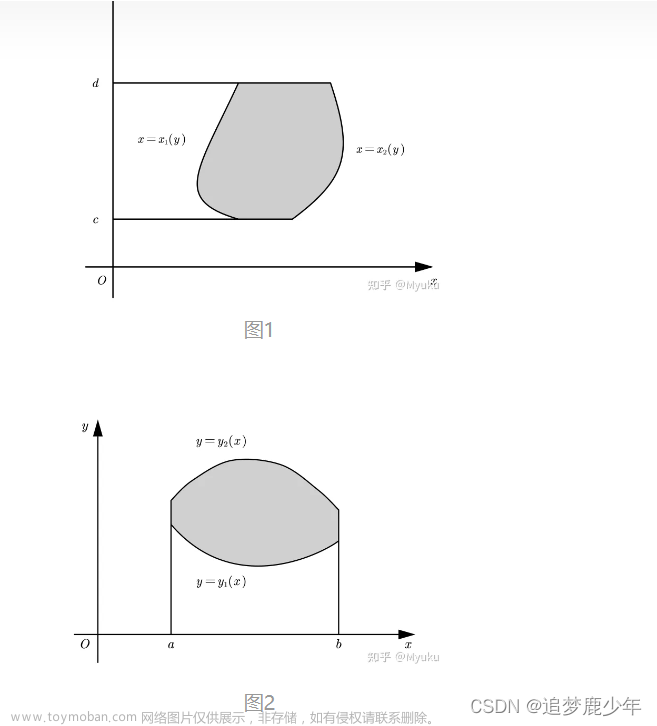
1，如果题目中要求的是外侧或者内侧
曲面是一张纸，假设外侧为白色，内侧为黑色
当选择外侧（白色）时，法向量与z正向为锐角
内侧（黑色）时，法向量与z正向为钝角
现假设曲面在桌子上方（z＞0）
投影就是把纸平铺在桌子上
可以发现，不管你在曲面的时候选择内侧还是外侧（白或黑），投影到桌子上的时候，展现出来的都是白色。
如过我之前选择的是内侧（黑色），此时就要加个负号
（把纸翻过来），来保证投影后的颜色与我之前选择的相同
2，如果题目中是上侧或者下侧，
就直接上侧取正，下侧取负。
原理跟上面举例的一样
摘自文章来源：https://www.toymoban.com/news/detail-445428.html
第二类曲面积分用投影法求的时候正负怎么判断？ - 知乎文章来源地址https://www.toymoban.com/news/detail-445428.html
到了这里，关于重积分 | 第二类曲面积分投影法正负判断的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！
依旧是公式极其复杂恶心的一章，建议是： 掌握两种线面积分的计算套路即可 ，和第8章一样属于同济版教材中最不重要的章节，不会对底层理解做过多考察~ 1.弧长曲线积分的几何意义 2.弧长曲线积分的定义和性质 3.弧长曲线积分的计算方式 4.坐标曲线积分的几何意义 5.坐标
提示：本文的适用对象为已修过《微积分A1》的非数学系学生，文中题型方法为个人总结，为个人复习使用。部分理解虽然不太严谨，但对于解题的实用性较强。若有疏漏or错误，欢迎批评指正。 对于已经熟知第一型曲线积分和第一型曲面积分定义的朋友们来说，我在这里主
🎈 算法并不一定都是很难的题目，也有很多只是一些代码技巧，多进行一些算法题目的练习，可以帮助我们开阔解题思路，提升我们的逻辑思维能力，也可以将一些算法思维结合到业务代码的编写思考中。简而言之，平时进行的算法习题练习带给我们的好处一定是不少的，
1：通过直插发光二极管的引脚长短来判断，脚长的是正极，脚短的是负极。 2：通过仔细观察管子内部的电极，较小的是正极，大的类似于碗状的是负极。 3：通过仪器万能表来判断：用红表笔接在发光二极管的正极，黑表笔接在发光二极管的负极，当发光二极管会正常发光
前置知识：黎曼积分的概念 介绍 由前置知识可得，黎曼积分可以求 x = a x=a x = a ， x = b x=b x = b ， x x x 轴和 y = f ( x ) y=f(x) y = f ( x ) 围成的图形， S = ∫ a b f ( x ) d x S=int_a^bf(x)dx S = ∫ a b f ( x ) d x 那么，我们就可以用这个方法来求平面区域的面积。 例题 设平面区域 D D D
1.连续曲线 y=f（x），f（x）＞＝0，与直线x=a，x=b围成的图形的面积。 2.连续曲线（x）在 a,b 上不都是非负的，则所为图形的面积。 设曲线与x轴的交点为c。 在 a，c 与 b，c 上微元形式不一样，分开分析。 3.上下两条曲线y=f₁（x）和y=f₂（x）与x=a和x=b所围成图形
前置知识：定积分求平面区域的面积 习题 设平面区域由曲线 y = x 2 − 1 y=x^2-1 y = x 2 − 1 和 y = − x 2 + 1 y=-x^2+1 y = − x 2 + 1 围成，求 D D D 的面积 S S S 解： qquad 两曲线的交点为点 ( − 1 , 0 ) (-1,0) ( − 1 , 0 ) 和点 ( 1 , 0 ) (1,0) ( 1 , 0 ) ，由此可得 S = ∫ − 1 1 [ ( − x 2 + 1 ) − (
考虑夹在垂直于 x x x 轴的两个(立体空间)平面 x = a x=a x = a 和 x = b x=b x = b , ( a b ) (ab) ( a b ) 之间的立体 V V V 的体积(其体积也不妨记为 V V V ) 假定 [ a , b ] [a,b] [ a , b ] 内任何一点处作垂直于 x x x 轴的平面截立体V的面积为 A ( x ) A(x) A ( x ) ,且 A ( x ) A(x) A ( x ) 是一个连续函数(为
1.求一段曲线与x 轴和任一直线、曲线围成的图形和极坐标下曲线围成的图形面积(求一块平面区域的面积) (1) x-型区域、 y-型区域介绍 极坐标： 设在平面直角坐标系上有一段曲线 y=f(x)0, a ≤ x ≤ b a leq x leq b a ≤ x ≤ b .我们在区间[a,b] 上取一个微元区间[x,x+dx] ,则此微段所对
正交变换是欧式空间保持向量内积不变的线性变换。不仅保持向量的长度不变，而且还保持向量 的夹角不变。二维或三维空间中的旋转变换、关于某一条直线或平面的对称变换都是正交变换．投影变换、平移变换不是正交变换． 正交变它从实内积空间 V V V 映射到 V V V 自 身
