数字图像处理——图像退化（大气湍流模型与运动模糊模型）与图像复原（逆滤波与维纳滤波）-Toy模板网

这篇具有很好参考价值的文章主要介绍了数字图像处理——图像退化（大气湍流模型与运动模糊模型）与图像复原（逆滤波与维纳滤波）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、图像退化

一般来说，图像的退化模型可以表示为
数字图像处理——图像退化（大气湍流模型与运动模糊模型）与图像复原（逆滤波与维纳滤波）

其中g(x,y) 表示退化后的图像，h(x,y)表示退化模型，f(x,y)表示原图像，n(x,y)表示噪声。
在频域上面可以表示为
数字图像处理——图像退化（大气湍流模型与运动模糊模型）与图像复原（逆滤波与维纳滤波）

下面介绍常见的两种退化模型：基于大气湍流物理特性的大气湍流模型和运动模糊模型。

1.大气湍流模型

退化模型：
数字图像处理——图像退化（大气湍流模型与运动模糊模型）与图像复原（逆滤波与维纳滤波）

伴随着k值的增大，得到的图像越来越模糊，一般情况下：k=0.0025剧烈湍流；k=0.001中等湍流；k=0.00025低湍流。
伪代码：
{
读取图片；
转成double型；
转换到频域空间；
频谱移到中心；

使用模型执行退化；
退化模型与原图像相乘求退化后图像；
进行傅里叶反变换即可。
}

代码如下：

%% 读取图像
image=imread('demo-1.jpg');
subplot(231);
imshow(image);
title('原图像');
f=im2double(image);
 
%% 剧烈大气湍流退化模型
F=fft2(f);%换到频域，信号在低频，噪声在高频
F=fftshift(F);%频谱移到矩阵中心
%执行
[W,H]=size(F);
[u,v]=meshgrid(1:W,1:H);%生成矩阵
H_turbulence=exp(-0.0025* ( (u-W/2).^2+(v-H/2).^2).^(5/6) );
F=F.*H_turbulence;
%傅里叶反变换
X=ifftshift(F);
turimg=ifft2(X);
turimg=uint8(abs(turimg)*256);
subplot(232);
imshow(turimg);
title('退化图像');

2.运动模糊模型

退化模型：
数字图像处理——图像退化（大气湍流模型与运动模糊模型）与图像复原（逆滤波与维纳滤波）

其中T=1, a=0.1, b=0.1。

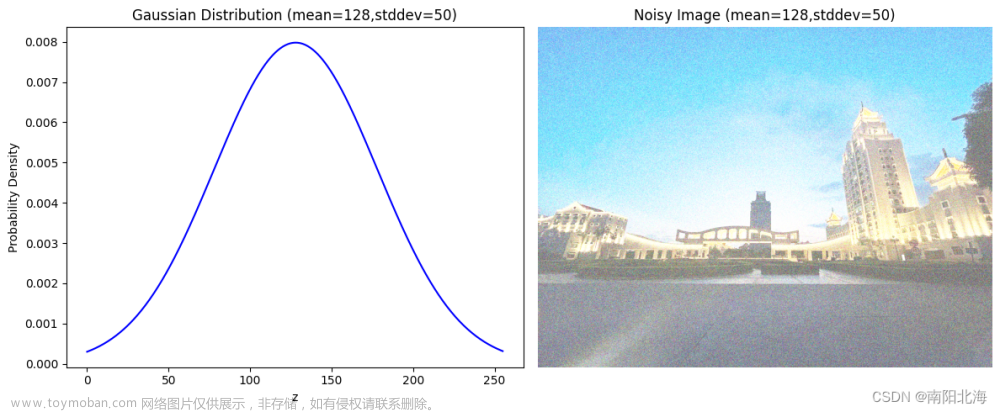
加性噪声——高斯噪声：

noise=imnoise(motion_blur,'gaussian',noise_mean,noise_var);
noise_mean=0，noise_var=0.01
代码如下：
pic=imread('demo-1.jpg'); 
figure('name','demo2');
subplot(231);imshow(pic);title('原图像');
pic=im2double(pic); 
[width,height]=size(pic);
%% 运动模糊（+噪声
H_motion = fspecial('motion', 28, 90);%运动长度为28，逆时针运动角度为90°
motion_blur = imfilter(pic, H_motion, 'conv', 'circular');%卷积滤波
noise_mean=0;  %添加均值为0
noise_var=0.001; %方差为0.001的高斯噪声
motion_blur_noise=imnoise(motion_blur,'gaussian',noise_mean,noise_var);
subplot(232);imshow(motion_blur,[]);title('运动模糊');
subplot(233);imshow(motion_blur_noise,[]);title('运动模糊加噪声');

二、图像复原

1.逆滤波

使用退化函数处理图像，然后加上适当的可加性噪声即可逆滤波实验。已获得退化函数后，用退化函数除退化图像的傅里叶变换计算原始图像傅里叶变换的估计：
数字图像处理——图像退化（大气湍流模型与运动模糊模型）与图像复原（逆滤波与维纳滤波）

即使知道退化函数，也不能准确的复原未退化的图像；如果退化函数是0或者是很小的值，噪声容
易被放大。
实现思路：
由于H(0,0)在频率域中通常是H(u, v)的最高值。因此，通过将频率限制在原点附近分析，就减少了遇
到零值的概率。
伪代码：
{
将信号频谱集中于低频区域，噪声集中于高频区域；
频谱移到矩阵中心；
以频谱中心为圆心，内部直接逆滤波，外部赋值为0
}
代码如下：

%% 逆滤波复原
fourier_H=fft2(H_motion,width,height);  %统一大小
fourier_degrade_img1=fft2(motion_blur);    %G(u,v)=H(u,v)F(u,v)，已知G(u,v),H(u,v)，求F(u,v)
restore_one=ifft2(fourier_degrade_img1./fourier_H); h=fspecial('gaussian',width,5);
restore_three=imfilter(restore_one,h,'conv','circular');
subplot(234);imshow(im2uint8(restore_three),[]);title('逆滤波+运动模糊');
 
fourier_degrade_img2=fft2(motion_blur_noise); %G(u,v)=H(u,v)F(u,v)+N(u,v)
restore_two=ifft2(fourier_degrade_img2./fourier_H);
restore_four=imfilter(restore_two,h,'conv','circular');
subplot(235);imshow(im2uint8(restore_four),[]);title('逆滤波+运动模糊加噪声');

2.维纳滤波

数字图像处理——图像退化（大气湍流模型与运动模糊模型）与图像复原（逆滤波与维纳滤波）

重点在于寻找信噪比。

代码如下：

%% 维纳滤波
fourier_H_motion=fft2(H_motion,width,height);  %H(u,v)
pow_H_motion=abs(fourier_H_motion).^2;   %|H(u,v)|^2
noise=motion_blur_noise-motion_blur;    %提取噪声分量
fourier_noise=fft2(noise);    % N(u,v)  噪声傅里叶变换
fourier_double_gray_pic=fft2(pic);  %F(u,v)为未经过退化的图片
nsr=abs(fourier_noise).^2./abs(fourier_double_gray_pic).^2;   %噪信比=|N(u,v)|^2/|F(u,v)|^2
H_w=1./fourier_H_motion.*pow_H_motion./(pow_H_motion+nsr); %H_w(u,v)=1/H(u,v)*|H(u,v)|^2/[|H(u,v)|^2+NSR] 
fourier_motion_blur_noise=fft2(motion_blur_noise);  %G(u,v)
restore_with_noise=ifft2(fourier_motion_blur_noise.*H_w);  %输出频域=G(u,v)H_w(u,v)，时域为频域傅里叶逆变换
subplot(236);imshow(restore_with_noise,[]);title('维纳滤波')

三、实现结果

数字图像处理——图像退化（大气湍流模型与运动模糊模型）与图像复原（逆滤波与维纳滤波）

四、附录

1.图片
demo-1.jpg
数字图像处理——图像退化（大气湍流模型与运动模糊模型）与图像复原（逆滤波与维纳滤波）
demo-2.jpg

myMatlab.m

clc;        
clear;       
close all;
%% 官方运动模糊+维纳滤波
I = im2double(imread('demo-1.jpg'));
figure,subplot(2,3,1),imshow(I);
title('原图');

%运动模糊
LEN = 28;
THETA = 90;
PSF = fspecial('motion', LEN, THETA);
blurred = imfilter(I, PSF, 'conv', 'circular');
subplot(2,3,2),imshow(blurred);
title('运动模糊退化');

wnr1 = deconvwnr(blurred, PSF, 0);
subplot(2,3,3),imshow(wnr1);
title('运动模糊复原');

%运动模糊+噪声
noise_mean = 0;
noise_var = 0.0001;
blurred_noisy = imnoise(blurred, 'gaussian', ...
                        noise_mean, noise_var);
subplot(2,3,4),imshow(blurred_noisy)
title('运动模糊+噪声')

wnr2 = deconvwnr(blurred_noisy, PSF, 0);
subplot(2,3,5),imshow(wnr2)
title('模糊+噪声 逆滤波');
signal_var = var(I(:));
wnr3 = deconvwnr(blurred_noisy, PSF, noise_var / signal_var);
subplot(2,3,6),imshow(wnr3)
title('模糊+噪声 维纳滤波');

mymotion.m

clc;         
clear;       
close all;   
pic=imread('demo-1.jpg'); 
figure('name','demo2');
subplot(231);imshow(pic);title('原图像');
pic=im2double(pic); 
[width,height]=size(pic);

%% 运动模糊（+噪声
H_motion = fspecial('motion', 28, 90);%运动长度为28，逆时针运动角度为90°
motion_blur = imfilter(pic, H_motion, 'conv', 'circular');%卷积滤波
noise_mean=0;  %添加均值为0
noise_var=0.001; %方差为0.001的高斯噪声
motion_blur_noise=imnoise(motion_blur,'gaussian',noise_mean,noise_var);
subplot(232);imshow(motion_blur,[]);title('运动模糊');
subplot(233);imshow(motion_blur_noise,[]);title('运动模糊加噪声');

%% 逆滤波复原
fourier_H=fft2(H_motion,width,height);  %变大小
fourier_degrade_img1=fft2(motion_blur);    % G(u,v)=H(u,v)F(u,v)，已知G(u,v),H(u,v)，求F(u,v)
restore_1=ifft2(fourier_degrade_img1./fourier_H);  % 
h=fspecial('gaussian',width,5);
restore_2=imfilter(restore_1,h,'conv','circular');
subplot(234);imshow(im2uint8(restore_2),[]);title('逆滤波+运动模糊');

fourier_degrade_img2=fft2(motion_blur_noise); %G(u,v)=H(u,v)F(u,v)+N(u,v)
restore_3=ifft2(fourier_degrade_img2./fourier_H);
restore_4=imfilter(restore_3,h,'conv','circular');
subplot(235);imshow(im2uint8(restore_4),[]);title('逆滤波+运动模糊加噪声');

%% 维纳滤波
fourier_H_motion=fft2(H_motion,width,height);  %H(u,v)
pow_H_motion=abs(fourier_H_motion).^2;   %|H(u,v)|^2
noise=motion_blur_noise-motion_blur;    %提取噪声分量
fourier_noise=fft2(noise);    % N(u,v)  噪声傅里叶变换
fourier_double_gray_pic=fft2(pic);  %F(u,v)为未经过退化的图片
nsr=abs(fourier_noise).^2./abs(fourier_double_gray_pic).^2;   %噪信比=|N(u,v)|^2/|F(u,v)|^2
H_w=1./fourier_H_motion.*pow_H_motion./(pow_H_motion+nsr); %H_w(u,v)=1/H(u,v)*|H(u,v)|^2/[|H(u,v)|^2+NSR] 
fourier_motion_blur_noise=fft2(motion_blur_noise);  %G(u,v)
restore_with_noise=ifft2(fourier_motion_blur_noise.*H_w);  %输出频域=G(u,v)H_w(u,v)，时域为频域傅里叶逆变换
subplot(236);imshow(restore_with_noise,[]);title('维纳滤波')

myturbulence.m文章来源地址https://www.toymoban.com/news/detail-445459.html

clc;
clear;
close all;
%% 读取图像
image=imread('demo-2.jpg');
subplot(231);
imshow(image);
title('原图像');
f=im2double(image);

%% 剧烈大气湍流退化模型
F=fft2(f);%换到频域，信号在低频，噪声在高频
F=fftshift(F);%频谱移到矩阵中心
%执行
[W,H]=size(F);
[u,v]=meshgrid(1:W,1:H);%生成矩阵
H_turbulence=exp(-0.0025* ( (u-W/2).^2+(v-H/2).^2).^(5/6) );
F=F.*H_turbulence;
%傅里叶反变换
X=ifftshift(F);
turimg=ifft2(X);
turimg=uint8(abs(turimg)*256);
subplot(232);
imshow(turimg);
title('大气湍流退化');

%% 直接逆滤波
FDeblurred=F./H;
IDeblurred=real(ifft2(ifftshift(FDeblurred)));
subplot(233), imshow(uint8(255.*mat2gray(IDeblurred)));
title('直接逆滤波');