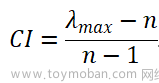基于AHP（层次分析法）确定权值的模糊综合评价-Toy模板网

这篇具有很好参考价值的文章主要介绍了基于AHP（层次分析法）确定权值的模糊综合评价。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

目录
1、模糊综合评价
2、权值的确定

一、模糊综合评价

因素集：影响评价的因素，例如:企业家的素质综合评价可以考虑5个因素{德，能，勤，绩，生命周期延长}
评价集：某因素好与坏，例如:企业家的德可以被评价为｛高较高一般低｝
单因素评价矩阵：rij代表因素i对评价j的隶属度。例如:企业家的德是较高的隶属度为0.7，可以认为企业家的德有0.7的程度是较高的。
各指标权重：各因素的重要程度，例如:有m个因素，权值向量A={a1,a2,….am}
模糊综合评价：通过模糊变换，将U上的向量A变换成V上的向量B。
基于AHP（层次分析法）确定权值的模糊综合评价
其中A为各因素权值，R为单因素评价矩阵，向量B为本次综合评价对评价集的隶属度。其中○称为综合评价合成算子,这里可以取为一般的矩阵乘法。
若评价集｛高较高一般低｝对应分数分别为S={100 80 60 40}

则F为总得分。基于AHP（层次分析法）确定权值的模糊综合评价

二、权值的确定

权值的确定有多种方法。熵权系数法，层次分析法（Analytic Hierarchy Process，AHP）是常用的几种方法，下面介绍层次分析法。

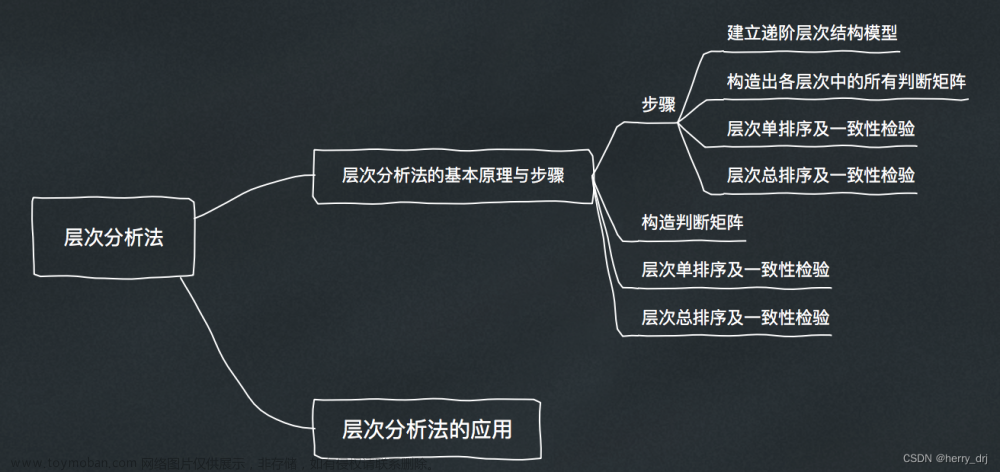
层次分析法包括三个步骤：
1、构造判断矩阵
2、用和积法计算权值（最大特征根对应的特征向量）
3、一致性检验

（1）构造判断矩阵

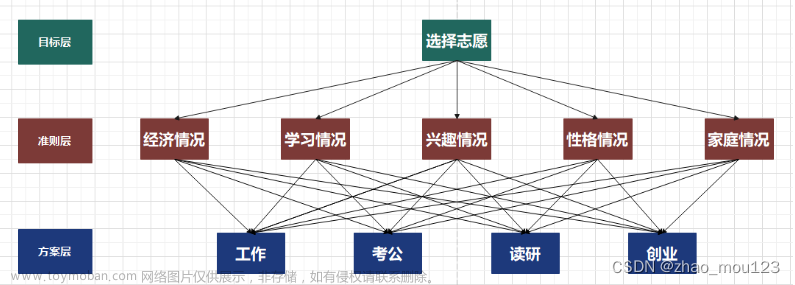
在深入分析问题的基础上，将决策的目标、考虑的因素和决策对象按相关关系分为最高层、中间层和最低层。
最高层：决策的目的、要解决的问题
中间层：主因素，考虑的因素、决策的准则
最低层：决策时的备选方案，也可为中间层的子因素基于AHP（层次分析法）确定权值的模糊综合评价
通过各因素两两比较构造判断矩阵Mij。
例如：因素i非常重要（9分），因素j稍微重要（3分）则mij=9/3=3即因素i相对因素j的重要性为3。一般地，满足

基于AHP（层次分析法）确定权值的模糊综合评价
的判断矩阵称为一致性矩阵。
（2）计算权值
对一致性矩阵，数学上可以证明对于其最大特征根对应的特征向量W。
有

而aij可以看做因素i对因素j的重要性，因此wi,wj可以看做因素i,因素j的绝对权值，经过归一化处理可以得到（一、模糊综合评价）中的权值。
（3）一致性检验
判断矩阵Mij一般不满足一致性，但是仍将其当做一致矩阵来处理，从而获得一组权重，但是这组权重能不能被接受，需要进行一致性检验。当CR<0.1时，认为判断矩阵的一致性是可以接受的，否则须要对判断矩阵作适当修正。

参考：
[1] PurePlayer. AHP | 层次分析法原理及Python实现https://zhuanlan.zhihu.com/p/108958590
[2] 00木水. 数模系列(3)：模糊综合评价法https://zhuanlan.zhihu.com/p/32666445
[3]房毅. 企业家素质模糊综合评价[J]. 淮海工学院学报：自然科学版, 2000, 9(2):5.文章来源地址https://www.toymoban.com/news/detail-445489.html

到了这里，关于基于AHP（层次分析法）确定权值的模糊综合评价的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！