数据结构学习笔记——图的遍历算法（深度优先搜索和广度优先搜索）-Toy模板网

这篇具有很好参考价值的文章主要介绍了数据结构学习笔记——图的遍历算法（深度优先搜索和广度优先搜索）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、图的遍历概念

图的遍历指从图中某一顶点出发（任意一个顶点都可以作为访问的起始顶点），按照某种遍历方法，对图中所有的顶点访问一次且只访问一次。图与树不一样，其中一个顶点可能与多个顶点相连，所以需记录已访问过的顶点，当访问一个顶点后，考虑如何选取下一个要访问的顶点。

图的遍历分为两种，深度优先搜索和广度优先搜索，这两种方法对无向图和有向图都适用。

二、深度优先搜索（DFS）

（一）DFS算法步骤

前面文章中，讲到过二叉树的先序遍历，其实这里图的深度优先搜索（DFS）是由其推广而来的。

二叉树的先序遍历中，首先是根结点，遍历完根结点的左子树，然后再遍历完根结点的右子树，依次下去至所有结点都遍历到。

图的深度优先遍历（DFS）需要借助栈来遍历：
①首先，选取图中某一顶点v_i作为起始点访问；
②任意选取一个与v_i邻接的顶点，且该顶点未被访问，一直重复下去，直到图中所有与v_i连通的顶点都被访问到；【可概括为由起始顶点开始，沿着一条路径尽可能地深入搜索该图，直到无法再继续下去】
③若还有顶点未被访问到，则另外选取一个未被访问的顶点再次作为起始点，回溯到上一个未访问的顶点，重复以上步骤，直至图中所有结点被访问。

可以看出DFS算法是一个递归过程，其中需借助栈完成操作。

1、邻接表DFS算法步骤

例如下面这个无向图：

数据结构学习笔记——图的遍历算法（深度优先搜索和广度优先搜索）
该图的邻接表如下：

通过邻接表进行深度优先搜索的步骤如下（以V1为访问起始点，不唯一）：
1、首先访问0，即V1，访问后标记已访问过；
2、查看V1单链表，第一个未访问的邻接顶点为2，即V3，并以V3为出发点继续深度遍历；
3、查看V3单链表，其第一个未访问的邻接顶点为6，即V7，再以V7为出发点继续深度遍历；
4、查看V7单链表，其邻接顶点为2，即V3，它已经被访问过，于是回到V3单链表，搜索下一个未被访问的邻接顶点；
5、查看V3单链表，其下一个未访问的邻接顶点为5，即V6，以V6为出发点继续深度遍历；
6、查看V6单链表，其邻接顶点为2，也是已经被访问过，于是回到V3单链表，搜索下一个未被访问的邻接顶点；
7、查看V3单链表，其邻接顶点为0，即V1，一开始被访问过，于是回到V1单链表，搜索下一个未被访问的邻接顶点；
8、查看V1单链表，其下一个未访问的邻接顶点为1，即V2，并以V2为出发点继续深度遍历；
9、查看V2单链表，其第一个未访问的邻接顶点为4，即V5，再以V5为出发点继续深度遍历；
10、查看V5单链表，其第一个未访问的邻接顶点为7，即V8，再以V8为出发点继续深度遍历；
11、查看V8单链表，其邻接顶点为4，即V5，已经被访问过，于是回到V5单链表，搜索下一个未被访问的邻接顶点；
12、查看V5单链表，其下一个未被访问的邻接顶点为1，即V2，于是回到V2单链表，搜索下一个未被访问的邻接顶点；
13、查看V2单链表，其邻接顶点为3，即V4，并以V4为出发点继续深度遍历；
14、查看V4单链表，其邻接顶点为7，即V8，再以V8为出发点继续深度遍历；
15、查看V8单链表，其邻接顶点为3，即V4，再以V4为出发点继续深度遍历；
16、查看V4单链表，其邻接顶点为1，即V2，再以V2为出发点继续深度遍历；
17、查看V2单链表，其邻接顶点为0，即V1，再以V1为出发点继续深度遍历；
18、查看V1单链表，其邻接顶点为2，即V3，V3中已经不存在未访问的顶点，于是回到V1单链表。
19、查看V1单链表，下一个邻接顶点为1，即V2，V2中已经不存在未访问的顶点，最后回到V1单链表，遍历完成。
故该图的深度优先遍历序列为：V1、V3、V7、V6、V2、V5、V8、V4。

2、邻接矩阵DFS算法步骤
通过图的邻接矩阵实现深度优先搜索，例如下面这个图（以V1为访问起始点，是唯一的）：

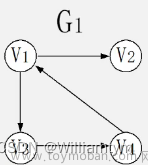
例如，对于下面这个有向图，对其进行深度优先搜索：

数据结构学习笔记——图的遍历算法（深度优先搜索和广度优先搜索）
其邻接矩阵如下：

1、由V1开始，如下表【第一行为回退点，第二行为深度优先搜索得到的序列】：


V1

2、通过其邻接矩阵知，访问第一行第二列的1对应的V2顶点，由于它是在V1的行中被访问到的，所以回退点为V1：

	V1
V1	V2

3、由于访问了V2，即开始访问V2行，访问第二行第三列的1对应的V4顶点，由于它是在V2的行中被访问到的，所以回退点为V2：

	V1	V2
V1	V2	V4

4、由于访问了V4，即开始访问V4行，访问第四行第五列的1对应的V5顶点，由于它是在V4的行中被访问到的，所以回退点为V4：

	V1	V2	V4
V1	V2	V4	V5

5、由于访问了V5，即开始访问V5行，由于第五行都为0，回退到V4，由于V4行顶点都访问完，回退到V2，由于V2行顶点都访问完，回退到V1行，此时V1行还剩第一行第三列的1对应的V3顶点未访问，访问该顶点：

	V1	V2	V4
V1	V2	V4	V5	V3

6、至此，访问完了图中的所有顶点，即深度优先搜索序列为V1、V2、V4、V5、V3。

对于深度优先搜索（DFS），由于基于邻接表的遍历得到的序列可能不是唯一的，即根据边的输入次序不同，从而得到的邻接表不同，从而遍历序列不一样；而基于邻接矩阵所得到的DFS遍历序列是唯一的。

写出下面这个图的深度优先遍历序列：

数据结构学习笔记——图的遍历算法（深度优先搜索和广度优先搜索）
其深度优先遍历序列为：0，4，6，9，8，7，5，3，2，1。

（二）DFS的空间复杂度和时间复杂度

对于一个图G=（V，E），由顶点集V和边集E组成。
1、DFS算法的空间复杂度
由于DFS算法是一个递归算法，即递归顶点集V，通过DFS遍历的空间复杂度为O(|V|)。

2、DFS算法的时间复杂度
时间复杂度取决于图的存储结构，若通过邻接矩阵表示图，则查找顶点的邻接顶点所需时间为O(|V|)，总时间复杂度为O(|V²|)（邻接矩阵为方阵n×n）；若通过邻接表表示图，则查找所有顶点的邻接顶点所需时间为O(|E|)，访问顶点所需时间为O(|V|)，即总时间复杂度为O(|V|+|E|)。

三、深度优先生成树（森林）

对一个连通图或非连通图进行DFS遍历后，若将在遍历过程中所经历过的顶点保留，则可以形成一棵树或森林，即深度优先生成树或深度优先生成森林；另外，基于邻接表存储的深度优先生成树或深度优先生成森林也是不唯一的；而对于邻接矩阵则是唯一的。

例如，上面这个无向连通图遍历DFS遍历生成的深度优先生成树如下（基于邻接表）：
数据结构学习笔记——图的遍历算法（深度优先搜索和广度优先搜索）
例如，对于上面这个有向图进行DFS遍历：

它并不是连通图，得到的深度优先生成森林如下：

四、广度优先搜索（BFS）

（一）BFS算法步骤

前面文章中，讲到过二叉树的层序遍历，其实这里图的广度优先搜索（BFS）是由其推广而来的。

二叉树的层序遍历中，层次优先，当对一层的结点都遍历完后，遍历下一层，按照次序对每个结点的左、右孩子进行遍历。

图的广度优先搜索（BFS）需要借助到队列来遍历：
①首先，选取图中某一顶点v_i作为出发点，访问后将其入队并标记为已访问（使用队列用于避免重复访问，存放已经访问过的各邻接顶点）；
②依次访问与v_i邻接的顶点，即当队列不为空时检查出队顶点的所有邻接顶点，访问未被访问的邻接顶点并将其入队，重复该过程；【可概括为由起始顶点开始，按照广度优先的顺序逐层遍历与当前顶点相邻的顶点将其访问】
③当队列为空时跳出循环，即所有已被访问的顶点的邻接顶点均被访问到，则此时遍历完成。

可以知道BFS算法并不是递归过程，且要用到队列。

1、邻接表BFS算法步骤
例如下面这个无向图：
数据结构学习笔记——图的遍历算法（深度优先搜索和广度优先搜索）
该图的邻接表如下：

通过邻接表进行广度优先搜索的步骤如下（这里以V1为访问起始点，不唯一）：
1、首先访问0，即V1，访问后标记已访问过，使其入队，然后删除当前队头结点；【V1】
2、遍历V1单链表，使其未访问的邻接顶点2、1入队并标记；【V2、V3】
3、访问队头结点1并删除，然后遍历1对应的V2单链表，使其未访问的邻接顶点4、3入队并标记；【V3、V4、V5】
4、访问队头结点2并删除，然后遍历2对应的V3单链表，使其未访问的邻接顶点6、5入队并标记；【V4、V5、V6、V7】
5、访问队头结点3并删除，然后遍历3对应的V4单链表，使其未访问的邻接顶点7入队并标记；【V5、V6、V7、V8】
6、访问队头结点4并删除，然后遍历4对应的V5单链表，该单链表中无未访问的顶点；【V6、V7、V8】
7、访问队头结点5并删除，然后遍历5对应的V6单链表，该单链表中无未访问的顶点；【V7、V8】
8、访问队头结点6并删除，然后遍历6对应的V7单链表，该单链表中无未访问的顶点；【V8】
9、访问队头结点7并删除，然后遍历7对应的V8单链表，该单链表中无未访问的顶点，此时队列为空，遍历结束；【】
故该图的深度优先遍历序列为：V1、V2、V3、V4、V5、V6、V7、V8。

2、邻接矩阵BFS算法步骤
通过图的邻接矩阵实现广度优先搜索，例如下面这个图（以V1为访问起始点，是唯一的）：

例如，对于下面这个有向图，对其进行广度优先搜索：

数据结构学习笔记——图的遍历算法（深度优先搜索和广度优先搜索）
其邻接矩阵如下：

1、由V1行开始，如下表：

V1

2、可得与其匹配的有V2、V3，填到表中V1之后：

V1	V2	V3

3、由V2行开始，其中V4未访问，填到V3之后：

V1	V2	V3	V4

4、由V3行开始，都为0，继续下一行。
5、由V4行开始，其中V5未访问，填到V4之后：

V1	V2	V3	V4	V5

6、至此，该图的所有顶点都已访问到，得到的序列便是广度优先搜索，即深度优先搜索序列为V1、V2、V3、V4、V5。

同样，对于广度优先搜索，由于基于邻接表的遍历得到的序列可能不是唯一的，即根据边的输入次序不同，从而得到的邻接表不同，从而遍历序列不一样；而基于邻接矩阵所得到的遍历序列是唯一的，这两点和深度优先搜索遍历是一样的。

（二）BFS的空间复杂度和时间复杂度

对于一个图G=（V，E），由顶点集V和边集E组成。
1、BFS算法的空间复杂度
通过BFS遍历的空间复杂度为O(|V|)。

2、BFS算法的时间复杂度
时间复杂度取决于图的存储结构，若通过邻接矩阵表示图，则查找顶点的邻接顶点所需时间为O(|V|)，总时间复杂度为O(|V²|)（邻接矩阵为方阵n×n），这和DFS算法的时间复杂度是一样的；若通过邻接表表示图，则每个顶点都入队一次，即所需时间为O(|V|)，搜索顶点的邻接顶点所需时间为O(|E|)，其时间复杂度为O(|V|+|E|)。