【数据结构】二叉树的创建和四种遍历（附带详细注释）-Toy模板网

这篇具有很好参考价值的文章主要介绍了【数据结构】二叉树的创建和四种遍历（附带详细注释）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

前言

《数据结构系列首页》是数据结构系列文章的首页，其中会逐步更新各种数据结构的实现，有兴趣的选手可以一看。
首页中不仅有各种数据结构的实现，还有学习数据结构必备的基础知识，如果有选手觉得自己的基础不太牢固，可以先将搞定基础知识，之后再攻克数据结构这一部分的内容。
由于我也是刚开始学习数据结构这门课程，所以如果发现文章中存在错误，希望大家可以直接指出，我将第一时间修改。
更多数据结构的实现请见《数据结构系列文章》，我会在学习完新的数据结构后不断更新其中的内容。

一、开场白

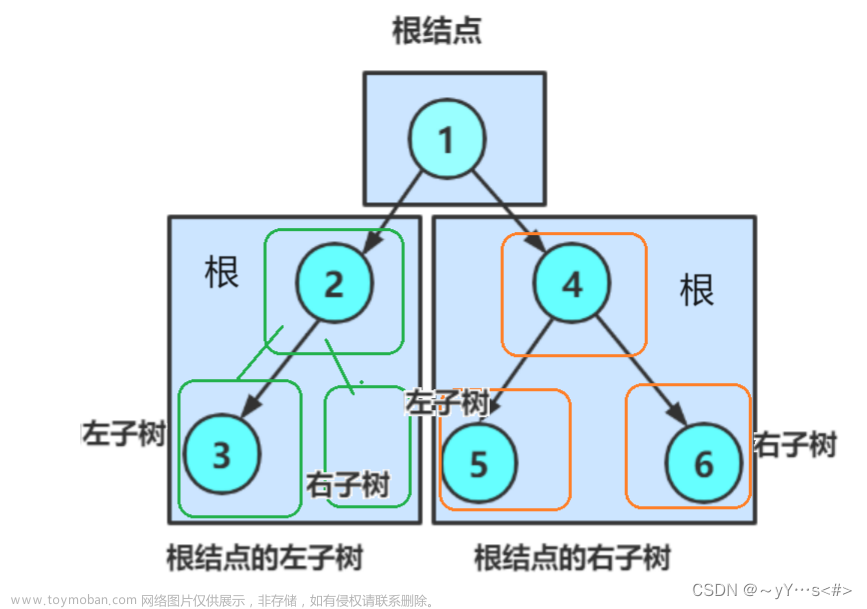
树是一种比起线性表更加复杂的存储结构，其是一种非常重要的非线性数据结构，树结构在客观世界中普遍存在，其中二叉树的运用最为广泛。本篇文章主要介绍了二叉树的链式存储结构（即二叉链表）的创建与遍历，这将为以后对二叉树的研究起到至关重要的作用。

二、二叉树结点的设计

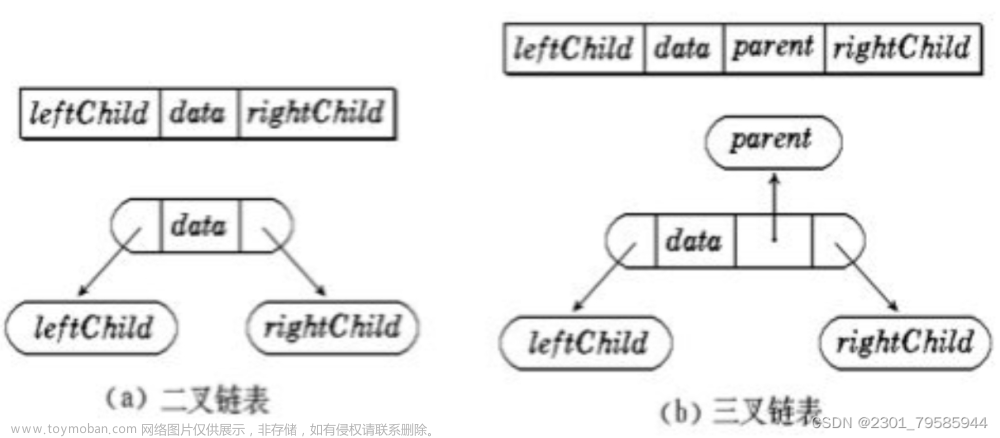
考虑到二叉树中的每个结点最多可以指向两个结点，所以为二叉树的结点设置一个数据域和两个指针域是非常自然的想法。

typedef char TreeElemType; // 定义二叉树的元素类型为字符类型

// 定义二叉树结点
typedef struct TreeNode
{
   
	TreeElemType data; // 数据域
	struct TreeNode* leftchild;  // 左指针域
	struct TreeNode* rightchild; // 右指针域
}TreeNode, * TREE; // TREE 等同于 struct TreeNode *

二叉树结点结构如下图所示：
【数据结构】二叉树的创建和四种遍历（附带详细注释）

三、二叉树的遍历

先序遍历

先序遍历规则

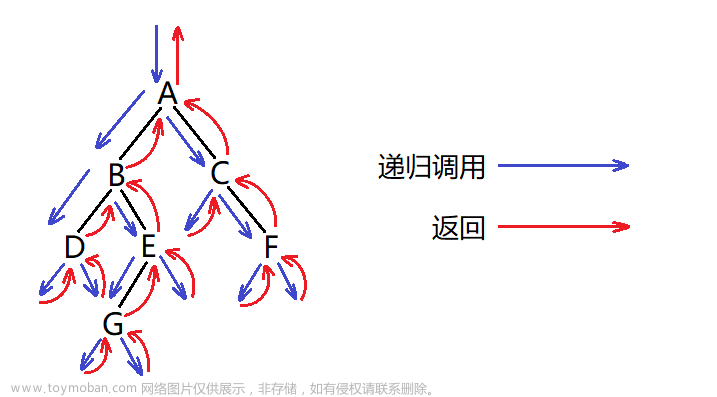
若二叉树为空，则不进行遍历；否则先访问根结点，然后前序遍历左子树，再前序遍历右子树。如下图所示，先序遍历的结果为ABDGHCEIF。由遍历结果可知，先序遍历属于深度优先遍历，即优先向树的最深处探索。
【数据结构】二叉树的创建和四种遍历（附带详细注释）

先序遍历递归算法

void pre_order_traverse(TREE T)
{
   
	if (T) // T为空是递归结束的条件
	{
   
		putchar(T->data); // 打印根结点的数据
		pre_order_traverse(T->leftchild);  // 先序遍历左子树
		pre_order_traverse(T->rightchild); // 先序遍历右子树
	}
}

中序遍历

中序遍历规则

若二叉树为空，则不进行遍历；否则先中序遍历左子树，然后访问根结点，再中序遍历右子树。如下图所示，中序遍历的顺序为GDHBAEICF。
【数据结构】二叉树的创建和四种遍历（附带详细注释）
在写二叉树的中序遍历结果时，有个更加快捷的方法：从树根向下将二叉树一脚踩扁，之后按照踩扁后的树，从左至右依次写出各结点的数据即可。以上图中的树为例，踩扁之后就变成了下图：
【数据结构】二叉树的创建和四种遍历（附带详细注释）
根据结点从左到右出现的次序，想象所有的结点都在一条线上，这样写出各结点的数据后得到的便是该树的中序遍历结果，即GDHBAEICF。

中序遍历递归算法

void in_order_traverse(TREE T)
{
   
	if (T) // T为空是递归结束的条件
	{
   
		in_order_traverse(T->leftchild);  // 中序遍历左子树
		putchar(T->data); // 打印根结点的数据
		in_order_traverse(T->rightchild); // 中序遍历右子树
	}
}

中序遍历非递归算法

中序遍历非递归算法用到了链栈的部分知识，，详细内容可以参见《链栈的实现》这篇文章。文章来源地址https://www.toymoban.com/news/detail-445621.html

链栈结构的设计

typedef TREE StackElemType; // 定义栈的元素类型为树结点的指针

// 定义栈的结点
typedef struct StackNode
{
   
	StackElemType data; // 数据域
	struct StackNode* next; // 指针域
}StackNode, * STACK; // STACK 等同于 struct StackNode *

// 定义链栈结构
typedef struct LinkedStack
{
   
	STACK top; // 栈顶指针
	int length; // 当前栈中元素的个数
}LinkedStack;

链栈操作函数的声明

void init_stack(LinkedStack&);
void push_stack(LinkedStack&, StackElemType);
bool stack_is_empty(LinkedStack&);
bool pop_stack(LinkedStack&, StackElemType&);
void destroy_stack(LinkedStack&);