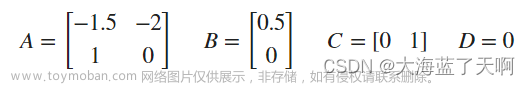矩阵理论| 基础：Jordan标准型（从Jordan标准型求代数重数/几何重数/特征向量）-Toy模板网

这篇具有很好参考价值的文章主要介绍了矩阵理论| 基础：Jordan标准型（从Jordan标准型求代数重数/几何重数/特征向量）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

引言：如何判定两个矩阵相似

相似矩阵，本质上是同一个线性变换在不同坐标系下的矩阵
因此，两个矩阵相似的一大特点是：特征值相同，各特征值的几何重数/代数重数相同

进而，我们可以用特征多项式、特征值、行列式、迹、秩等相似不变量来迅速辅助判定两个矩阵是否相似，但这些都不是充要条件

两个矩阵相似的充要条件：两个矩阵具有相同的Jordan标准型（包含了大量信息，如特征值、代数/几何重数、特征向量和可对角化判定的信息，下面会说明）

Jordan标准型是一整个“相似矩阵大家族”的典型代表，根据相似关系的传递性，上述结论显然

Jordan标准型

Jordan标准型可以视为一种“矩阵三角化”。（ps. 也可以理解为一种由Jordan块构成的主对角分块矩阵）

对于n阶方阵 $\mathbf A$ ，一定存在正交矩阵/酉矩阵 $\mathbf Q$ 使 $\mathbf A$ 相似于上三角阵： $\mathbf A=\mathbf Q\mathbf U\mathbf Q^T$ ，详见矩阵三角化的 Schur 定理
如果将正交矩阵改为普通的可逆矩阵 $\mathbf P$ ，同样可以得到上三角阵 $\mathbf J$ ，即Jordan标准型： $\mathbf A=\mathbf P\mathbf J\mathbf P^{-1}$

为何要三角化？Jordan标准型是由于无法相似对角化而提出的，而上三角阵就是最接近对角矩阵的“最佳形式”

Jordan标准型的一般形式

任何方阵 $\mathbf A$ 都相似于一个Jordan标准型: $\mathbf A=\mathbf P\mathbf J\mathbf P^{-1}$

Jordan标准型 $\mathbf J$ 由多个Jordan块组成
$\mathbf J=\left[\begin{array}{cccc} J_{m_1}\left(\lambda_{1}\right) & 0 & \cdots & 0 \\ 0 & J_{m_2}\left(\lambda_{2}\right) & \cdots & 0 \\ \vdots & \vdots & \ddots & \ddots \\ 0 & 0 & \cdots & J_{m_k}\left(\lambda_{k}\right) \end{array}\right]，其中J_{m_i}\left(\lambda_{i}\right)=\left[\begin{array}{cccc} \lambda_{i} & 1 & \\ & \ddots & \ddots & \\ & & \ddots & 1 \\ & & & \lambda_{i} \end{array}\right]_{m_i\times m_i}$
一般默认的排列顺序为 $\lambda_1\geq\lambda_2\geq...\geq\lambda_k$

每个Jordan块 $J\left(\lambda_{i}\right)$ 的对角线上为特征值 $\lambda_{i}$ ，对角线上方全为1

Jordan标准型中隐含的信息

特征值： $\mathbf J$ 的所有主对角元 $\lambda_1,...,\lambda_k$
特征值 $\lambda_i$ 的代数重数 $\beta_i$ ： $\mathbf J$ 的对角线上 $\lambda_i$ 的出现次数（特征值 $\lambda_i$ 的重根数）
ps. 代数重数满足 $\beta_i+\beta_2+...+\beta_k=n$
特征值 $\lambda_i$ 的几何重数 $n_i$ ：主对角元为 $\lambda_i$ 的Jordan块个数
（一个Jordan块对应一个独立的特征向量/一个几何重数）

矩阵可对角化，那么其所有特征值的几何重数=代数重数，也就是说其Jordan标准型中所有的Jordan块都必须为1阶的

或者说，可对角化矩阵，其Jordan标准型就是一个对角矩阵
某个Jordan块的特征向量（不是原矩阵 $\mathbf A$ 的特征向量）：

每个Jordan块可以被写为 $\begin{aligned}J_{m}(\lambda)&=\left[\begin{array}{cccc}\lambda & 1 & & \\& \ddots & \ddots & \\& & \ddots & 1 \\& & & \lambda\end{array}\right] \\ &=\left[\begin{array}{llll}\lambda & & & \\& \ddots & & \\& & \ddots & \\& & & \lambda\end{array}\right] +\left[\begin{array}{llll}0 & 1 & & \\& \ddots & \ddots & \\& & \ddots & 1 \\& & & 0\end{array}\right] \\ &=\lambda I_{m}+J_{m}(0)\end{aligned}$ 这是一个单位阵和一个幂零(nilpotent)矩阵
①单位阵的特征值为 $\lambda$ ，特征向量为任意向量（ $\lambda\bold I_{m}\bold x=\lambda\bold x$ ）
②幂零矩阵 $J_{m}(0)$ 的特征值为0，且相应的特征子空间维数为 $m - r ank = 1$ ，唯一的（单位长度）特征向量为 $\bold e_1$ （ $J_{m}(0)\bold e_1=\bold 0$ ），而对于其他标准单位向量则有 $J_{m}(0)\bold e_i=\bold e_{i-1},i>1$
由②，Jordan块的特征向量必然是标准单位向量（例如 $\bold e_i$ 代表单位阵 $\bold E$ 的第 $i$ 列）

综合①②可知，该Jordan块的特征向量为 $J_{m}(\lambda) \mathbf{e}_{1}=\lambda \mathbf{e}_{1} \\ J_{m}(\lambda) \mathbf{e}_{i}=\lambda \mathbf{e}_{i}+\mathbf{e}_{i-1}, \quad i=2, \ldots, m$

可以看出，每个 $m$ 阶的Jordan块 $J_{m}(0)$ 有且仅有一个特征向量 $\mathbf{e}_{1}$ （因此上面说“一个Jordan块对应一个几何重数”），而其余的 $m - 1$ 个标准单位向量 $\mathbf{e}_{2},\mathbf{e}_{3},...,\mathbf{e}_{m}$ 称为广义特征向量(generalized eigenvector)

（可对角化的矩阵，其无关特征向量可张成整个空间，而Jordan标准型的情况，其所有广义特征向量张成整个空间），详见Jordan 形式大解读（上） | 线代启示录

举例说明：

例如
$\begin{aligned}\mathbf J_{A} &=blkdiag(\left[\begin{array}{lll|l} 2 & 1 & 0 & 0 \\0 & 2 & 1 & 0 \\0 & 0 & 2 & 0 \\\hline 0 & 0 & 0 & 2\end{array}\right],\left[\begin{array}{ll}3 & 1 \\0 & 3\end{array}\right])\\ &=blkdiag(\left[\begin{array}{lll}2 & 1 & 0 \\0 & 2 & 1 \\0 & 0 & 2\end{array}\right], [2], \left[\begin{array}{ll}3 & 1 \\0 & 3\end{array}\right])\\ &=blkdiag(J_3(2),J_2(2),J_2(3))\end{aligned}和\begin{aligned}\mathbf J_{B}&=blkdiag(\left[\begin{array}{ll|ll} 2 & 1 & 0 & 0 \\0 & 2 & 0 & 0 \\\hline 0 & 0 & 2 & 1 \\0 & 0 & 0 & 2\end{array}\right] ,\left[\begin{array}{ll}3 & 1 \\0 & 3\end{array}\right]) \\ &=blkdiag(\left[\begin{array}{ll}2 & 1 \\0 & 2\end{array}\right], \left[\begin{array}{ll}2 & 1 \\0 & 2\end{array}\right], \left[\begin{array}{ll}3 & 1 \\0 & 3\end{array}\right])\\ &=blkdiag(J_2(2),J_2(2),J_2(3))\end{aligned}$
其中， $\mathbf J_{A}$ 的特征值为 $2, 3$ ：
特征值 $2$ 的代数重数为 $4$ ，几何重数为 $2$
特征值 $3$ 的代数重数为 $2$ ，几何重数为 $1$
$\mathbf J_{A}$ 的特征值 $2$ 的两个特征向量为 $\begin{aligned}{\left[\begin{array}{lll}2 & 1 & 0 \\0 & 2 & 1 \\0 & 0 & 2\end{array}\right]\rightarrow \mathbf{e}_{1}=(1,0,0,0,0,0)^{T}} \\ {[2] \rightarrow \mathbf{e}_{4}=(0,0,0,1,0,0)^{T}}\end{aligned}$ ；
$\mathbf J_{A}$ 的特征值 $3$ 的特征向量为 ${\left[\begin{array}{ll}3 & 1 \\0 & 3\end{array}\right] \rightarrow \mathbf{e}_{5}=(0,0,0,0,1,0)^{T}}$

$\mathbf J_{B}$ 的特征值为 $2, 3$ ：
特征值 $2$ 的代数重数为 $4$ ，几何重数为 $2$
特征值 $3$ 的代数重数为 $2$ ，几何重数为 $1$
$\mathbf J_{B}$ 的特征值 $2$ 的两个特征向量为 $\begin{aligned}{\left[\begin{array}{ll}2 & 1 \\0 & 2\end{array}\right] \rightarrow \mathbf{e}_{1}=(1,0,0,0,0,0)^{T}} \\ {\left[\begin{array}{ll}2 & 1 \\0 & 2\end{array}\right] \rightarrow \mathbf{e}_{3}=(0,0,1,0,0,0)^{T}}\end{aligned}$ ；
$\mathbf J_{B}$ 的特征值 $3$ 的特征向量为 ${\left[\begin{array}{ll}3 & 1 \\0 & 3\end{array}\right] \rightarrow \mathbf{e}_{5}=(0,0,0,0,1,0)^{T}}$