对于激活函数(Activation Function),存在两个问题:
- 为什么要用激活函数?
- 如何选择用哪种激活函数?
- 如何使用激活函数?
本博文将围绕这两个问题,首先介绍激活函数的作用,从而解决为什么要用激活函数这个问题;然后将依此展开四个常用激活函数,分析各自使用条件,从而解决如何选择这个问题。
为什么要用激活函数
激活函数是神经网络中的重要组成部分,因为它们为每个神经元的输出引入非线性。没有激活函数,神经网络将仅仅是一个线性回归模型,这将限制其学习数据中复杂的模式和关系的能力。
e
.
g
.
e.g.
e.g.
举例来看,我们引入一个最简单的神经网络,包含一个隐藏层以及一个输出层,隐藏层中只包括一个神经元:

若不使用激活函数,即:
g
(
z
)
=
z
g(z)=z
g(z)=z
替代使用激活函数的:(使用
s
i
g
m
o
i
d
sigmoid
sigmoid 举例)
g
(
z
)
=
s
i
g
m
o
i
d
(
z
)
z
=
w
⃗
⋅
x
⃗
+
b
g(z)=sigmoid(z)\\ z = \vec{w}·\vec{x} + b
g(z)=sigmoid(z)z=w⋅x+b
在隐藏层,有:
a
[
1
]
=
g
(
w
1
[
1
]
⋅
x
⃗
+
b
1
[
1
]
)
=
w
1
[
1
]
⋅
x
⃗
+
b
1
[
1
]
a^{[1]} = g(w_1^{[1]}·\vec{x}+b_1^{[1]}) = w_1^{[1]}·\vec{x}+b_1^{[1]}
a[1]=g(w1[1]⋅x+b1[1])=w1[1]⋅x+b1[1]
在输出层,有:
a
[
2
]
=
g
(
w
1
[
2
]
⋅
a
[
1
]
+
b
1
[
2
]
)
=
w
1
[
2
]
⋅
a
[
1
]
+
b
1
[
2
]
a^{[2]} = g(w_1^{[2]}·a^{[1]} + b_1^{[2]}) = w_1^{[2]}·a^{[1]} + b_1^{[2]}
a[2]=g(w1[2]⋅a[1]+b1[2])=w1[2]⋅a[1]+b1[2]
输出层可以化简为:
a
[
2
]
=
w
1
[
2
]
⋅
(
w
1
[
1
]
⋅
z
+
b
1
[
1
]
)
+
b
1
[
2
]
=
w
1
[
2
]
w
1
[
1
]
⋅
z
+
w
1
[
2
]
b
1
[
1
]
+
b
1
[
2
]
a^{[2]} = w_1^{[2]}·(w_1^{[1]}·z+b_1^{[1]}) + b_1^{[2]} = w_1^{[2]}w_1^{[1]}·z+ w_1^{[2]}b_1^{[1]} + b_1^{[2]}
a[2]=w1[2]⋅(w1[1]⋅z+b1[1])+b1[2]=w1[2]w1[1]⋅z+w1[2]b1[1]+b1[2]
即:
a
[
2
]
=
w
1
[
2
]
w
1
[
1
]
⋅
z
+
w
1
[
2
]
b
1
[
1
]
+
b
1
[
2
]
=
w
⋅
x
+
b
a^{[2]} = w_1^{[2]}w_1^{[1]}·z+ w_1^{[2]}b_1^{[1]} + b_1^{[2]} = w·x + b
a[2]=w1[2]w1[1]⋅z+w1[2]b1[1]+b1[2]=w⋅x+b
其中: w = w 1 [ 2 ] ⋅ w 1 [ 1 ] w = w_1^{[2]}·w_1^{[1]} w=w1[2]⋅w1[1], b = w 1 [ 2 ] ⋅ b 1 [ 1 ] + b 1 [ 2 ] b = w_1^{[2]}·b_1^{[1]} + b_1^{[2]} b=w1[2]⋅b1[1]+b1[2]
综上
综上所述,如果我们不使用激活函数,每个神经元输出的都是线性结果,神经网络仅仅是一个线性回归模型。而我们往往解决的问题存在两种形式:线性问题以及分类问题。
隐藏层与输出层
激活函数的选择会根据 输出层 和 隐藏层 的不同而有所不同。
隐藏层的主要作用是引入非线性
-
在神经网络的隐藏层中,激活函数的主要作用是引入 非线性,从而使神经网络能够学习更复杂的特征。
当神经网络只包含线性层时,无论有多少层,其整体仍然是线性的。这是因为线性层的输出是输入的线性组合,无法拟合非线性的函数。通过使用 非线性的激活函数,神经网络可以学习到更复杂的特征和模式,从而提高其表达能力和性能。 -
而复杂的特征需要 梯度下降 来学习,优化神经网络的参数。
梯度下降算法的核心思想是根据损失函数对参数进行梯度计算,并按照梯度的反方向对参数进行更新 – back propergation,从而逐步优化神经网络的参数,使得神经网络的预测结果更加准确。
当神经网络的特征更加复杂时,需要更多的参数来描述和学习这些特征。这就需要神经网络在参数空间中搜索更复杂的模型,以更好地拟合训练数据,并且能够泛化到新数据。通过梯度下降算法,神经网络可以在参数空间中搜索最优解,使得神经网络能够学习到更复杂的特征,从而提高其预测性能。
因此,更复杂的特征需要梯度下降来学习。在深度学习中,使用非线性的激活函数可以使神经网络具有更强的表达能力,从而学习到更复杂的特征,而使用梯度下降算法可以在参数空间中搜索最优解,进一步提高神经网络的性能。
说白了,就是隐藏层需要非线性,所以引入激活函数,而激活函数需要根据梯度下降来调整参数,而相比而言,Sigmoid, Softmax 更容易比 ReLU 梯度爆炸或者梯度消失,所以常用 ReLU;
输出层的主要作用是输出结果
- 输出层使用激活函数的目的就是为了输出结果;
- 输出层的激活函数取决于所解决的问题类型:
- 分类问题:多类别的分类问题用 softmax 函数作为输出层的激活函数;二分类问题通常使用 sigmoid 函数作为输出层的激活函数。
- 回归问题:回归问题使用线性激活函数或者 sigmoid 函数作为输出层的激活函数;
- 无激活函数:比如 GAN 生成对抗网络,后期阐述
四大激活函数
我们有四种常用的激活函数(Linear,Sigmoid,ReLU,Softmax),其中前三种更为广为人知;

-
Sigmoid 函数:Sigmoid 函数将任何实数映射到 (0, 1) 的区间内,常用于输出层的二分类问题。它的缺点是在大于 2 或小于 -2 的区间内,梯度接近于 0,导致梯度消失问题。
-
Linear 函数:linear 激活函数是一种非常简单的激活函数,也称为恒等激活函数。它的定义非常简单,即将神经元的输出等同于输入,linear 激活函数不具有非线性特性,因此通常仅用于回归问题的输出层。
-
ReLU 函数:ReLU 函数是一种常用的激活函数,它将负数映射为 0,将正数保留不变。ReLU 函数简单易实现,可以有效避免梯度消失问题,但是在神经元输出为负数时,梯度为 0,导致神经元无法更新。
Linear Activation Function
应用于: 回归问题的输出层。神经元的输出直接等同于模型的输出,无需进行非线性转换。神经元的输入为: z z z, z = w ⃗ ⋅ x ⃗ + b z = \vec{w}·\vec{x} + b z=w⋅x+b,输出同样为: z z z
公式为:
g
(
z
)
=
z
g(z) = z
g(z)=z
图像为:
Sigmoid Activation Function
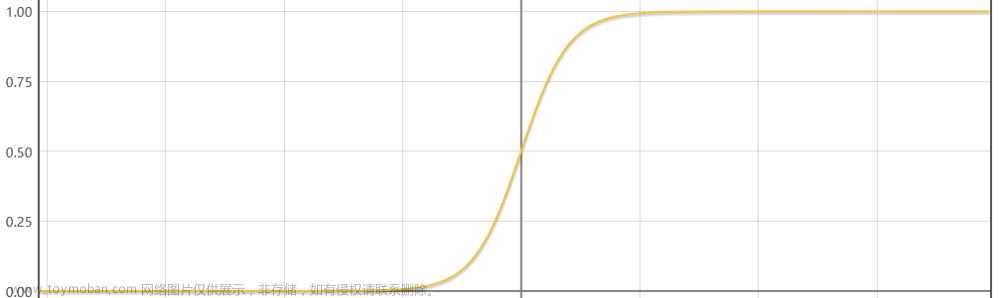
应用于: 分类问题输出层。Sigmoid 函数将任何实数映射到 (0, 1) 的区间内,常用于输出层的二分类问题。它的缺点是在大于 2 或小于 -2 的区间内,梯度接近于 0,导致梯度消失问题。
公式为:
g
(
z
)
=
1
1
+
e
−
z
g(z) = \frac {1} {1+e^{-z}}
g(z)=1+e−z1
图像为:
ReLU Activation Function
应用于: 分类问题输出层。ReLU 函数是一种常用的激活函数,它将负数映射为 0,将正数保留不变。ReLU 函数简单易实现,相比于 sigmoid,可以有效避免梯度消失问题,但是在神经元输出为负数时,梯度为 0,导致神经元无法更新。
公式为:
g
(
z
)
=
m
a
x
(
0
,
z
)
g(z) = max(0,z)
g(z)=max(0,z)
图像为:
Softmax Activation Function
应用于: 输出层的激活函数,以将网络的输出归一化为概率分布,以便进行多类别分类;正所谓多类别分类使用 softmax,二分类问题使用 sigmoid 函数;
公式为:
a
j
=
e
z
j
∑
k
=
1
N
e
z
k
a_j = \frac{e^{z_j}} {\sum_{k=1} ^N e^{z_k}}
aj=∑k=1Nezkezj
分析:
使用 Softmax 作为输出层的激活函数,有:
a 1 [ 3 ] = e z 1 [ 3 ] ∑ i = 1 N e z i [ 3 ] = P ( y = 1 ∣ x ⃗ ) a 2 [ 3 ] = e z 2 [ 3 ] ∑ i = 1 N e z i [ 3 ] = P ( y = 2 ∣ x ⃗ ) . . . a N [ 3 ] = e z N [ 3 ] ∑ i = 1 N e z i [ 3 ] = P ( y = N ∣ x ⃗ ) a_1^{[3]} = \frac {e^{z_1^{[3]}}} {\sum _{i=1} ^{N}e^{z_{i}^{[3]}}} = P(y=1|\vec{x}) \\ a_2^{[3]} = \frac {e^{z_2^{[3]}}} {\sum _{i=1} ^{N}e^{z_{i}^{[3]}}} = P(y=2|\vec{x}) \\ ... a_N^{[3]} = \frac {e^{z_N^{[3]}}} {\sum _{i=1} ^{N}e^{z_{i}^{[3]}}} = P(y=N|\vec{x}) a1[3]=∑i=1Nezi[3]ez1[3]=P(y=1∣x)a2[3]=∑i=1Nezi[3]ez2[3]=P(y=2∣x)...aN[3]=∑i=1Nezi[3]ezN[3]=P(y=N∣x)
正如上述公式所述;
同样,softmax 激活函数的损失函数为交叉熵损失函数,用来度量预测概率分布和真是概率分布之间的差异。在多分类问题中,softmax 函数将神经网络的输出转化为各个类别的概率分布,而交叉熵损失函数则是用于衡量神经网络的预测值和实际值之间的差异。
在二分类中,交叉熵损失函数为:
L
o
s
s
=
−
y
∗
l
o
g
a
1
−
(
1
−
y
)
∗
l
o
g
(
1
−
a
1
)
Loss = -y * log a_1 - (1-y) * log(1-a_1)
Loss=−y∗loga1−(1−y)∗log(1−a1)
而在多分类的 softmax 中,交叉熵损失函数为:
L
o
s
s
(
a
⃗
,
y
)
=
{
−
l
o
g
(
a
1
)
,
if
y
=
1
.
⋮
−
l
o
g
(
a
N
)
,
if
y
=
N
\begin{equation} Loss(\vec{a},y)=\begin{cases} -log(a_1), & \text{if $y=1$}.\\ &\vdots\\ -log(a_N), & \text{if $y=N$} \end{cases} \tag{3} \end{equation}
Loss(a,y)=⎩
⎨
⎧−log(a1),−log(aN),if y=1.⋮if y=N(3)
使用场景举例
下一篇博文将举例一个实际使用场景来进行多分类,本篇博文只做简单介绍:
model = Sequential(
[
Dense(25, activation = 'relu'),
Dense(15, activation = 'relu'),
Dense(4, activation = 'softmax')
]
)
model.compile(
loss=tf.keras.losses.SparseCategoricalCrossentropy(),
optimizer=tf.keras.optimizers.Adam(0.001),
)
model.fit(
X_train,y_train,
epochs=10
)
模型的创建
model = Sequential(
[
Dense(25, activation = 'relu'),
Dense(15, activation = 'relu'),
Dense(4, activation = 'softmax')
]
)
创建的模型为:两个隐藏层,一个输出层;
其中第一个隐藏层包含25个神经元,第二个隐藏层包含15个神经元,使用的激活函数为 ReLU激活函数;
输出层包含4个类别的输出,使用softmax激活函数;

配置模型的学习过程
在 tensorflow 中,通过 model.compile 配置模型的学习过程,下述代码,我们通过 loss 指定损失函数,通过 optimizer 指定优化器;
model.compile(
loss=tf.keras.losses.SparseCategoricalCrossentropy(),
optimizer=tf.keras.optimizers.Adam(0.001),
)
损失函数 loss
用于训练模型,使得模型准确率最高,常见的多类别损失函数包含: SparseCategoricalCrossentropy 与 CategoricalCrossentropy;
SparseCategoricalCrossentropy 与 CategoricalCrossentropy
两者皆是常用的多分类问题的损失函数,两者之间的区别在于标签 Label 的形式不同:
具体来说,就是:
SparseCategoricalCrossentropy:标签形式为整数索引;
CategoricalCrossentropy:标签形式为独热编码形式;
整数索引与独热编码形式
所谓 整数索引,就是整数索引,例如如果有10个潜在目标值,则 y 将介于 0~9 之间;
所谓 独热编码(One-hot Encoding) 形式,假设有三个类别:猫、狗、鸟,则独热编码为:
- 猫:[1, 0, 0]
- 狗:[0, 1, 0]
- 鸟:[0, 0, 1]
如此,我们将类别转化为一个固定长度的向量,方便计算机的存储和处理。但是很明显,如果分类的类别数量非常大时,独热编码格式会产生大量的维度,导致存储和计算成本非常高,因此可以采用稀疏矩阵的方法;若无需考虑计算距离问题,则可以使用类别的整数索引来替代独热编码,如此更加高效的处理多分类问题。
综上所属,如此看来,如果我们处理类别数量很大的多分类问题时,我们通常采用 SparseCategoricalCrossentropy 而非 CategoricalCrossentropy 损失函数方法;
优化器 optimizer
用于指定模型的优化算法,常见优化器包含:SGD,Adam,Adagrad等;不同的优化器适用于不同的场景和问题,选择合适的优化器可以提高模型的训练效率以及准确度;
随机梯度下降 SGD
每次迭代只随机选取一个样本进行梯度下降,更新模型参数。由于每次只更新一个样本参数,所以SGD的速度较快,但是会带来较大的噪声,导致训练不稳定;
批量梯度下降 BGD
BGD会将所有的样本全部参与到参数的更新中,每次迭代更新一次参数,与SGD相反的是,速度会比较慢,但是可以较好的控制训练过程中的噪声,而且需要耗费大量的内存空间;
小批量梯度下降 Mini-Batch SGD
SGD与BGD的折中办法,每次迭代会更新一部分参数,所以具备两个优化器的优点,即速度不错,噪声可控;
Adagrad
Adagrad是一种自适应的学习率优化算法,根据每个参数的历史梯度值来自适应的调整学习率,训练过程中逐渐降低学习率,使得模型在接近极值时更加稳定;
RMSProp
RMSProp是一种自适应的学习率优化算法,通过平均历史梯度值来自适应的调整学习率,有效控制训练过程中的噪声,防止参数震荡或者过拟合;
Adam(常用)
Adam是一种自适应的学习率,结合了Adagrad 与 RMSProp的优点,Adam每次迭代自适应地调整学习率,可以有效地控制训练速度以及稳定性;而我们使用地Adam优化器中的参数代表学习率 α = 0.001 \alpha = 0.001 α=0.001
模型的训练
model.fit(
X_train,y_train,
epochs=10
)
对模型进行训练,X_train 为输入数据,y_train 为标签,epochs 为训练的轮数。
附加:Softmax Python实现
a
j
=
e
z
j
∑
k
=
0
N
−
1
e
z
k
a_j = \frac{e^{z_j}}{ \sum_{k=0}^{N-1}{e^{z_k} }}
aj=∑k=0N−1ezkezj
def my_softmax(z):
a = np.zeros(len(z))
sums = 0.0
for i in range(len(z)):
sums += np.exp(z[i])
for i in range(len(z)):
a[i] = np.exp(z[i])/sums
return a
下一篇博文将围绕一个简单案例展开~文章来源:https://www.toymoban.com/news/detail-446226.html
2023.4.14文章来源地址https://www.toymoban.com/news/detail-446226.html
到了这里,关于【机器学习】P16 激活函数 Activation Function的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!