R统计绘图-多元线性回归(最优子集法特征筛选及模型构建，leaps)

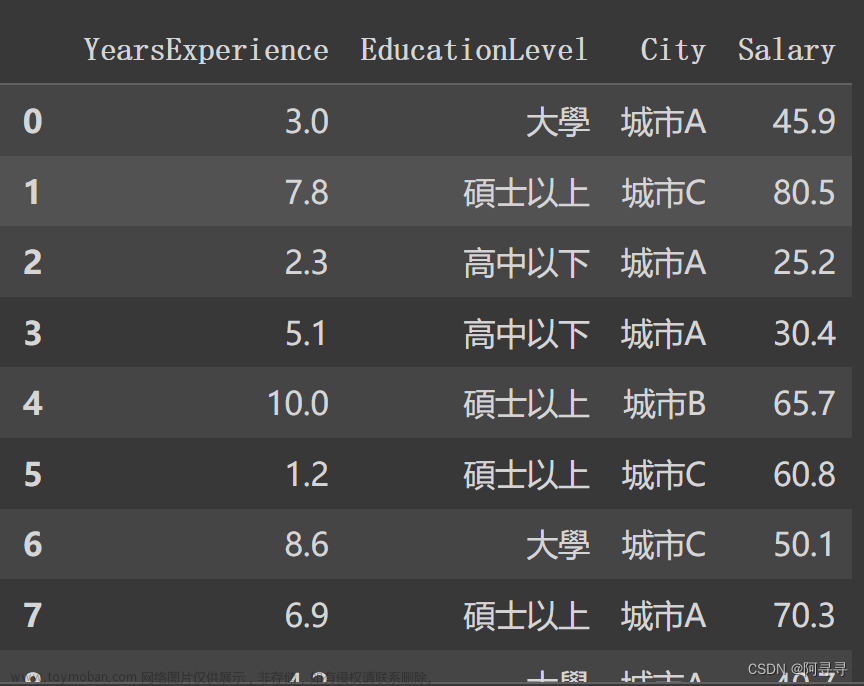
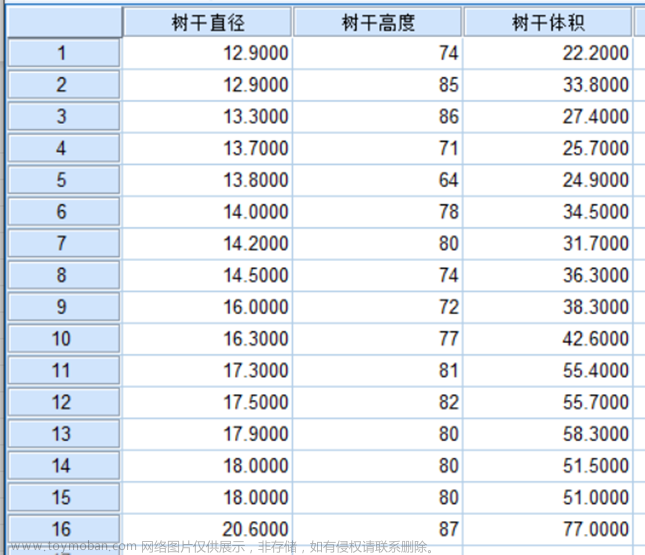
此文为《精通机器学习：基于R》的学习笔记，书中第二章详细介绍了线性回归分析过程和结果解读。

回归分析的一般步骤：

1. 确定回归方程中的自变量与因变量。

2. 确定回归模型，建立回归方程。

3. 对回归方程进行各种检验。

4. 利用回归方程进行预测。

此文介绍了如何使用leaps包进行最优子集特征筛选，然后基于筛选的特征进行模型构建及检验。

一、 数据准备及探索

实际上，有时只使用某种统计分析方法，或只看统计分析的统计量，而不看使用该统计方法的前提，或不进行数据探索，最后得到的分析结果可能与实际有偏差。因此，进行统计分析前，最重要的是要进行数据探索和假设检验，以此来选择适合自己数据的统计方法。如线性回归对分析的数据(自变量和因变量)就是有假设的。要进行线性线性回归必须满足一下假设：

1. 正态性：自变量和因变量呈正态分布。2. 独立性：每一个观测值随机误差都与其他观测值的随机误差相互独立，也就是任意一个观测值与其他所有的观测值没有任何关系，不论是在组内还是组间。应该是实验设计中就明确的事情。3. 线性：自变量与因变量之间存在线性相关，如果两者的线性关系不明显，根据数据探索结果，可以对变量进行对数、多项式或指数转换以解决问题。4. 同方差性：因变量的方差不会随着自变量的变化而变化；即，误差(真实值与预测值之间的差异)是正态分布的，并具有相同的方差，5. 自变量不存在多重共线性，即自变量不应该存在相关性。6. 不存在异常值，异常值会严重影响参数估计。

# 设置工作路径
#knitr::opts_knit$set(root.dir="D:\\EnvStat\\EcoEvoPhylo\\MLR")# 使用Rmarkdown进行程序运行
Sys.setlocale('LC_ALL','C') # Rmarkdown全局设置
#options(stringsAsFactors=F)# R中环境变量设置，防止字符型变量转换为因子

# 1.1 导入数据
library(tidyverse)
da <- read.csv("data.csv",row.names = 1)
da %>%
  head()

da.scale <- da %>%
  mutate(across(.cols = !contains(c("condition","depth","grazing")),.fns = scale), # 对数值数据进行标准化
         grazing = factor(grazing, levels = c("CK","LG","MG","HG")) # 将因子变量设置为实验设计顺序。
         #若要将分类变量用作线性回归分析，一定要进行此设置，将对照组排在第一位，分析时其会作为哑变量，即，它在回归方程中的回归系数会为0。
         ) %>% 
  #summarise_if(is.numeric,scale) %>% # 对数值数据进行标准化,且不保留分类变量
  data.frame()
da.scale %>%
  head()
  

图1|环境因子及分组信息表，data.csv。行为样品名称，列为环境因子名称和分组信息，共有11个环境变量，3个分组信息。

# 1.2 变量正态分布检验
## 1.2.1 多变量正态分布检验
library(rstatix)
mshapiro_test(da.scale[-c(1:3)])

## 1.2.2 单变量正态分布检验
assign("m",names(da.scale[-c(1:3)])) # 将变量名称，赋于m
m
da.scale %>% shapiro_test(m) # 对名称包括在m中的的环境因子进行shapiro test
##正态性检验未通过，如果数据不是严重偏态，线性回归结果仍然稳健。

图2|变量正态分布检验。正态性检验未通过，如果数据不是严重偏态，线性回归结果仍然稳健。

# 1.3 探索数据相关性
## 1.3.1 计算线性相关系数
library(psych)
da.cor <- psych::corr.test(da.scale[-c(1:3)], 
                           adjust="holm", 
                           alpha=.05,
                           ci=FALSE)$r %>%
  data.frame()
da.cor # 相关系数统计量，不一定能真实的反应数据情况。
##非线性相关变量，使用pearson相关系数会低估两者的相关性。

## 1.3.2 绘图探索变量两两间关系
#pairs(~ ., data = da.scale[-c(1:3)]) # base函数
library(GGally)
library(ggplot2)
p1 <- ggpairs(da,columns = 4:14, # 选择需要绘图的变量所在列号
        upper = list(continuous = "cor", 
                     na ="na"),
        lower = list(continuous = "smooth",
                     na ="na"),
        diag = list(continuous = "densityDiag",
                    na = "naDiag"))+
  theme_bw() 

pdf("p1.pdf",height = 15,width = 15,family = "Times")
print(p1)
dev.off()

图3|变量相关性分析。

自变量间存在显著的线性相关关系(例，AP vs. TN)，会存在多重共线性的问题，两个变量的相关性系数大于0.5，就应该考虑不要耐入同一个模型。对相关变量使用PCA等方法进行降维后，可以使用降维后变量作为解释变量构建模型。也可后续筛选变量的时候去除。根据自己需要筛选特征(自变量)。统计分析时，不能只看着统计量，最重要的是要进行数据探索和假设检验。

二、 模型构建

在进行多重线性回归时，自变量(特征)选择是一个十分重要的过程，直接影响模型的质量。常用的特征筛选的方法有：

1.前向逐步选择：从一个零模型开始，然后每次添加一个特征，直到所有特征添加完毕。在这个过程中，被添加的选定特征建立的模型具有最小的RSS。所以理论上，第一个选定的特征应该能最好的解释响应变量，依次类推。添加一个特征一定会使RSS减少，使R方增加，但不一定能提高模型的拟合度和可解释性。

2.后向逐步回归：从一个包含所有特征的模型开始，每次删除一个起最小作用的特征。现在也存在一种混合方法，这种算法先通过前向逐步回归添加特征，然后检查是否有特征不再对提高模型拟合度起作用，如果有则删除。值得注意的是，一个数据使用前向逐步选择和后向逐步选择，可能会得到两个完全矛盾的模型。最重要的是，逐步回归会使回归系数发生偏离，即，会使回归系数的值过大，置信区间过窄。

3.最优子集回归：算法使用所有可能的特征组合来拟合模型。分析者需要应用自己的判断和统计分析来选择最优模型。当特征数多于观测数时，这个方法的效果就不会好。此处介绍如何使用leaps包进行最优子集回归，筛选特征，用于构建模型。

2.1 最优子集特征选择-leaps包

library(leaps)
# 2.1.1 使用所有特征构建多元线性模型-全模型
fit1 <- lm(pH ~ .,data=da.scale[-1]) # 此处只是作为示例选择了pH作为因变量，没有生物学意义。
fit1 %>%
  summary() # 输出结果包括回归方程系数，线性关系检验、回归系数检验以及R方。

# 2.1.2 最优子集法进行特征选择
sub.fit <- regsubsets(pH ~ ., data = da.scale[-1])
sub.fit %>%
  summary()

best_summary <- summary(sub.fit)
names(best_summary) # 查看列表数据中包含的对象
which.min(best_summary$rss) # 具有8个特征的模型具有最小的rss。which.min和which.max()可用于筛选数据。
which.max(best_summary$adjr2)

# 2.1.3 使用赤池信息量准则，马洛斯的Cp，贝叶斯信息量准则和修正R方四种方法进行特征选择
## leaps不输出AIC值，但AIC与Cp成正比。
pdf("model_select.pdf",width=unit(7.5,"cm"),height=unit(10,"cm"))
par(mfrow=c(3,2), oma = c(0,0,0,0))
plot(best_summary$adjr2,ylab = "adjr2" ,xlab = "number of features")
plot(sub.fit,scale = "adjr2")

plot(best_summary$cp,ylab = "cp" ,xlab = "number of features")
plot(sub.fit,scale = "Cp")

plot(best_summary$bic,ylab = "bic" ,xlab = "number of features")
plot(sub.fit,scale = "bic")
dev.off()

图4|最优子集特征筛选。使用adjr2、Cp与BIC进行特征筛选。左侧图为模型中特征数量对应的特征筛选参数值。右侧图为特征筛选参数值对应包含的特征。

由图可知，当自变量为8个时，校正R方最大，对应变量是：grazingLG、grazingMG、grazingHG、depth20-30cm、AP、AK、OM、OC。当自变量为8个时，Cp最小，对应变量是：grazingLG、grazingMG、grazingHG、depth20-30cm、AP、AK、OM、OC。当自变量为4个时，BIC最小，对应变量是：grazingLG、grazingMG、depth20-30cm、AP。BIC和校正R方选择的最佳模型可能有区别，BIC倾向于选择变量较少的模型。这里使用校正R方选择特征。

2.2 构建模型并进行假设检验

如果想要保留尽量多的自变量，可根据校正R方和Cp值选择模型。选择grazing、depth、AP、AK、OM和OC，用以构建模型并进行模型检验。

# 2.2.1 构建模型
best_fit <- lm(pH ~ grazing + depth + AP + AK + OM + OC,
               data = da.scale)
# 此处没有考虑自变量的交互效应。实验设计要考虑两个变量的交互效应可使用AP:AK，所有交互效应则可使用*连接自变量。

best_fit %>%
  summary()

图5|最优模型检验。输出结果中Estimate， Std. Error， t value, Pr(>|t|):依次表示对应自变量的回归系数及其标准误，回归系数检验的t检验统计量及其p值。F-statistic: 2.421 on 2 and 15 DF, p-value: 0.1227 则是是对整个模型的显著性检验。分类因子作为自变量时，因子中的每个分类水平都会有一个回归系数，第一个分类水平作为哑变量，其回归系数为0。此模型中grazingCK和depth0-10cm的回归系数为0。

模型回归系数解释：以变量AP为例，其回归系数(偏回归系数)是-0.5810，表示在控制其它自变量不变的情况下，AP每增加一个单位，因变量pH平均减少0.5810个单位。分类变量的解释稍有不同，以grazingLG为例，grazingLG的偏回归系数1.1080表示grazingLG的pH平均比grazingCK的pH高1.1080个单位。自变量若单位不统一，方差比较大的自变量，就可能支配目标函数，使模型不能像预期的那样正确的从其它特性中学习，所以分析前需要对数据进行缩放。

## 回归参数的置信区间
confint(best_fit) 

## 提取效应值
effects(best_fit) 

## 提取残差
residuals(best_fit)

## 提取回归系数
coefficients(best_fit)

## 计算模型AIC值
AIC(best_fit)

## 模型预测
predict(best_fit) # 将新的观测值代入，可以预测对应的新因变量。进行区间[构建模型因变量范围]内预测比较准。

# 2.2.2 anova查看方差分析表
anova(best_fit) # 输出模型中自变量是否具有统计学意义。

图6|方差分析表。结果包括自由度，离均差平方，均方误差，F检验值(=均方误差除以残差)和p值

三、 线性回归必须满足的假设检验

3.1 生成模型拟合诊断图进行初步检验

library(car)
par(mfrow = c(2,2))
plot(best_fit)

图7|模型拟合诊断图。

模型拟合诊断图解释：

1. 正态性：当自变量值固定时，因变量成正态分布，则残差值也应该是一个均值为0的正态分布。正态Q-Q(分位数-分位数)图(Normal Q-Q，右上)是在正态分布对应的值下，标准化残差的概率图。若满足正态假设，那么图上的点应该落在呈45度角的直线上；若不是如此，那么就违反了正态性的假设。Q-Q图表示一个变量的分位数对应于另一个变量的分位数画出的图，从图中也可以看到离群点。
2. 线性： 若因变量与自变量线性相关，那么残差值与预测(拟合)值就没有任何系统关联。换句话说，除了噪声(随机误差)，模型应该包含数据中所有的系统方差。如果在“残差图与拟合图”(Residuals vs Fitted，左上)中看到一个曲线关系，表示可能需要对回归模型加上一个二次项。
3. 同方差性： 若满足不变方差假设，那么在位置尺度图(Scale-Location Graph，左下)中，水平线周围的点应该随机分布。该图似乎满足此假设。误差的异方差性通常会表现为U形曲线或反U形曲线，也可能会紧密聚集在图的左侧，随着拟合值的增加逐渐变宽(漏斗形)。
4. 异常值：残差杠杆图(Residuals vs Leverage，右下)可以用以确定那个观测值会对模型造成过度影响。从图形可以鉴别出离群点、高杠杆值点和强影响点。下面来详细介绍：

4.1 离群点：表明拟合回归模型对其预测效果不佳(产生了巨大的或正或负的残差)。

4.2 高杠杆值点：表明它是一个异常的自变量值的组合。也就是说，在自变量空间中，它是一 个离群点。因变量值不参与计算一个观测点的杠杆值。

4.3 强影响点(influential observation)：表明它对模型参数的估计产生的影响过大，非常不成比例。强影响点可以通过Cook距离(Cook’s D)统计量来鉴别。如果Cook距离的值大于1，则需要进行更深入的检查。在样本足够的情况下，可以删除异常点，强影响点。不删除样本的话，可以对数据进行对数、指数或多项式转换，以消除影响。

3.2 自变量与因变量满足线性关系

构建完模型后，应该对其残差进行探索，看残差中还存在何种模式。若图形存在非线性，则说明可能对自变量的函数形式建模不够充分，那么就需要添加一些曲线成分，比如多项式项，或对一个或多个变量进行变换(如用log(X)代替X)，或用其他回归模型而不是线性回归。

# 成分残差图，car包。删除有NA数的解释变量再进行。
crPlots(best_fit, one.page = TRUE, ask = FALSE)

图8|成分残差图。

3.3 同方差性检验

误差是正态分布,且成同方差性。如果违背了这个假设，参数估计就有可能产生偏差，导致对显著性的统计检验借故偶过高或过低，从而得出错误结论，称为异方差。

# 3.3.1 Q-Q图确定残差是否符合正态性
## 对于不同变量残差的方差是一个固定值。
car::qqPlot(best_fit) # 绘制带置信区间的Q-Q图。

图9| Q-Q图。如果拒绝了误差正态分布，那么就该考虑进行变量转换和删除观测值。图中标注出的落在置信区间外的观测点可以认为是离群点。

## 3.3.2 Breusch-Pagan检验误差的同质性
library(lmtest)
bptest(best_fit) # p>0.05,接受零假设，满足误差的同质性。

# 3.3.3 计分检验-判断误差方差是否恒定
ncvTest(best_fit) # p>0.05,接受零假设，满足误差的同质性。

图10| 同方差检验。p>0.05,接受零假设，满足误差的同质性。

# 3.3.4 分布水平图-展示标准化残差绝对值与拟合值
spreadLevelPlot(best_fit)

图11| 分布水平图。图中展示了展示标准化残差绝对值与拟合值。图中的点在水平的最佳拟合曲线周围呈水平随机分布。若违反了该假设，图中将会是一个非水平的曲线。代码结果建议幂次变换(suggested power transformation)的含义是，经过p次幂变换，非恒定的误差方差将会平稳。例如，若图形显示出了非水平趋势，建议幂次转换为0.5，在回归等式中用自变量的0.5次幂代替自变量，可能会使模型满足同方差性。若建议幂次为0，则使用对数变换。对于当前例子，异方差性很不明显，因此建议幂次接近1，则不需要进行变换。

3.4 自变量共线性研究-方差膨胀因子检验

研究自变量线性问题，常用方差膨胀因子(Variance Inflation Factor，VIF)这一统计量，VIF是一个比率，分子为使用全部特征拟合模型时该特征的系数的方差，分母为仅使用该特征拟合模型时这个特征的系数的方差。VIF的平方根表示变量回归参数的置信区间能膨胀为与模型无关的预测变量的程度。car包中的vif()函数提供VIF值。VIF能取的最小值是1，表示根本不存在共线性。现在还没有一个确定的统计学标准来决定多重共线性什么时候会使模型变的不可接受。一般认为VIF值大于5或10就说明存在严重的共线性。解决共线性的简单方式是，在不影响预测能力的情况下去掉这个变量。

# 3.4.1 计算VIF
## 特征之间不应该存在相关性，共线性也会导致估计偏差。
car::vif(best_fit) # OM和OC的VIF>10,可以删除这两个变量，然后重新构建模型。5或10是VIF较常用的阈值。
##此步骤也可放在特征筛选前面，先对全模型的自变量计算方差膨胀因子
car::vif(fit1) # 一定要在把有严重相关性变量去除后，再进行这一步，模型中共线性严重，运行此函数可能会报错。
##任何函数使用都需要满足一定的规则，遇到报错，根据报错信息查看错误原因，善用网络搜索。
##模型构建工作根据自己需要调整。

图12|计算VIF值。在全模型时，即可计算VIF值，然后去除VIF值高的自变量。有时候保存高VIF值变量，并不影响模型预测精度。特征变量的筛选可以根据自己的实际需要进行。

# 3.4.2 去除高VIF自变量，重新拟合模型
best_fit2 <- lm(pH ~ grazing+depth+AP+AK,da.scale)
best_fit2 %>%
  summary() # 校正R方值只有轻微降低。

图13|重构模型统计结果。删除高VIF值自变量后，R方只有轻微降低。

3.5 异常值检验

一个全面的回归分析要覆盖对异常值的分析，包括离群点、高杠杆值点和强影响点。异常值会严重影响参数估计，可能对结果产生较大的负面影响。

# 3.5.1 离群点
## Q-Q图中落在置信区间带外的点即可被认为是离群点。
## 另外一个粗糙的判断准则：标准化残差值大于2或3或者小于-2或-3的点可能是离群点。
## 在使用线性回归拟合模型之前最好除去异常值。
outlierTest(best_fit) # p<0.05,存在离群点。

图14|离群点检验结果。p<0.05,存在离群点。该函数只是根据单个最大(或正或负)残差值的显著性来判断是否有离群点。若不显著，则说明数据集中没有离群点；若显著，则必须删除该离群点，然后再检验是否还有其他离群点存在。

# 3.5.2 高杠杆值点
## 高杠杆值观测点，即是与其他预测变量有关的离群点。
##换句话说，它们是由许多异常的预测变量值组合起来的，与响应变量值没有关系。
hat.plot <- function(fit){
    p <- length(coefficients(fit))
    n <- length(fitted(fit))
    plot(hatvalues(fit), main = "Index Plot of Hat Values")
    abline(h = c(2, 3) * p/n, col = "red", lty = 2)
    identify(1:n, hatvalues(fit), names(hatvalues(fit)))
}
hat.plot(best_fit) # 不存在高杠杆点

图15|高杠杆值点。高杠杆值的观测点可通过帽子统计量(hat statistic)判断。对于一个给定的数据集，帽子均值为p/n，其中p是模型估计的参数数目(包含截距项)，n是样本量。一般来说，若观测点的帽子值大于帽子均值的2或3倍，即可以认定为高杠杆值点。帽子值反应了一个特定的观测值在模型中有多大的影响力。高杠杆值点可能会是强影响点，也可能不是，这要看它们是否是离群点。代码来自《R语言实战》第八章。

# 3.5.3 强影响点
## 强影响点是指对模型参数估计值影响有些比例失衡的点。
##例如，若移除模型的一个观测点时模型会发生巨大的改变，那么就需要检测一下数据中是否存在强影响点了。
## 有两种方法可以检测强影响点：Cook距离，或称D统计量，以及变量添加图(added variableplot)。
##一般来说，Cook’s D值大于4/(n-k -1)，则表明它是强影响点，其中n为样本数量，k是自变量回归系数数目(不包含截距项)。
##也经常以D=1为分割点来判断该观测点是否是强影响点。
## 绘制Cook's D图
##identify D values > 4/(n-k-1)
cutoff <- 4/(nrow(da.scale) - length(best_fit$coefficients) - 2)
plot(best_fit, which = 4, cook.levels = cutoff)
abline(h = cutoff, lty = 2, col = "red") # 若删除LGC3与MGA2点，将会导致回归模型截距项和斜率发生显著变化，两个是强影响点。

图16|Cook's D图。若删除LGC3与MGA2点，将会导致回归模型截距项和斜率发生显著变化，两个是强影响点。也经常用D=1为分割点来判断该观测点是否是强影响点。代码来自《R语言实战》第八章。

## 绘制变量添加图
##相对于Cook’s D图有助于鉴别强影响点，变量添加图还可以提供关于这些点如何影响模型的信息。
##对于一个响应变量和k个预测变量，可以创建k个变量添加图。
##变量添加图，即对于每个预测变量Xk，绘制Xk在其他k-1个预测变量上回归的残差值相对于响应变量在其他k-1个预测变量上回归的残差值的关系图。
## car包中的avPlots()函数可绘制供变量添加图。
avPlots(best_fit, ask = FALSE, onepage = TRUE, id.method = "identify")

图17|变量添加图。图中的直线表示相应预测变量的实际回归系数。图中强影响点带有标注，可以想象删除某些强影响点后直线的改变，以此来估计它的影响效果。

# 3.5.4 离群点、高杠杆值和强影响点的信息整合
##利用car包中的influencePlot()函数，可以将离群点、高杠杆值和强影响点的信息整合到一幅图中。
influencePlot(best_fit, id.method = "identify", main = "Influence Plot", 
    sub = "Circle size is proportial to Cook's Distance")

图18|离群点、高杠杆值和强影响点的信息整合图。图中纵坐标超过+2或小于-2的观测点可被认为是离群点，横坐标超过0.2或0.3的观测点有高杠杆值(通常为预测值的组合)。圆圈大小与影响成比例，圆圈很大的点可能是对模型参数的估计造成的不成比例影响的强影响点。没有通过检验的点将会在图后列出。

3.6 误差的独立性-判断隐变量值(或残差)是否相互独立

误差的独立性没有很好的方法进行检验，通常根据经验确定。durbinWatsonTest()可以检验时序数据的误差独立性检验。

#durbinWatsonTest(best_fit) # p值不显著(p=0.326)说明无自相关性，误差项之间独立。
## 此函数用于时序数据检验

注：更多输出结果见MLR1.html文件。

3.7 拟合值与真实值绘图查看模型预测效果

da.scale["Actual"] <- da.scale$pH
da.scale$Forecast <- predict(best_fit)
library(ggplot2)
ggplot(da.scale,
       aes(x = Forecast,y = Actual)
         )+
  geom_point()+
  geom_smooth(method = "lm")+
  labs(title = "Forecast vs. Actual")

图19|模型预测效果图。

3.8 线性模型假设的综合验证

gvlma包中的gvlma()函数能对线性模型假设进行综合验证，同时还能做偏斜度、峰度和异方差性的评价。换句话说，它给模型假设提供了一个单独的综合检验(通过/不通过)。

library(gvlma)
gvmodel <- gvlma(best_fit)
summary(gvmodel)

图20|线性模型假设的综合验证。从Global Stat中可以看到数据满足线性回归模型所有的统计假设(p=0.4815)。若Decision下的文字表明违反了假设条件(比如p<0.05)，则可使用前述方法依次判断哪些假设没有被满足。

数据不满足多重线性回归的假设，根据具体未通过的假设，可以采取1)删除观测点；2)变量变换；3)添加或删除变量；4)使用其他回归方法等改进措施。

四、 概念解释

4.1 相关分析与回归分析

相关分析是研究两个或两个以上变量之间相关(线性或非线性)程度及大小的一种统计方法。计算得到的相关性系数只是表示变量间相关性的强弱，不代表具体的数学关系，没有单位。回归分析是寻找存在相关关系(线性或非线性)的变量间的数学表达式，并进行统计推断的一种统计方法。计算得到的回归系数能用于表达变量间的明确数学关系，具有单位。

4.2 误差(Error)、离差(Deviation)与残差(Residual)

误差是模型的一个总体参数，是模型中的误差项，描述的是因变量被随机因素导致的变化，即真实值和预测值之间存在的差异。误差是独立并且具有相同的分布，并且服从均值为0方差为θ^2的正态分布。

残差则是针对因变量真实值与模型拟合值之差，是误差的一个抽样。

离差则是因变量与因变量均值的差，总离差可分解为残差与拟合值两部分。

数据及代码可以QQ交流群文件夹中下载，或公众号后台发送“MLR1”获取。

原文链接：R统计绘图-多重线性回归(最优子集法特征筛选，leaps) (qq.com)

参考资料

[误差、离差与残差](https://blog.csdn.net/qq_43382509/article/details/105179378)

《R语言实战》

统计学：从数据到结论 4d[吴喜之]

《精通机器学习：基于R》

Borcard, Daniel, François Gillet and Pierre Legendre. Numerical Ecology with R. Use R! Cham: Springer International Publishing, 2018. https://doi.org/10.1007/978-3-319-71404-2.

R绘图-物种、环境因子相关性网络图(简单图、提取子图、修改图布局参数、物种-环境因子分别成环径向网络图)

R统计绘图-分子生态相关性网络分析(拓扑属性计算，ggraph绘图)

R统计绘图-变量分组相关性网络图(igraph)

机器学习-分类随机森林分析(randomForest模型构建、参数调优、特征变量筛选、模型评估和基础理论等)

R统计绘图 | 物种组成堆叠柱形图(绝对/相对丰度)

R统计绘图 | 物种组成冲积图(绝对/相对丰度，ggalluvial)

R统计绘图 | 物种组成桑基图(不同分类单元微生物丰度及其从属关系，ggalluvial) -免费送书

R统计绘图 | 物种组成堆叠面积图(绝对/相对丰度，ggalluvial)

R统计绘图 | 物种组成气泡图和聚类热图(ggplot2/ComplexHeatmap)

R统计绘图-随机森林分类分析及物种丰度差异检验组合图

机器学习-多元分类/回归决策树模型(tree包)

R统计绘图-环境因子相关性+mantel检验组合图(linkET包介绍1)

R统计绘图-NMDS、环境因子拟合(线性和非线性)、多元统计(adonis2和ANOSIM)及绘图(双因素自定义图例)

R统计绘图-RDA分析、Mantel检验及绘图

R绘图-RDA排序分析R统计绘图-VPA(方差分解分析)

R统计绘图-PCA详解1(princomp/principal/rcomp/rda等)

R统计-PCA/PCoA/db-RDA/NMDS/CA/CCA/DCA等排序分析教程

R统计绘图-PCA分析绘图及结果解读(误差线，多边形，双Y轴图、球形检验、KMO和变量筛选等)

R统计-微生物群落结构差异分析及结果解读

R统计绘图-PCA分析及绘制双坐标轴双序图R统计绘图-分子生态相关性网络分析

R中进行单因素方差分析并绘图R统计-多变量单因素参数、非参数检验及多重比较

R绘图-相关性分析及绘图

R绘图-相关性系数图

R统计绘图-环境因子相关性热图

R统计绘图-corrplot绘制热图及颜色、字体等细节修改

R统计绘图-corrplot热图绘制细节调整2(更改变量可视化顺序、非相关性热图绘制、添加矩形框等)

R数据可视化之美-节点链接图

R统计绘图-rgbif包下载GBIF数据及绘制分布图

R统计-单因素ANOVA/Kruskal-Wallis置换检验

R统计-正态性分布检验[Translation]

R统计-数据正态分布转换[Translation]

R统计-方差齐性检验[Translation]

R统计-Mauchly球形检验[Translation]

R统计绘图-单、双、三因素重复测量方差分析[Translation]

R统计绘图-混合方差分析[Translation]

R统计绘图-协方差分析[Translation]

R统计绘图-One-Way MANOVA

文献管理 | Endnote使用小技巧(修改引文格式、合并文献库、删除重复文献和更新文献信息等)

Alignment--本地blast使用详解1-数据库序列检索下载及比对文章来源地址https://www.toymoban.com/news/detail-446323.html

到了这里，关于R统计绘图-多元线性回归(最优子集法特征筛选及模型构建，leaps)的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！