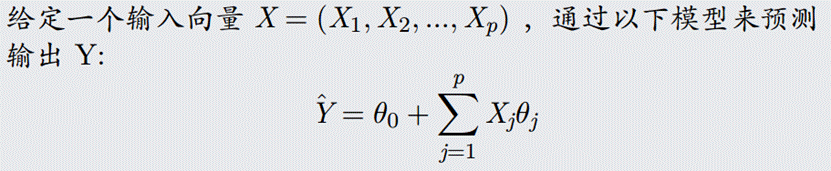线性回归基本介绍
线性回归: w 1 ∗ x 1 + w 2 ∗ x 2 + w 3 ∗ x 3 + . . . + w n ∗ x n + b i a s w_1 * x_1 + w_2 * x_2 + w_3 * x_3 + ...+ w_n * x_n + bias w1∗x1+w2∗x2+w3∗x3+...+wn∗xn+bias
1:准备好1特征1目标值(都为100行1列)
y = x ∗ 0.7 + 0.8 y = x * 0.7 + 0.8 y=x∗0.7+0.8
2: 建立模型 随机初始化准备一个权重w,一个向量b
y p r e d i c t = x ∗ w + b y_{predict} = x * w + b ypredict=x∗w+b
3:求损失函数,误差
loss 均方误差: ( y 1 − y 1 ′ ) 2 + ( y 2 − y 2 ′ ) 2 + ( y 3 − y 3 ′ ) 2 + . . . + ( y 100 − y 100 ′ ) 2 (y_1-y_1^{'})^2 + (y_2-y_2^{'})^2 + (y_3-y_3^{'})^2 + ... + (y_{100}-y_{100}^{'})^2 (y1−y1′)2+(y2−y2′)2+(y3−y3′)2+...+(y100−y100′)2
4:梯度下降优化
矩阵相乘:
(m行,n行) * (n行,1)(m行,1)
常用的op
矩阵运算:
tf.matmul(x,w)
平方:
tf.square(error)
均值:
tf.reduce_mean(error)
梯度下降优化:
tf.train.GradientDescentOptimizer(learning_rate)
- learning_rate:学习率
- method:
minize(loss)
- return:梯度下降op
自实现线性回归预测
import tensorflow as tf
# 1.准备数据 x:特征值 [100,1] y 目标值[100]
x = tf.random_normal([100,1], mean = 1.75, stddev = 0.5,name = "x_data")
# 矩阵相乘必须是二维的
y_ture = tf.matmul(x,[[0.7]]) + 0.8
# 2.建立线性回归模型,1个特征,1个权重,一个偏置 y = xw + b
# 随机给一个权重和p偏置的值,计算损失,然后在当前状态下优化
# 用变量定义才能优化
weight = tf.Variable(tf.random_normal([1,1],mean = 0.0,stddev = 1.0),name = "w")
bias = tf.Variable(0.0,name = "b")
y_predict = tf.matmul(x,weight) + bias
# 3.建立损失函数,均方误差
loss = tf.reduce_mean(tf.square(y_ture - y_predict))
# 4.梯度下降优化损失 leaning_rate:0.01,0.03,0.1,0.3,......
train_op = tf.train.GradientDescentOptimizer(0.1).minimize(loss)
# 定义一个初始化变量的op
init_op = tf.global_variables_initializer()
# 通过会话运行程序
with tf.Session() as sess:
# 初始化变量
sess.run(init_op)
# 打印随机最先初始化的权重和偏置
print("随机初始化的参数权重为:%f, 偏置为:%f" %(weight.eval(),bias.eval()))
# 循环运行优化
for i in range(200):
sess.run(train_op)
print("第%d次优化的参数权重为:%f, 偏置为:%f" % (i,weight.eval(),bias.eval()))
随机初始化的参数权重为:-1.260226, 偏置为:0.000000
第0次优化的参数权重为:0.349570, 偏置为:0.856385
第1次优化的参数权重为:0.554503, 偏置为:0.966013
第2次优化的参数权重为:0.590992, 偏置为:0.982879
第3次优化的参数权重为:0.600176, 偏置为:0.984269
第4次优化的参数权重为:0.602949, 偏置为:0.982530
第5次优化的参数权重为:0.603653, 偏置为:0.980223
第6次优化的参数权重为:0.602477, 偏置为:0.976848
第7次优化的参数权重为:0.604590, 偏置为:0.975368
......
第193次优化的参数权重为:0.689427, 偏置为:0.819917
第194次优化的参数权重为:0.689293, 偏置为:0.819553
第195次优化的参数权重为:0.689415, 偏置为:0.819265
第196次优化的参数权重为:0.689980, 偏置为:0.819289
第197次优化的参数权重为:0.690093, 偏置为:0.819089
第198次优化的参数权重为:0.689954, 偏置为:0.818728
第199次优化的参数权重为:0.689771, 偏置为:0.818355
tensorflow 变量作用域
tf.variable_scope(<scope_name>):创建指定名字的变量作用域
import tensorflow as tf
with tf.variable_scope("data"):
x = tf.random_normal([100,1], mean = 1.75, stddev = 0.5,name = "x_data")
# 矩阵相乘必须保持数据是二维的
y_ture = tf.matmul(x,[[0.7]]) + 0.8
with tf.variable_scope("model"):
# 随机给一个权重和p偏置的值,计算损失,然后在当前状态下优化
# 用变量定义才能优化
# trainable参数:指定这个变量能顺着梯度下降一起优化
weight = tf.Variable(tf.random_normal([1,1],mean = 0.0,stddev = 1.0),name = "w")
bias = tf.Variable(0.0,name = "b")
y_predict = tf.matmul(x,weight) + bias
with tf.variable_scope("loss"):
# 3.建立损失函数,均方误差
loss = tf.reduce_mean(tf.square(y_ture - y_predict))
with tf.variable_scope("optimizer"):
# 4.梯度下降优化损失 leaning_rate:0.01,0.03,0.1,0.3,......
train_op = tf.train.GradientDescentOptimizer(0.1).minimize(loss)
# 定义一个初始化变量的op
init_op = tf.global_variables_initializer()
# 通过会话运行程序
with tf.Session() as sess:
# 初始化变量
sess.run(init_op)
# 打印随机最先初始化的权重和偏置
print("随机初始化的参数权重为:%f, 偏置为:%f" %(weight.eval(),bias.eval()))
# 把图结构写入事件文件
filewriter = tf.summary.FileWriter("./tmp/summary/test2",graph = sess.graph)
# 循环运行优化
for i in range(200):
sess.run(train_op)
print("第%d次优化的参数权重为:%f, 偏置为:%f" % (i,weight.eval(),bias.eval()))
随机初始化的参数权重为:-0.364948, 偏置为:0.000000
第0次优化的参数权重为:0.660532, 偏置为:0.544167
第1次优化的参数权重为:0.773921, 偏置为:0.608918
第2次优化的参数权重为:0.791829, 偏置为:0.620703
第3次优化的参数权重为:0.793604, 偏置为:0.624149
第4次优化的参数权重为:0.788609, 偏置为:0.624627
第5次优化的参数权重为:0.791536, 偏置为:0.627871
第6次优化的参数权重为:0.789608, 偏置为:0.629258
第7次优化的参数权重为:0.789247, 偏置为:0.631952
第8次优化的参数权重为:0.790944, 偏置为:0.635684
......
第194次优化的参数权重为:0.709682, 偏置为:0.782486
第195次优化的参数权重为:0.709192, 偏置为:0.782562
第196次优化的参数权重为:0.709601, 偏置为:0.783022
第197次优化的参数权重为:0.709102, 偏置为:0.782941
第198次优化的参数权重为:0.709275, 偏置为:0.783254
第199次优化的参数权重为:0.709096, 偏置为:0.783376
体现在tensorboard上:下图出现多个optimizer的原因可能是在notebook上运行时,如果重复执行原来的代码,变量名也会自动改变,默认了之前的模型是存在的。需要注意的是,在加载保存的模型时需要注意,重复运行包含op在内的代码会导致模型加载不出来,因为名称已变。

模型的保存和加载
-
tf.train.Saver(var_list = None,max_to_keep=5)
-
var_list:指定将要保存和还原的变量。它可以作为一个dict或一个列表传递
-
max_to_keep: 指示要保留的最近检查点文件的最大数量。创建新文件时,会删除较旧的文件。如果无或0,则保留所有检查点文件。默认为5,即保留最新的5个检查点文件。
-
-
例如: saver.save(sess,‘/temp/ckpt/test/model’)
saver.restore(sess,‘/temp/ckpt/test/model’) -
保存文件格式:checkpoint文件(检查点文件)
初次运行模型并保存
# 保存运行了500步的模型,下次直接从500步开始
import tensorflow as tf
with tf.variable_scope("data"):
x = tf.random_normal([100,1], mean = 1.75, stddev = 0.5,name = "x_data")
# 矩阵相乘必须保持数据是二维的
y_ture = tf.matmul(x,[[0.7]]) + 0.8
with tf.variable_scope("model"):
# 随机给一个权重和p偏置的值,计算损失,然后在当前状态下优化
# 用变量定义才能优化
# trainable参数:指定这个变量能顺着梯度下降一起优化
weight = tf.Variable(tf.random_normal([1,1],mean = 0.0,stddev = 1.0),name = "w")
bias = tf.Variable(0.0,name = "b")
y_predict = tf.matmul(x,weight) + bias
with tf.variable_scope("loss"):
# 3.建立损失函数,均方误差
loss = tf.reduce_mean(tf.square(y_ture - y_predict))
with tf.variable_scope("optimizer"):
# 4.梯度下降优化损失 leaning_rate:0.01,0.03,0.1,0.3,......
train_op = tf.train.GradientDescentOptimizer(0.1).minimize(loss)
# 收集tensor
tf.summary.scalar("losses",loss)
#tf.summary.scalar("weights1",weight) # weight一般是高维的要用histogram,但是由于这里是一维所以用scalar
tf.summary.histogram("weights2",weight) # 高维度的情况下一般用histogram
# 定义合并tensor的op
merged = tf.summary.merge_all()
# 定义一个初始化变量的op
init_op = tf.global_variables_initializer()
# 定义一个保存模型的实例
saver = tf.train.Saver()
# 通过会话运行程序
with tf.Session() as sess:
# 初始化变量
sess.run(init_op)
# 打印随机最先初始化的权重和偏置
print("随机初始化的参数权重为:%f, 偏置为:%f" %(weight.eval(),bias.eval()))
# 把图结构写入事件文件
filewriter = tf.summary.FileWriter("tmp/summary/test",graph = sess.graph)
# 循环运行优化
for i in range(500):
sess.run(train_op)
# 运行合并的tensor
summary = sess.run(merged)
filewriter.add_summary(summary,i)
print("第%d次优化的参数权重为:%f, 偏置为:%f" % (i,weight.eval(),bias.eval()))
saver.save(sess,"tmp/ckpt/model")
随机初始化的参数权重为:-0.265290, 偏置为:0.000000
第0次优化的参数权重为:0.668151, 偏置为:0.499340
第1次优化的参数权重为:0.796031, 偏置为:0.570753
第2次优化的参数权重为:0.813327, 偏置为:0.583293
第3次优化的参数权重为:0.811708, 偏置为:0.586319
第4次优化的参数权重为:0.809507, 偏置为:0.588334
第5次优化的参数权重为:0.811250, 偏置为:0.592284
第6次优化的参数权重为:0.813352, 偏置为:0.596134
。。。
第495次优化的参数权重为:0.700331, 偏置为:0.799402
第496次优化的参数权重为:0.700326, 偏置为:0.799410
第497次优化的参数权重为:0.700312, 偏置为:0.799412
第498次优化的参数权重为:0.700302, 偏置为:0.799414
第499次优化的参数权重为:0.700309, 偏置为:0.799429
直接加载模型再次运行,可以看到模型的权重和偏置是接着上次运行的结果进一步运行的
with tf.Session() as sess:
# 初始化变量
sess.run(init_op)
# 打印随机最先初始化的权重和偏置
print("随机初始化的参数权重为:%f, 偏置为:%f" %(weight.eval(),bias.eval()))
# 加载模型,覆盖模型当中随机定义的参数,从上次训练的参数结果开始
if os.path.exists("tmp/ckpt/checkpoint"):
saver.restore(sess,"tmp/ckpt/model")
# 循环运行优化
for i in range(500):
sess.run(train_op)
print("第%d次优化的参数权重为:%f, 偏置为:%f" % (i,weight.eval(),bias.eval()))
随机初始化的参数权重为:-1.206198, 偏置为:0.000000
INFO:tensorflow:Restoring parameters from tmp/ckpt/model
第0次优化的参数权重为:0.700308, 偏置为:0.799436
第1次优化的参数权重为:0.700309, 偏置为:0.799444
第2次优化的参数权重为:0.700299, 偏置为:0.799446
第3次优化的参数权重为:0.700287, 偏置为:0.799447
第4次优化的参数权重为:0.700289, 偏置为:0.799456
第5次优化的参数权重为:0.700291, 偏置为:0.799465
第6次优化的参数权重为:0.700283, 偏置为:0.799469
第7次优化的参数权重为:0.700294, 偏置为:0.799482
第8次优化的参数权重为:0.700279, 偏置为:0.799485
。。。
第491次优化的参数权重为:0.700001, 偏置为:0.799998
第492次优化的参数权重为:0.700001, 偏置为:0.799998
第493次优化的参数权重为:0.700001, 偏置为:0.799998
第494次优化的参数权重为:0.700001, 偏置为:0.799998
第495次优化的参数权重为:0.700001, 偏置为:0.799998
第496次优化的参数权重为:0.700001, 偏置为:0.799998
第497次优化的参数权重为:0.700001, 偏置为:0.799998
第498次优化的参数权重为:0.700001, 偏置为:0.799998
第499次优化的参数权重为:0.700001, 偏置为:0.799998
自定义命令行参数
1.tf.app.flags,它支持应用从命令行接受参数,可以用来指定集群配置等。在tf.app.flags下面有各种定义参数的类型
-
DEFINE_string(flag_name,default_value,docstring)
-
DEFINE_integer(flag_name,default_value,docstring)
-
DEFINE_boolean(flag_name,default_value,docstring)
-
DEFINE_float(flag_name,default_value,docstring)
2.tf.app.flags,在flags中有一个FLAGS标志,它在程序中可以调用到我们前边具体定义的flag_name
3.通过tf.app.run()启动main(argv)函数
模型训练
import tensorflow as tf
# 定义命令行参数
# 1、首先定义有哪些参数需要在运行的时候指定
# 2、程序当中获取定义命令行参数
# 第一个参数:名字,默认值,说明
tf.app.flags.DEFINE_integer("max_step",100,"模型训练的步数")
tf.app.flags.DIFINE_integer("model_dir"," ","模型文件的加载路径")
# 定义获取命令行参数名字
FLAGS = tf.app.flags.FLAGS
with tf.variable_scope("data"):
x = tf.random_normal([100,1], mean = 1.75, stddev = 0.5,name = "x_data")
# 矩阵相乘必须保持数据是二维的
y_ture = tf.matmul(x,[[0.7]]) + 0.8
with tf.variable_scope("model"):
# 随机给一个权重和p偏置的值,计算损失,然后在当前状态下优化
# 用变量定义才能优化
# trainable参数:指定这个变量能顺着梯度下降一起优化
weight = tf.Variable(tf.random_normal([1,1],mean = 0.0,stddev = 1.0),name = "w")
bias = tf.Variable(0.0,name = "b")
y_predict = tf.matmul(x,weight) + bias
with tf.variable_scope("loss"):
# 3.建立损失函数,均方误差
loss = tf.reduce_mean(tf.square(y_ture - y_predict))
with tf.variable_scope("optimizer"):
# 4.梯度下降优化损失 leaning_rate:0.01,0.03,0.1,0.3,......
train_op = tf.train.GradientDescentOptimizer(0.1).minimize(loss)
# 收集tensor
tf.summary.scalar("losses",loss)
#tf.summary.scalar("weights1",weight) # weight一般是高维的要用histogram,但是由于这里是一维所以用scalar
tf.summary.histogram("weights2",weight) # 高维度的情况下一般用histogram
# 定义合并tensor的op
merged = tf.summary.merge_all()
# 定义一个初始化变量的op
init_op = tf.global_variables_initializer()
# 定义一个保存模型的实例
saver = tf.train.Saver()
# 通过会话运行程序
with tf.Session() as sess:
# 初始化变量
sess.run(init_op)
# 打印随机最先初始化的权重和偏置
print("随机初始化的参数权重为:%f, 偏置为:%f" %(weight.eval(),bias.eval()))
# 把图结构写入事件文件
filewriter = tf.summary.FileWriter("tmp/summary/test",graph = sess.graph)
# 循环运行优化
for i in range(500):
sess.run(train_op)
# 运行合并的tensor
summary = sess.run(merged)
filewriter.add_summary(summary,i)
print("第%d次优化的参数权重为:%f, 偏置为:%f" % (i,weight.eval(),bias.eval()))
saver.save(sess,"tmp/ckpt/model")
模型调用文章来源:https://www.toymoban.com/news/detail-446547.html
with tf.Session() as sess:
# 初始化变量
sess.run(init_op)
# 打印随机最先初始化的权重和偏置
print("随机初始化的参数权重为:%f, 偏置为:%f" %(weight.eval(),bias.eval()))
# 加载模型,覆盖模型当中随机定义的参数,从上次训练的参数结果开始
if os.path.exists("tmp/ckpt/checkpoint"):
saver.restore(sess,FLAGS.model_dir)
# 循环运行优化
for i in range(FLAGS.max_step):
sess.run(train_op)
print("第%d次优化的参数权重为:%f, 偏置为:%f" % (i,weight.eval(),bias.eval()))
saver.save(sess,FLAGS.model_dir)
命令行代码:文章来源地址https://www.toymoban.com/news/detail-446547.html
python XXX.py --max_step=500 --model_dir="./tmp/ckpt/model"
到了这里,关于TensorFlow 1.x学习(系列二 :4):自实现线性回归的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!