二叉树的存储方式、遍历、构建、判定

目录

树的定义

二叉树的定义

二叉树的存储表示

二叉树的创建和前中后序遍历

通过中序遍历和先序遍历来构建树

通过后序遍历加先序遍历构建树

链式存储的树 将其中序遍历

非递归后序遍历

非递归后序遍历第二种方法

非递归中序遍历

非递归前序遍历

层次遍历

求二叉树节点个数

求二叉树深度

判断一个数是不是满二叉树

判断一个数是不是完全二叉树

树的定义

树是由n个结点组成的有限集合，如果 n=0 ，称为空树，如果n>0则

1、有一个特定的称之为根（root）的结点，它只有直接后继，但没有直接前驱；

2、除根以外的其他结点划分为m（m>=0）个互不交互的有限集合，每个集合又是一棵树，称为子树。每个子树的根节点只有一个直接前驱。

节点的度：一个节点含有的子树的个数

树的度：最大节点的度称为树的度

叶节点：度为零的节点

分支节点：度不为零

兄弟节点：含有相同父节点的节点

节点的层次：从根开始定义起，根为第一层，根的子节点为第二层

深度：对于任意节点n，n的深度为从根到n的唯一路径长，根的深度为0；

二叉树的定义

一棵二叉树是结点的一个有限集合，是由一个根节点加上两颗分别称为左子树和右子树的、互不相交的二叉树组成。

二叉树的性质：

每一个结点最多有两个子结点

高度为k的二叉树节点数最多为2的k+1次方-1

满二叉树：

每一层都达到了结点的最大个数

完全二叉树：

高度为h的树，共有h+1层，除h层以外，都达到最大个数，第h层从右向左连续缺若干结点，这就是完全二叉树。

二叉树的存储表示

顺序存储：当从0下标开始时，左孩子：i*2+1 右孩子：i*2+2 父节点：(i-1)/2 

假设只有右孩子 就会导致很多下标处没有数据 太浪费空间 所以存在第二种存储方式，一般只有完全二叉树才用数组存放

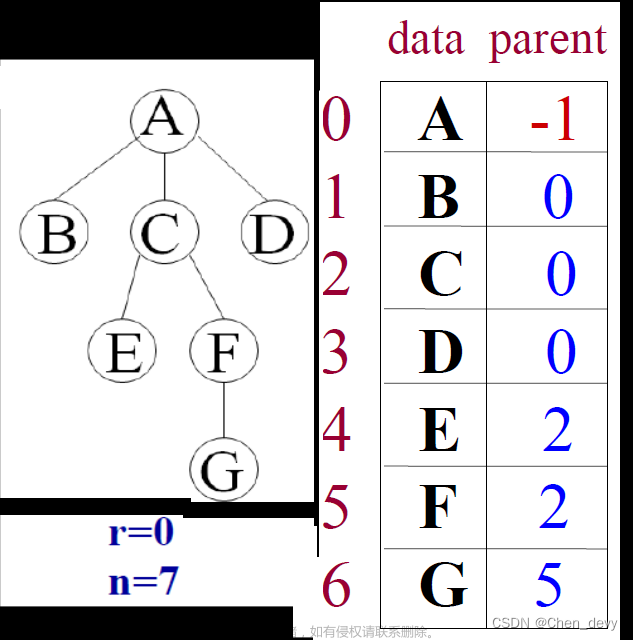
链式存储 ：分为二叉链表和三叉，区别是结构体里有没有parent指针 便于回溯文章来源地址https://www.toymoban.com/news/detail-446763.html

二叉树的创建和前中后序遍历

typedef char Elemtype;
typedef struct BtNode
{
	struct BtNode* leftchild;
	struct BtNode* rightchild;
	Elemtype data;
}BtNode,*BinartTree;

void InOrder(BtNode* ptr)//中序遍历
{
	if (ptr == NULL) { return; }
	InOrder(ptr->leftchild);
	cout << ptr->data << endl;
	InOrder(ptr->rightchild);
}
void PreOrder(BtNode* ptr)//先序遍历
{
	if (ptr == NULL) { return; }
	cout << ptr->data << endl;
	PreOrder(ptr->leftchild);
	PreOrder(ptr->rightchild);
}
void PastOrder(BtNode* ptr)//后序遍历
{
	if (ptr == NULL) { return; }
	PastOrder(ptr->leftchild);
	PastOrder(ptr->rightchild);
	cout << ptr->data << endl;
}
BtNode* BuyNode()
{
	BtNode* ptr = (BtNode*)malloc(sizeof(BtNode));
	if (ptr == nullptr)exit(1);
	memset(ptr, 0, sizeof(BtNode));
	return ptr;

}
BtNode* CreatTree(const char*& str)
{
	if (str == nullptr && strlen(str) <= 0) { return nullptr; }
	BtNode* s = nullptr;
	if (*str != '#') {
		s = BuyNode();
		s->data = *str;
		s->leftchild = CreatTree(++str);
		s->rightchild = CreatTree(++str);
	}
	return s;
}
int main()
{
	const char* str = "ABC##DE##F##G#H##";
	BinartTree  root = CreatTree(str);
	PastOrder(root);
	PreOrder(root);
	InOrder(root);
	return 0;
}

通过中序遍历和先序遍历来构建树

int Findpos(const char* ptr, int n, char first)
{
	int pos = -1;
	for (int i = 0; i < n; i++)
	{
		if (ptr[i] == first) { pos = i;  break; }
	}
	return pos;
}
BtNode* CreateBTreePI(const char* str, const char* ptr, int n)
{
	BtNode* s = nullptr;
	if (n > 0) 
	{
		s = BuyNode();
		s->data = str[0];
		int pos = Findpos(ptr, n, str[0]);
		if (pos == -1) { exit(1); }
		s->leftchild = CreateBTreePI(str+1, ptr, pos);
		s->rightchild = CreateBTreePI(str+pos+1, ptr+pos+1, n-pos-1);
	}
		return s;
}
BtNode* CreatBinartTreePI(const char* str, const char* ptr)
{
	int n = strlen(str);
	int m = strlen(ptr);
	if (nullptr == ptr || nullptr == str || n < 1 || m < 1 || n != m) { return nullptr; }
	else { return CreateBTreePI(str, ptr,n); }
}

int main()
{
	const char* str = "ABCDEFGH";
	const char* ptr = "CBEDFAGH";
	BinartTree  root = CreatBinartTreePI(str, ptr);
	return 0;
}

通过后序遍历加先序遍历构建树

int Findpos(const char* ptr, int n, char first)
{
	int pos = -1;
	for (int i = 0; i < n; i++)
	{
		if (ptr[i] == first) { pos = i;  break; }
	}
	return pos;
}
BtNode* CreateBTreePL(const char* ptr, const char* ltr, int n)
{
	BtNode* s = nullptr;
	if (n > 0)
	{
		s = BuyNode();
		s->data = ltr[n-1];
		int pos = Findpos(ptr, n, ltr[n-1]);
		if (pos == -1) { exit(1); }
		s->leftchild = CreateBTreePL(ptr, ltr, pos);
		s->rightchild = CreateBTreePL(ptr + pos+1 , ltr + pos, n - pos - 1);
	}
		return s;
}
BtNode* CreatBinartTreePL(const char* ptr, const char* ltr)
{
	int n = strlen(ptr);
	int m = strlen(ltr);
	if (nullptr == ptr || nullptr == ltr || n < 1 || m < 1 || n != m) { return nullptr; }
	else { return CreateBTreePL(ptr, ltr, n); }
}

int main()
{
	const char* str = "ABCDEFGH";
	const char* ptr = "CBEDFAGH";
	const char* ltr = "CEFDBHGA";
	BinartTree  root = CreatBinartTreePL(ptr, ltr);
	return 0;
}

链式存储的树 将其中序遍历

void InOrder_Ar(const int* ar, int n, int i)
{
	if (i < n) {
		InOrder_Ar(ar, n, i * 2 + 1);
		if (ar[i] != -1)
		{
			cout << ar[i] << " ";
		}
		InOrder_Ar(ar, n, i * 2 + 2);
	}
}
int main()
{
	int ar[] = { 31,23,12,66,-1,5,17,70,62,-1,-1,-1,88,-1,55 };
	int n = sizeof(ar) / sizeof(ar[0]);
	InOrder_Ar(ar, n, 0);


	return 0;
}

非递归后序遍历

if (nullptr == ptr) { return; }
	stack<BtNode*> st;
	BtNode* tag = nullptr;
	while (!st.empty() || ptr != nullptr) {
		while (ptr != nullptr)
		{
			st.push(ptr);
			ptr = ptr->leftchild;
		}
		ptr = st.top();
		st.pop();
		if (ptr->rightchild == nullptr || ptr->rightchild == tag)
		{
			cout << ptr->data << " ";
			tag = ptr;
			ptr = nullptr;
		}
		else
		{
			st.push(ptr);
			ptr = ptr->rightchild;
		}
	}

非递归后序遍历第二种方法

struct StkNode
{
	BtNode* Pnode;
	int popnum;
};

void NicePastOrder_2(BtNode* ptr)
{
	if (ptr == nullptr) { return; }
	stack<StkNode>st;
	st.push(StkNode{ ptr,0 });
	while (!st.empty())
	{
		StkNode node = st.top(); st.pop();
		if (++node.popnum == 3)
		{
			cout << node.Pnode->data << " ";
		}
		else
		{
			st.push(node);
			if (node.popnum == 1 &&node.Pnode->leftchild != nullptr)
			{
				st.push(StkNode{ node.Pnode->leftchild,0 });
			}
			else if(node.popnum == 2 &&node.Pnode->rightchild!=nullptr)
			{
				st.push(StkNode{ node.Pnode->rightchild,0 });
			}
		}
	}
	cout << endl;
}

非递归中序遍历

void NiceInOrder(BtNode* ptr)
{
	if (nullptr == ptr) {return;}
	stack<BtNode*> st;
	while (!st.empty() || ptr != nullptr) {
		while (ptr != nullptr)
		{
			st.push(ptr);
			ptr = ptr->leftchild;
		}
		ptr = st.top();
		st.pop();
		cout << ptr->data << " ";
		ptr = ptr->rightchild;
	}
}

非递归前序遍历

void NicePerOrder(BtNode* ptr)
{
	if (nullptr == ptr) { return; }
	stack<BtNode*>st;
	st.push(ptr);
	while (!st.empty())
	{
		ptr = st.top();
		st.pop();
		cout << ptr->data << " ";
		if (ptr->rightchild != nullptr)
		{
			st.push(ptr->rightchild);
		}
		if(ptr->leftchild!= nullptr)
		{
			st.push(ptr->leftchild);
		}
	}
	cout << endl;

}

层次遍历

void LevelOrder(BtNode* ptr)
{
	if (ptr == nullptr)return;
	queue<BtNode*> qu;
	qu.push(ptr);
	while (!qu.empty())
	{
		ptr = qu.front();
		qu.pop();
		cout << ptr->data << " ";
		if (ptr->leftchild != nullptr)
		{
			qu.push(ptr->leftchild);
		}
		if (ptr->rightchild != nullptr)
		{
			qu.push(ptr->rightchild);
		}
	}
	cout << endl;
}

求二叉树节点个数

int GetSize(BtNode *ptr)
{
	if (ptr == nullptr) {
		return 0;
	}
	return GetSize(ptr->leftchild) + GetSize(ptr->rightchild) + 1;
}

求二叉树深度

int Max(const int a, const int b)
{
	return a > b ? a : b;
}
int GetDepth(BtNode* ptr)
{
	if (ptr == nullptr) {
		return 0;
	}
	return Max(GetDepth(ptr->leftchild) , GetDepth(ptr->rightchild))+1;
}

判断一个数是不是满二叉树

bool IfFullBinartTree(BtNode* ptr)
{
	bool ret = true;
	if (ptr == nullptr)return ret;
	queue<BtNode*>qua;
	queue<BtNode*>qub;
	int i = 0;
	int n = 1;
	qua.push(ptr);
	while (!qua.empty() || !qub.empty())
	{
		for (; i < n && !qua.empty(); i++)
		{
			ptr = qua.front(); qua.pop();
			if (ptr->leftchild != nullptr)
			{
				qub.push(ptr->leftchild);
			}
			if (ptr->rightchild != nullptr)
			{
				qub.push(ptr->rightchild);
			}
		}
		if (i < n)
		{
			ret == false;
			break;
		}
		if (qub.empty())break;
		n += n;
		for (i = 0; i < n && !qub.empty(); i++)
		{
			ptr = qub.front(); qub.pop();
			if (ptr->leftchild != nullptr)
			{
				qua.push(ptr->leftchild);
			}
			if (ptr->rightchild != nullptr)
			{
				qua.push(ptr->rightchild);
			}
		}
		if (i < n)
		{
			ret = false;
			break;
		}
		if (qua.empty())break;
		n += n;
	}
	return ret;
}

判断一个数是不是完全二叉树

bool isfull(BtNode* ptr)
{
	bool ret = true;
	if (ptr != nullptr)return 0;
	queue<BtNode*>qu1;
	qu1.push(ptr);
	while (!qu1.empty())
	{
		ptr = qu1.front(); qu1.pop();
		if (ptr == nullptr)break;
		qu1.push(ptr->leftchild);
		qu1.push(ptr->rightchild);
	}
	while (!qu1.empty())
	{
		if (qu1.front() != nullptr) {
			ret = false;
			break;
		}
		qu1.pop();
	}
	return ret;
}

到了这里，关于二叉树的存储方式、遍历、构建、判定的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！