一、机器人介绍
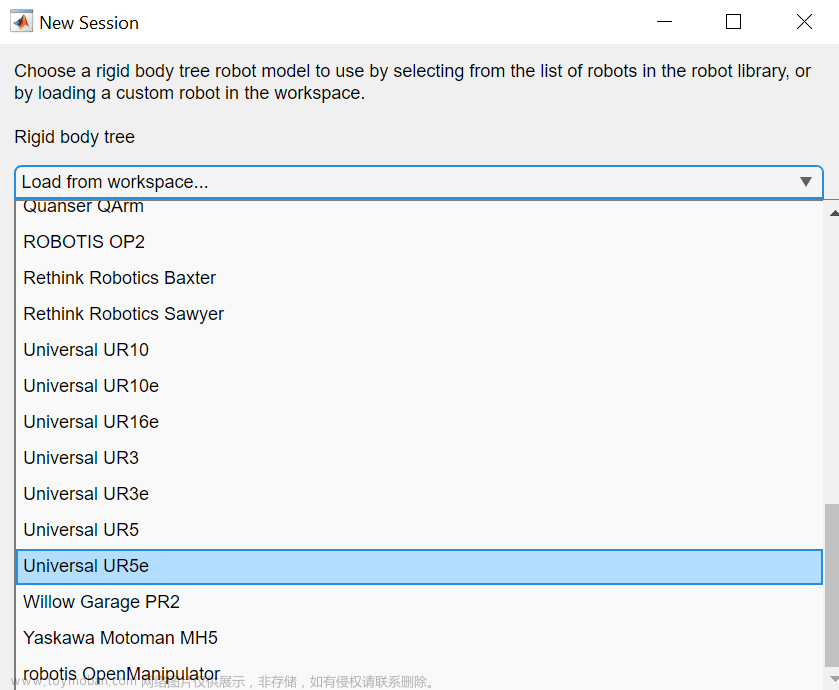
此处是基于MATLAB RVC工具箱,对ABB-IRB-1200型号的微型机械臂进行正逆向运动学分析,并利Simulink工具实现对机械臂进行具有动力学参数的末端轨迹规划仿真,最后根据机械模型设计Simulink-Adams联合仿真。

图1. ABB IRB 1200 尺寸参数示意图
ABB IRB 1200提供的两种型号广泛适用于各作业,且两者间零部件通用,两种型号的工作范围分别为700 mm 和 900 mm,大有效负载分别为 7 kg 和5 kg。 IRB 1200 能够在狭小空间内能发挥其工作范围与性能优势,具有全新的设计、小型化的体积、高效的性能、易于集成、便捷的接口、坚固耐用等的特点。全新设计:IRB 1200 的设计兼顾功能与美观。光洁的表面便于清洁和保养。IRB 1200 第2轴无外凸,使其具有比其他小型机器 人更长的行程,缩短了机器人与工件之间的距离。小型化的体积: IRB 1200机身小巧,有效工作范围宽大,有利于加快生产节拍,减少设备占用空间。 易于集成:IRB 1200 内置4 条气管、10 路用户信号线及以太网线,在设计上充分考虑了集成的便利性。坚固耐用:两种型号的 IRB 1200 均能以任意角度安装,标配IP 40防护等级, 可选IP 67防护等级。
二、机器人正向运动学分析
该机器人的旋转副定义如图2所示,包含6个旋转关节,机械臂末端具有x、y、z、rotx、roty rotz六个自由度,其中前三个是平移自由度,后三个是旋转自由度,通过对机械臂各个关节进行坐标系建立可以得到图3所示的坐标关系图。

图2. ABB-IRB-1200 关节示意图
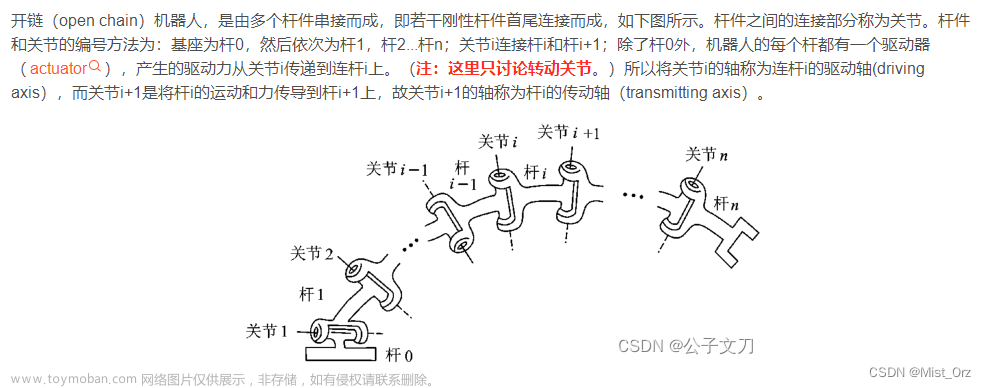
根据ABB1200机器人的关节布置,可以根据机器人学上的坐标选取原则选取机器人每个关节的坐标系,并根据关节连杆关系推导得出坐标之间的变换矩阵。机器人建模中的连杆坐标系的几个选取原则:(1)连杆n两端有关节n和n+1关节坐标系z轴的建立:旋转关节,按右手旋转的方向,变量为旋转角θ;(2)滑动关节,定义z轴为沿直线运动方向,变量为沿z轴的连杆长度d;(3)定义关节n的z轴编号为n-1;(4)关节不一定平行或相交(5)两关节的z轴(zn和zn+1)必有一条距离最短的公垂线an+1 xn+1方向为沿an+1方向(5)若两个关节z轴平行,则有无数条公垂线,选择与前一关节的公垂线共线的一条公垂线;(6)若两个关节z轴相交,则选择垂直于zn和zn+1构成的平面的直线作为x轴。结合ABB-IRB-1200 关节形式与尺寸可得机器人的坐标系c0到c6的示意图如下,其中θi为关节角度变量,z逆时针方向为正方向。其中,

图3. ABB-IRB-1200 机械臂坐标定义图示
所以每个坐标之间的传递矩阵可以表示为




通过代入符号变量运算可得正运动的表达式如图(不全,具体见附录),带入具体关节角度验证可得如下图, RVC工具箱DH建模得到的数值对比验证可得建模无误。


根据上述的DH矩阵参数,根据DH建模的选取原则设计如下的基于RVC程序。

程序反馈显示出的机器人DH参数。

RVC的可视化模型如图,可见,与ABB-IRB-1200 机械臂的实物图形完全对应一致。


三、机器人逆向运动学分析
根据机器人的正逆向运动学的求解方法,结合机器人解耦设计的准则:如果最后三个关节坐标相交于一点,可以将逆向运动学问题解耦成两个:逆向位置运动学Inverse position kinematics、 逆向方位运动学Inverse orientation kinematics,显然ABB-IRB-1200 机械臂满足该准则,可以利用数值解法或者几何+数值解法两种求解。本实验采用几何法+数值解法求解的方式,其中θ1-θ3利用几何法简便求得,θ4-θ6利用传递矩阵对应相等求解线性方程组的方式求得。















方法一:求解器求解。

方法二:几何法+解释法解算。



通过MATLABRVC的逆运动学解求解器对正运动学求解得到的传递矩阵,可以得到逆运动学解的角度值如下。

证明逆运动学解的求解运算正确。经验证,代入其他角度得到的结果也是对应一致的,值得注意的是,机器人由于存在奇异解,利用公式编程求解得出的偶尔会出现不对应情况,RVC工具箱逆运动学解求解器则一直是对应一致的。分析原因:可能因为在几何法求解的时候没有做好位型的选取,但是求解器中是通过解方程组数值解的方式,一旦位置于姿态信息确定,而且机械臂是解耦型控制,正反解的结果严格对应。
四、机械臂动力学模型
根据该型号机械臂的尺寸、质量、重心、关节摩擦、电机摩擦、粘度、减速比等参数计算出仿真中用到的动力学参数可以建立起该机械臂的动力学模型,通过动力学计算公式便可计算出相关的广义力,扭矩等控制量,也可以做机械臂的运动负载分析,可为控制设计提供参考。
4.1 参数介绍
L(1) = Revolute('d', 0, ... % link length (Dennavit-Hartenberg notation)
'a', 0, ... % link offset (Dennavit-Hartenberg notation)
'alpha', pi/2, ... % link twist (Dennavit-Hartenberg notation)
'I', [0, 0.35, 0, 0, 0, 0], ... % inertia tensor of link with respect to center of mass I = [L_xx, L_yy, L_zz, L_xy, L_yz, L_xz]
'r', [0, 0, 0], ... % distance of ith origin to center of mass [x,y,z] in link reference frame
'm', 0, ... % mass of link
'Jm', 200e-6, ... % actuator inertia
'G', -62.6111, ... % gear ratio
'B', 1.48e-3, ... % actuator viscous friction coefficient (measured at the motor)
'Tc', [0.395 -0.435], ... % actuator Coulomb friction coefficient for direction [-,+] (measured at the motor)
'qlim', [-160 160]*deg ); % minimum and maximum joint angle
4.2 动力学模型
du=pi/180;
L1=Revolute('d',0.399,'a',0,'alpha',pi/2,...
'I',[0,0.67,0,0,0,0],...
'r',[0,0,0],...
'm',0,...
'Jm',200e-6,...
'G',-66.6111,...
'B', 1.48e-3, ... % actuator viscous friction coefficient (measured at the motor)
'qlim',[-165 165]*du);
L2=Revolute('offset',pi/2','d',0,'a',0.350,'alpha',0,...
'I',[0.45,0.764,0.539,0,0,0],...
'r',[-0.4638,0.008,0.3925],'m',17.4,...
'Jm',200e-6,...
'G',107.815,...
'B', 1.48e-3, ... % actuator viscous friction coefficient (measured at the motor)
'qlim',[-110 110]*du);
L3=Revolute('d',0,'a',0.042,'alpha',pi/2,...
'I',[0.006,0.07,0.06725,0,0,0],...
'r',[-0.0143,-0.0671,0.089],...
'm',4.8,...
'Jm',200e-6,...
'G',-53.7073,...
'B', 1.48e-3, ... % actuator viscous friction coefficient (measured at the motor)
'qlim',[-110 70]*du);
L4=Revolute('d',0.351,'a',0,'alpha',-pi/2,...
'I', [1.8e-3, 1.3e-3, 1.8e-3, 0, 0, 0],...
'r', [0, 0.019, 0],...
'm', 0.82,...
'Jm', 33e-6,...
'G', 60.0364,...
'B', 1.48e-3, ... % actuator viscous friction coefficient (measured at the motor)
'qlim',[-160 160]*du);
L5=Revolute('d',0,'a',0,'alpha',pi/2,...
'I', [0.3e-3, 0.4e-3, 0.3e-3, 0, 0, 0], ...
'r', [0, 0, 0], ...
'm', 0.32, ...
'Jm', 33e-6, ...
'G', 69.923, ...
'B', 1.48e-3, ... % actuator viscous friction coefficient (measured at the motor)
'qlim',[-120,120]*du);
L6=Revolute('d',0.082,'a',0,'alpha',0,...
'I', [0.15e-3, 0.15e-3, 0.04e-3, 0, 0, 0], ...
'r', [0, 0, 0.032],...
'm', 0.09, ...
'Jm', 33e-6, ...
'G', 78.686, ...
'B', 1.48e-3, ... % actuator viscous friction coefficient (measured at the motor)
'qlim',[-400,400]*du);
Ez=SerialLink([L1,L2,L3,L4,L5,L6]);
Ez.name='ABBIRB1200';
Ez= SerialLink([L1,L2,L3,L4,L5,L6],'name','ABB1200 EzekielMok')
五、 机械臂轨迹规划分析
在笛卡尔空间,输入参量为起点和终点的齐次矩阵,关节空间中,输入参量为 起点和终点的关节变量。 jtraj()函数来进行关节空间的轨迹规划, ctraj()函数进行笛卡尔空间的轨迹规划。
5.1关于关节角度空间的五次样条规划
在此章节中,根据关节角度的给定信号做五次样条规划,具体的实现代码如图所示。

规划后得到的位置,角速度,角加速度,力矩曲线如图所示,可见利用五次样条规划得到的轨迹启动与结束十分平滑,在运行中间达到速度最大,这样能够保证机器人各个关节电机的平稳控制,不会产生电机的急停、摩擦等,该规划方法在实际工程中应用十分广泛。

规划后的空间轨迹如图所示,可见曲线平滑,未出现突变点 。


5.2笛卡尔空间直线规划分析
给定空间两点的位置进行笛卡尔坐标下的五次样条直线规划,并将目标点的坐标通过非完整自由度限制的逆向运动学求解器求解出需要控制的角度信号,并根据信号的变化求出角速度、角加速度与力矩等。



从上述实验可以得出,机械臂在规划好末端的直线轨迹后,五次样条规划好直线路径后,可得到角度的变化圆滑、角速度的反馈信号连续,但是角加速度的反馈信号有突变,这符合电机在实际工程中的应用。相比于关节角度空间下的规划,末端执行器笛卡尔坐标下的轨迹规划更切合应用的实际,因此具有很强的工程实践价值。
5.3笛卡尔空间曲线规划分析
把圆弧规划转化为直线规划,把一个圆弧是看成无穷直线构成的。所以按照这个思路,相邻两点之间用直线规划。为了保持末端轨迹平稳按照预设轨迹运动,需要设计一个控制器,给定每个时刻的速度与位置信号,控制器根据给定与偏差作响应的轨迹跟踪控制。先对机械臂工作空间中的任意选取圆弧进行数学描述,如下所示。


采用分段线性化的方式进行,对该圆弧的轨迹跟踪,具体实现如下:
1、从开始依次增加一个增量时间t=t+ts;
2、利用所选择的轨迹函数,计算出手的位姿;
3、利用机器人逆运动学方程计算对应的关节变量;
4、把关节信息送关节控制器;
5、依次循环

5.4微分运动和速度分析

其中:dx,dy,dz表示机沿x,y,z轴的微分运动δx,δy, δz表示机器人绕x,y,z轴的微分旋转。通过给定末端的角度与特定时刻的速度,可以根据上述公式根据角度空间下速度计算笛卡尔坐标下的微分变量,或者反求。



六、基于Simulink的动力学仿真
在本节中主要对机械臂的前馈与力矩控制进行分析。
6.1前馈控制
在机械臂的电机控制中,除了位置、转速控制之外,为了更高的控制精度与控制性能还应该对力矩加以控制,以适应末端在负载变化的平稳性,所以本节设计了一个前馈控制策略,如图所示,包含一个机械臂关节角度、速度、加速度给定模块,PD控制反馈模块,两个零阶保持器,一个RNE动力学解算模块,和一个机器人模型绘制模块。为简单起见,控制信号给定模块设计为一个关节角度空间规划,此处可以根据机器人实际规划要求设计角度、速度、加速度给定信号。其中RNE 模块将期望的位姿、速度及加速度转为期望的关节力矩,位置和速度的反馈和输入偏差经过控制器后输出控制力矩,二者共同输入到正运动学模块得到输出的位置、速度变量。前馈环节主要来处理扰动,PD控制模块处理与给定的偏差。


根据模型要求进行PD参数调制,可得KP=50与KD=4为较为理想的参数,另外在给定控制信号模块设计的角度与第五章所给定一致,采样时间设置为无限小-1,即为连续。

从实验的动态仿真曲线可以得出,各个关节都能在较短时间内按照给定的控制信号计算出关节控制扭矩,并且震荡幅度较小,前馈的加入能够抵消可测扰动,机械臂各个关节运动平稳,能胜任控制要求。
6.2转矩控制
转矩的仿真在6.1节的章节中去除前馈环节,具体的设计如下:



从实验曲线看出,震荡较为严重,调整PD参数后可得,KP参数较大而KD参数过小时候会出现发散无法收敛的情况,如KP=60,KD=2时系统不稳定,重新调节参数KP=35,KD=10时,系统收敛性良好。


从实验的动态仿真曲线可以得出,各个关节都能在较短时间内按照给定的控制信号计算出关节控制扭矩,并且震荡幅度较小,机械臂各个关节运动平稳,能胜任控制要求。
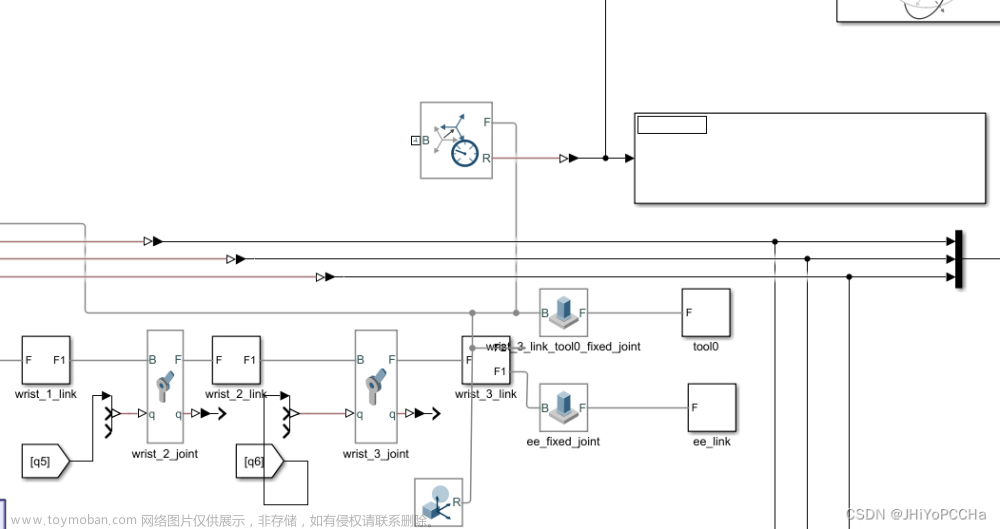
七、Simulink与Adams联合动力学仿真
基于6章中的前馈力矩控制分析,本章通过开源的三维模型,可以通过导入的形式得到机械臂ABB-IRB-1200的Adams虚拟样机模型。对主要的参数进行配置,主要包括机器人零部件的材料属性、约束、驱动、接触力等约束,并设置实验测量指标,收集数据验证实验。最后通过机械控制系统输出步骤可以生成 MATLAB 文件与 Simulink 文件,用于配置 Simulink 与 Adams 联合仿真的通讯连接环境,时间紧凑,只做到两个软件能成功通讯。



 文章来源:https://www.toymoban.com/news/detail-447049.html
文章来源:https://www.toymoban.com/news/detail-447049.html
 文章来源地址https://www.toymoban.com/news/detail-447049.html
文章来源地址https://www.toymoban.com/news/detail-447049.html
到了这里,关于ABB-IRB-1200运动学分析MATLAB RVC工具分析+Simulink-Adams联合仿真的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!