1.案例背景与分析策略
1.1 案例背景介绍
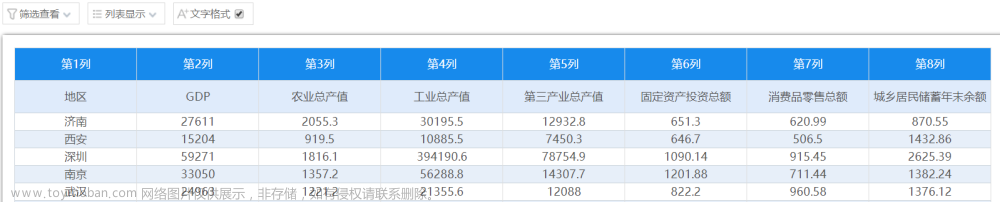
某研究收集到美国50个州关于犯罪率的一组数据,包括人口、面积、收入、文盲率、高中毕业率、霜冻天数、犯罪率共7个指标,现在我们想考察一下州犯罪率和哪些指标有关。数据上传SPSSAU后,在 “我的数据”中查看浏览原始数据,前5行数据如下:

图1 “我的数据”查看浏览数据集
1.2 明确目的与分析策略
从数据分析的目的上,我们想了解犯罪率是否受到人口、面积、收入、文盲率、高中毕业率、霜冻天数6个方面的影响。影响因素分析,可以考虑回归分析、方差分析等统计方法,考虑到目标变量即因变量犯罪率为连续型数据,其他6个指标也为连续型变量,因此考虑尝试拟合多重线性回归模型,用以研究犯罪率的影响因素。
其中,犯罪率作为因变量,其他人口、面积等6个变量作为自变量。为高效分析、精简模型,本例将采用逐步回归的方式由模型自动筛选对因变量有影响的自变量。
2.初步数据分析
2.1 线性关系探查
拿到数据后,不宜马上开始线性回归拟合,应当首先探查各自变量X与因变量Y是否存在线性关系这一基础条件。如果拒绝该条件,则考虑对数据做转换或改用其他统计方法在SPSSAU中,可以借助“散点图”、“Pearson相关系数矩阵”初判X与Y的线性关系是否存在。
在“通用方法”栏目中选择【相关】,将人口~犯罪率共7个变量拖拽至【定量分析项】框中, 默认选择“Pearson相关系数”,最后点击“开始分析”。

图2 自变量、因变量间的相关性
各变量两两间的线性相关系数见图2。人口、文盲率、高中毕业率、霜冻天气与犯罪率存在线性相关(均P值<0.05),是我们重点的研究对象。面积、收入两个指标与犯罪率的相关系数无统计学意义,但考虑到专业经验与既往研究结论认为二者对犯罪率有线性关系,本次案例仍拟将二者作为次要因素参与线性拟合。
X与Y是否有线性关系,建议绘制多变量散点图矩阵,通过散点图观察线性趋势,比相关系数更直观高效。
2.2 共线性问题排查
由图2可知,6个自变量间相关系数绝对值介于(0.023,0.672)之间,初步认为各自变量间无强相关性。
在SPSSAU中,有两处功能可以实现线性回归。“通用方法”栏目下的【线性回归】适用于自变量较少的情况,此时拟考察的自变量将全部进入模型。而“进阶方法”栏目下的【逐步回归】适用于自变量较多的情况,此时众多自变量可以采取逐步回归的策略进入模型。
现在我们可以借助【线性回归】,考察所有6个自变量的多重共线性问题。打开【线性回归】界面,犯罪率移入【定量Y】框,其他6个自变量移入【定量X】框,不勾选“保存残差和预测值”选项,点击“开始分析”。

图3 线性回归系数、VIF、方差分析结果表格
图3中可见各自变量的VIF方差膨胀因子,一般认为VIF低于5(也有说法是低于10)可忽略共线性问题。本例中,VIF最高值为3.911低于5,再结合没有强相关性,初步判断认为,6个自变量间的共线性问题可忽略不计。
3.逐步回归分析
3.1 软件操作
自变量个数较少时,可采取强制纳入的方式,自变量个数较多时,可考虑采取逐步回归。有的研究会根据样本量大小,选择先做一元线性回归,逐个考察单个自变量的影响,然后再选择有显著影响的自变量做多重线性回归。结合相关性结果与样本量,本例拟直接采用逐步回归,接下来做多重线性逐步回归。
在“进阶方法”栏目下,选择【逐步回归】,将犯罪率拖拽至【定量Y】框内,人口、面积等6个自变量拖拽至【定量/定类X】框内。默认勾选【保存残差和预测值】,默认选择【逐步法】进行回归。最后点击“开始分析”即可。

图4 SPSSAU逐步回归操作界面
SPSSAU对用户极为友好,逐步回归的操作只需要拖拽变量即可完成,极大降低新手的操作难度。
3.2 回归结果解读
SPSSAU输出的回归结果表格,是一张整合后的三线表表格,内含回归系数、自变量显著性t检验、模型评价决定系数R评分,以及总体回归模型显著性检验结果。具体见下图5。

图5 逐步回归分析系数、VIF、方差分析结果表格
(1)最终模型中只保留了人口、文盲率,人口、文盲率对犯罪率的影响有统计学意义(t=2.808,p=0.007;t=6.978,p<0.01);面积、收入、高中毕业率、霜冻天数不在模型内,说明这4个自变量对犯罪率的影响无统计学意义。由标准化回归系数可知,对犯罪率的影响,相对而言是文盲率比人口相对要重要。
(2)回归模型:Hat Y = 1.652+0.00022*人口+4.081*文盲率;回归模型总体有统计学意义(F=30.75,P<0.01)。
(3)模型调整后的R平方=0.548,即该回归模型可解释因变量犯罪率变化的54.8%,模型解释能力略先不足。
4.回归残差诊断
除了X与Y线性相关条件外,线性回归还对残差有条件要求。主要表现为要求回归残差独立,回归残差服从正态分布,残差无异方差性。
此前我们要求SPSSAU计算并另存回归模型的残差和预测值数据,这两个新的数据,在 “我的数据”中查看数据即可看到。

图6 “我的数据”查看新计算的残差、预测值数据
Residual为回归残差,Prediction为回归拟合或预测值。
4.1 绘制残差PP图
在“可视化”栏目中,选择【PP图QQ图】,将Residual数据移入【分析项】即可绘制出残差的PP图,用于判断残差是否服从正态分布。
4.2 绘制残差散点图
在“可视化”栏目中,选择【散点图】,将Residual数据移入【定量Y】框,Prediction数据移入【定量X】框,绘制残差散点图,用于判断残差是否无异方差性。
4.3 残差条件结果解读
正态PP图,见下图7。
绝大多数点落在对角线上,即可认为数据近似服从正态分布。本例认为满足该条件。同样地,也可以命令SPSSAU绘制残差数据带正态曲线的直方图,或正态QQ图做判断,其结论均一致。

图7 残差数据的正态PP图

图8 残差诊断散点图
残差散点图,见上图8。散点图上各点的分布均匀离散,没有明显规律性。由此判断,残差无异质性。
此图左上角有一个点偏离较远,可根据实际情况判断是否为异常值。如是,则考虑删去后重新回归。本例略。
对于残差独立性,可以依据图5中DW值做出判断,一般认为DW值在1.7~2.3之间则残差独立(无自相关性)。本例DW=2.18,认为残差独立性满足要求。
至此,残差正态、残差独立、残差无异方差性均满足条件。
5.预测
回归模型建立后,SPSSAU也可以针对模型帮用户实现简单的预测功能。本例的研究目的并不强调预测,这里仅做简单示范。

图9 线性回归预测
如上图9所示,在【逐步回归】的结果页面中,找到【模型预测】,直接输入人口值、文盲率值,我们以California州的数据为例,来做验证。依次输入21198、1.1,预测犯罪率为10.893,本例原始中真值为10.3,有微小误差。
6.总结
线性回归中要求自变量为连续型数据,如果遇到类别型自变量,可酌情转为哑变量然后进行回归。在SPSSAU的“数据处理”栏目下【生存变量】功能中可执行哑变量转换。
另外,如果回归分析出现异常值数据,可在SPSSAU中的“数据处理”栏目下【异常值】功能中进行处理或填补。也或者使用稳健回归(Robust回归进行分析,Robust回归是专门处理异常值情况下的回归模型)。
就本案例来说,以犯罪率为因变量,专业上主张的6个因素,人口、面积、收入、文盲率、高中毕业率、霜冻天数,经多重线性逐步回归分析后,最后我们发现人口、文盲率对犯罪率有显著影响,其他4个自变量对因变量的影响无统计学意义。文章来源:https://www.toymoban.com/news/detail-447850.html
本例未对异常值进行识别和处理,实践中应当重视异常数据对回归模型的影响。文章来源地址https://www.toymoban.com/news/detail-447850.html
到了这里,关于手把手教你做多重线性逐步回归的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!