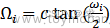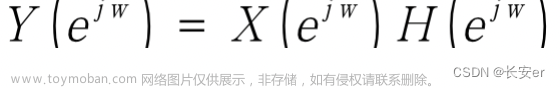一、 实验目的
1.1.1掌握用窗函数法设计FIR数字滤波器的原理和方法。
1.1.2熟悉线性相位FIR数字滤波器特性。
1.1.3了解各种窗函数对滤波特性的影响。
- 实验原理
窗函数设计法的基本原理是用有限长单位脉冲序列逼近与。由于往往是无限长序列，且是非因果的，所以用窗函数将截断，并进行加权处理：
用窗函数设计的滤波器性能取决于窗函数的类型及窗口长度N的取值。设计过程中，要根据阻带最小衰减和过渡带宽度的要求选择合适的窗函数类型和窗口长度N
- 实验设备与器件
计算机、matlab软件。
- 实验内容与步骤
(1)复习用窗函数法设计FIR数字滤波器一节内容。
(2)编写程序
①编写能产生矩形窗、升余弦窗、改进升余弦窗和二阶升余弦窗的窗函数程序。
②编写主程序。
(3)上机实验内容。
①用升余弦窗设计一线性相位低通FIR数字滤波器，截止频率pi/4。窗口长度N＝15,33。要求在两种窗口长度情况下，分别求出(n)，打印出相应的幅频特性和相频特性曲线，观察3dB带宽和20dB带宽。总结窗口长度N对滤波特性的影响。
②,用四种窗函数设计线性相位低通滤波器。绘制相应的幅频特性曲线，观察3dB和20 dB带宽以及阻带最小衰减，比较四种窗函数对滤波器特性的影响。
- 数据记录
用升余弦窗设计一个FIR数字滤波器，把窗口长度分别设置为N=15，N=33，打印出来的脉冲响应如图1所示，幅频特性曲线和相频特性曲线如下图所示
我们可以清楚地看出，对于同一类窗函数来说，窗口长度越大，过渡带越窄，而阻带的衰减不受窗函数长度N的影响。即过渡带的宽度（近似等于主瓣宽度）随窗宽增加而减少。
图 窗口长度不同时的频率特性曲线
窗口长度为N=33，截止频率为pi/4时的四种窗函数的线性相位低通滤波器的比较如图所示，我们可以看出，矩形窗的过渡带最窄，二阶升余弦窗的过渡带最宽。而阻带的衰减则是矩形窗最小，二阶升余弦窗最大，升余弦窗和改进的升余弦窗在他们两个之间，因此可以得出，过渡带的宽度与阻带的衰减时不可以兼具的，必须要实现一个折中。
文章来源：https://www.toymoban.com/news/detail-448083.html
图 不同窗函数的频率响应曲线文章来源地址https://www.toymoban.com/news/detail-448083.html
%%
clc
close all
%升余弦窗函数N=15/33滤波
wc=pi/4; N1=15;N2=33;
hd1= ideallp1(wc,N1); % 用wc=0.2*pi的理想低通作为逼近滤波器
hd2= ideallp2(wc,N2); % 用wc=0.2*pi的理想低通作为逼近滤波器
wd1=hanning(N1)'; b1=hd1.*wd1; % 用升余弦窗设计：
wd2=hanning(N2)'; b2=hd2.*wd2; % 用升余弦窗设计：
[H1,w1]=freqz(b1,1);
[H2,w2]=freqz(b2,1);
figure(1)
subplot(211),stem(b1);
title('窗宽度为15的脉冲响应')
subplot(212),stem(b2);
title('窗宽度为33的脉冲响应')
figure(2)
subplot(2,1,1), plot(w1,20*log10(abs(H1)),w2,20*log10(abs(H2)),'-.');% 绘幅特性
xlabel('\omega'),ylabel('|H(\omega)|'),title('幅频特性曲线')
legend('N=15','N=33')
subplot(2,1,2), plot(w1,angle(H1),w2,angle(H2),'-.');
xlabel('\omega'),ylabel('rad'),title('相频特性曲线')
legend('N=15','N=33')
figure
%%
%%
%四种窗函数
wc=pi/4;N1=33;
hd1=ideallp1(wc,N1);
wd1=boxcar(N1)' ; b1=hd1.*wd1; % 用矩形窗设计：
wd2=hanning(N1)'; b2=hd1.*wd2; % 用升余弦窗设计：
wd3=hamming(N1)'; b3=hd1.*wd3; %用改进的升余弦窗设计
wd4=blackman(N1)';b4=hd1.*wd4; % 用二阶升余弦窗设计：
[H1,w]=freqz(b1,1); % 用矩形窗设计的频率特性
[H2,w]=freqz(b2,1); % 用升余弦窗设计的频率特性
[H3,w]=freqz(b3,1); % 用改进的升余弦窗设计的频率特性
[H4,w]=freqz(b4,1); % 用二阶升余弦窗设计的频率特性
figure(3)
%幅频特性
subplot(2,1,1),plot(w,20*log10(abs(H1)),w,20*log10(abs(H2)),':',w,20*log10(abs(H3)),'-.',w,20*log10(abs(H4)),'-.');
legend('矩形窗','升余弦窗','改进的升余弦窗','二阶升余弦窗')
xlabel('\omega'),ylabel('|H(\omega)|'),title('幅频特性曲线')
% 相频特性
subplot(2,1,2),plot(w,angle(H1),w,angle(H2),':',w,angle(H3),'-.',w,angle(H4),'-.');
legend('矩形窗','汉宁窗','布莱克曼窗')
legend('矩形窗','升余弦窗','改进的升余弦窗','二阶升余弦窗')
xlabel('\omega'),ylabel('rad'),title('相频特性曲线')
%%
%理想滤波器频率响应
function hd1=ideallp1(wc,N1)
tao=(N1-1)/2;
n=[0:(N1-1)];
m=n-tao+eps;
hd1=sin(wc*m)./(pi*m);
end
function hd2=ideallp2(wc,N2)
tao=(N2-1)/2;
n=[0:(N2-1)];
m=n-tao+eps;
hd2=sin(wc*m)./(pi*m);
end
到了这里，关于窗函数法设计FIR数字滤波器的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
