前言
研一生活开始了，看了大家对我之前博客的鼓励让我知道写博客是一件多么有意义的事情。写这些让我遇见许多陌生的有缘人，有老骥伏枥的大叔、也有可爱温暖的学妹……
这里将高等工程数学的笔记留给不爱吃香菜的月亮，希望这些陪伴过我的微光在明年也能照亮她的研途。
第一章 （1）距离与范数
距离的定义和性质
- 非负性、对称性、三角不等式。这三条性质用来证明是否为距离。
范数与赋范空间的定义
- 范数是具有长度概念的函数
- 完备的赋范线性空间称为Banach空间
內积
我们从多个角度来看內积的概念。
代数角度
设二维空间内有两个向量 a ⃗ = ( x 1 , y 1 ) \vec{a}=(x_1 , y_1) a=(x1,y1) 和 b ⃗ = ( x 2 , y 2 ) \vec{b}=(x_2 , y_2) b=(x2,y2)，定义它们的点积为以下实数： a ⃗ ⋅ b ⃗ = x 1 ⋅ y 1 + x 2 ⋅ y 2 \vec{a} \cdot \vec{b} = x_1\cdot y_1 + x_2\cdot y_2 a⋅b=x1⋅y1+x2⋅y2
几何角度
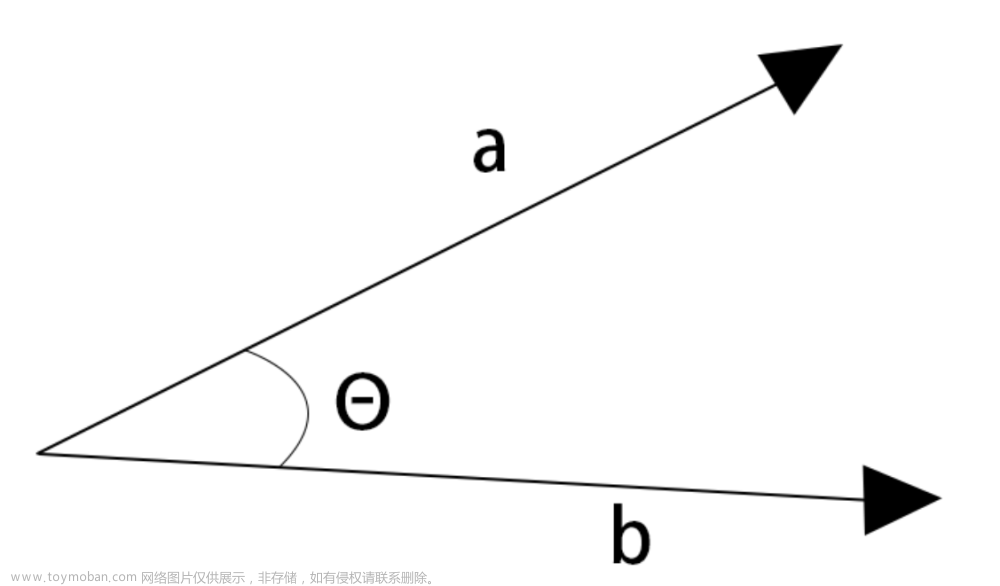
设二维空间内有两个向量 a ⃗ \vec{a} a 和 b ⃗ \vec{b} b。它们的夹角为 θ \theta θ （ 0 < θ < Π 0 < \theta <\Pi 0<θ<Π）则内积定义为以下实数： a ⃗ ⋅ b ⃗ = ∣ a ⃗ ∣ ∣ b ⃗ ∣ c o s θ \vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}|cos\theta a⋅b=∣a∣∣b∣cosθ ，其实就是投影后相乘。该定义只对二维和三维空间有效。
等价范数
- 同时，有限维空间上的任何两个范数必是等价的。
向量范数
- 向量范数和矩阵范数是有联系的。可以将向量看做是一个只有一行的矩阵，除了第一个维度其他维度全是0，所以在变换时就坍塌到了一维。例如，对于 ∞ \infty ∞范数而言这里其实还要乘以维数，只不过对于向量而言维数为1。
矩阵范数
- 矩阵范数相比范数的定义加了一个相容性
- 跟刚才的向量的范数对比下会发现很像
- 这里 t r A trA trA代表方阵 A 的迹（A 的主对角线上元素之和）
矩阵范数和向量范数的相容性
- 向量1范数与矩阵 m 1 m_1 m1范数相容
- 向量2范数与矩阵F范数相容
- 向量1，2， ∞ \infty ∞范数均与矩阵 m ∞ m_\infty m∞范数相容
- 任何向量范数都存在与之相容的矩阵范数（算子范数）
酉矩阵
定义
- 即 U H = U − 1 U^H = U^{-1} UH=U−1
性质
F范数的酉不变性
正规矩阵
文章来源：https://www.toymoban.com/news/detail-448296.html
例：
文章来源地址https://www.toymoban.com/news/detail-448296.html
到了这里，关于高等工程数学 —— 第一章 （1）距离与范数的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
