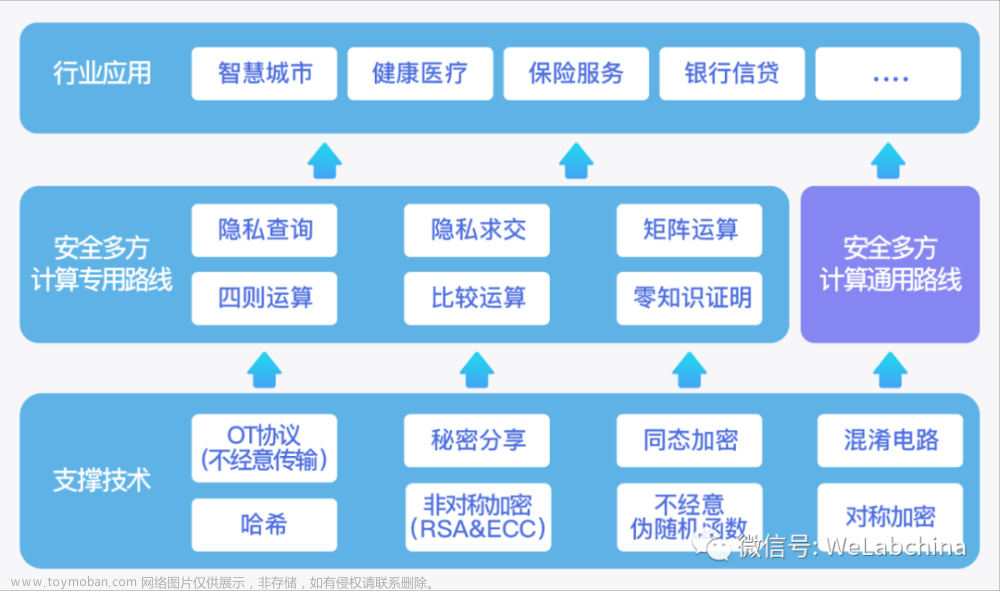
【安全多方计算】百万富翁问题
【问题描述】
百万富翁问题是姚期智先生在1982年提出的第一个安全双方计算问题,两个百万富翁街头邂逅,他们都想炫一下富,比比谁更有钱,但是出于隐私,都不想让对方知道自己到底拥有多少财富,所以要在不借助第三方的情况下,知道他们之间谁更有钱。
【问题分析】
①这里假设Alice和Bob就是这两个百万富翁,Alice拥有财富i百万,Bob拥有财富j百万,假设他们两的财富都没有超过N百万,即1 ≤ i , j ≤ N,如下图所示:

②Alice随机选择一个大随机数x,用Bob的公钥加密后得到x的密文c,如下图所示:

③Alice将c-i发送给Bob(减去i是为了破坏密文c),如下图所示:

④Bob首先计算N个数:yu=DSKB(c-i+u), 其中u=1,2…N(这里加上u是为了能在yu的数列里面还原出被破坏的密文),然后随机选择一个大素数p,再计算N个数:zu=yu mod p, 其中u=1,2…N,如下图所示:

⑤接着Bob对于所有的0≤a≠b≤N,是否都满足|za-zb|≥2(如果小于2的话,就可能导致第⑥步里面的数串,zj+1+1,zj+2+1,…,zN+1和zj+1相等),若不满足,则重新选择大素数p并重新验证。如下图所示:

⑥如果满足,Bob将以下的N个数串和p:(z1,z2,…,zj,zj+1+1,zj+2+1,…,zN+1,p)一起发给Alice(这里从zj+1开始每一项+1是为了在第⑦步Alice验证的时候能得出正确的结论,而且也保护了Bob的隐私,不能泄露j的值),如下图所示:

⑦假设Alice收到这N+1个数的第i个数满足Zi=x(mod p),则结论是i≤j,否则i>j(对应第④步中的zu=yu mod p)。如下图所示:
【代码实现】
这部分的算法思想参考了csdn上Bertramoon的博客,只不过这里换成java实现。
【前导模块】
1.判断素数
public static boolean is_prime(int x) throws Exception {//判断素数
if (x <= 1) {
throw new Exception("0和1既不是素数也不是合数,x应为大于1的正整数");
}
for(int i = 2; i < (int) (Math.sqrt(x) + 1); i++) {
if(x % i == 0) {
return false;
}
}
return true;
}
2.求最大公约数
public static int gcd(int a,int b) {//求最大公约数
if (b == 0) {
return a;
} else {
return gcd(b, a % b);
}
3.求乘法逆元
首先,数学上的乘法逆元就是指直观的倒数,即 a 的逆元是 1/a,也即与 a 相乘得 1 的数。ax=1,则x是a的乘法逆元。
这里我们讨论关于取模运算的乘法逆元,即对于整数 a,与 a 互质的数 b 作为模数,当整数 x 满足 ax mod b≡1 时,称 x 为 a 关于模 b 的逆元,代码表示就是a*x % b == 1。

这部分的实现代码如下:
public static int[] get_inverse(int a, int b){
// a*x = 1 mod b
// b*y = 1 mod a
// 已知a、b,返回x, y
if (b == 0) {
int [] l = {1, 0};
return l;
} else {
int [] r = get_inverse(b, a % b);
int x1, x2, y1, y2;
x2 = r[0];
y2 = r[1];
x1 = y2;
y1 = x2 - ((int)a / b) * y2;
int [] r2 = {x1, y1};
return r2;
}
}
4.生成公钥和私钥
-
随机生成两个大素数p 、 q ( p ! = q ) ;
-
n = p ∗ q , s = ( p − 1 ) ∗ ( q − 1 ) ;
-
随机取一个大整数e ,使得2 ≤ e ≤ s − 1且 g c d ( e , s ) = 1;
-
用扩展欧几里得算法求e 的乘法逆元 d ( e ∗ d = 1 m o d s , d > 0 ) ;
-
公钥为( n , e ),私钥为( n , d );
public static int [][] create_key() throws Exception {
// 创建公钥和私钥
int p, q, n, s;
while (true) {
p = new Random().nextInt(90) + 10;
if (is_prime(p)) {
break;
}
}
while (true) {
q = new Random().nextInt(90) + 10;
if (is_prime(q) && q != p) {
break;
}
}
n = p * q;
s = (p - 1)*(q - 1);
int d,e;
System.out.println("n="+String.valueOf(n)+",s="+String.valueOf(s));
while (true) {
e = new Random().nextInt(s - 3) + 2;
if (gcd(e, s) == 1){
d = get_inverse(e,s)[0];
if (d>0){
break;
}
}
}
int [][] r = {{n,e},{n,d}};
return r;
}
【总体实现】
import java.math.BigInteger;
import java.util.Random;
import java.util.Scanner;
public class millionaire{
public static void main(String[] args) throws Exception {
// Alice的财富为i,Bob的财富为j,取值为0~10
// Alice选择一个随机大整数x
// Alice和Bob约定使用RSA算法
// Bob用RSA算法生成公钥和私钥,将公钥发给Alice
// Alice使用Bob的公钥加密x得C=E(x),并发送C-i给Bob
// Bob使用私钥计算Y(u) = D(C-i+u) (1<=u<=10)
// Bob随机取一个小于x的大整数p,将Y(u) mod p得到Z(u),验证对所有Z(u)都满足0<Z(u)<p-1。若不满足则更换p重新计算
// 再将Z(u)从第j-1位开始向右均+1得到K(u),然后将K(u)和p发给Alice
// Alice将K[i-1]与(x mod p)进行比较,如果相等,则说明i<j,即Alice不如Bob富有;若不相等,则说明i>=j,说明Alice比BOb富有或者和Bob一样富有
Scanner input = new Scanner(System.in);
System.out.print("Alice:");
int i = input.nextInt();
System.out.print("Bob:");
int j = input.nextInt();
int x;
while (true) {
x = new Random().nextInt(90) + 10;
if (is_prime(x)){
break;
}
}
System.out.println("随机整数x="+String.valueOf(x));
int [] pbk, pvk;
int [][] r = create_key();
pbk = r[0];
pvk = r[1];
System.out.println("公钥(n,e)=("+String.valueOf(pbk[0])+","+String.valueOf(pbk[1])+")\n"+
"私钥(n,d)=("+String.valueOf(pvk[0])+","+String.valueOf(pvk[1])+")");
int C = encrypt(x, pbk);
System.out.println("Alice发送C-i="+String.valueOf(C - i)+"给Bob");
int [] Y = new int[10];
for(int u = 1; u<11;u++){
Y[u - 1] = decrypt(C-i+u,pvk);
}
System.out.println("Y="+toS(Y).toString());
int p = new Random().nextInt(x - 11) + 10;
int [] Z = new int[10];
while (true) {
for(int u = 0; u<10;u++){
Z[u] = Y[u] % p;
}
if(max(Z) < p -1 &&min(Z)>0){
break;
}
p = new Random().nextInt(x - 11) + 10;
}
System.out.println("p="+String.valueOf(p)+"\nZ="+toS(Z).toString());
for(int u=0;u<10;u++){
if(u>=j+1){
Z[u] = Z[u] + 1;
}
}
System.out.println("k="+toS(Z).toString());
if(Z[i-1] == x % p){
if (i<j){
System.out.println("Bob更富有");
}else {
System.out.println("验证错误,i应该大于j,Alice可能更富有,也可能和Bob一样富有");
}
}else {
if (i >= j){
System.out.println("Alice可能更富有,也可能和Bob一样富有");
}else {
System.out.println("验证错误,j应该大于i,Bob更富有才对");
}
}
}
public static StringBuffer toS(int []d){
StringBuffer stringBuffer = new StringBuffer();
stringBuffer.append("[ ");
for (int i=0;i<d.length;i++){
stringBuffer.append(d[i]);
stringBuffer.append(" ");
}
stringBuffer.append(" ]");
return stringBuffer;
}
public static int gcd(int n, int m){
int z = 0;
while (m%n != 0){
z = m%n;
m = n;
n = z;
}
return n;
}
public static int max(int []d){
int m = d[0];
for (int i = 1; i<d.length;i++){
if(m<d[i]){
m = d[i];
}
}
return m;
}
public static int min(int []d){
int m = d[0];
for (int i = 1; i<d.length;i++){
if(m>d[i]){
m = d[i];
}
}
return m;
}
public static boolean is_prime(int x) throws Exception {
if (x <= 1) {
throw new Exception("0和1既不是素数也不是合数,x应为大于1的正整数");
}
for(int i = 2; i < (int) (Math.sqrt(x) + 1); i++) {
if(x % i == 0) {
return false;
}
}
return true;
}
public static int[] get_inverse(int a, int b){
// a*x = 1 mod b
// b*y = 1 mod a
// 已知a、b,返回x, y
if (b == 0) {
int [] l = {1, 0};
return l;
} else {
int [] r = get_inverse(b, a % b);
int x1, x2, y1, y2;
x2 = r[0];
y2 = r[1];
x1 = y2;
y1 = x2 - ((int)a / b) * y2;
int [] r2 = {x1, y1};
return r2;
}
}
public static int [][] create_key() throws Exception {
// 创建公钥和私钥
int p, q, n, s;
while (true) {
p = new Random().nextInt(90) + 10;
if (is_prime(p)) {
break;
}
}
while (true) {
q = new Random().nextInt(90) + 10;
if (is_prime(q) && q != p) {
break;
}
}
n = p * q;
s = (p - 1)*(q - 1);
int d,e;
System.out.println("n="+String.valueOf(n)+",s="+String.valueOf(s));
while (true) {
e = new Random().nextInt(s - 3) + 2;
if (gcd(e, s) == 1){
d = get_inverse(e,s)[0];
if (d>0){
break;
}
}
}
int [][] r = {{n,e},{n,d}};
return r;
}
public static int encrypt(int content, int [] pbkey){
BigInteger c = new BigInteger(String.valueOf(content));
BigInteger p0 = new BigInteger(String.valueOf(pbkey[0]));
int r = (c.pow(pbkey[1]).mod(p0)).intValue();
return r;
// return (int)Math.pow(content, pbkey[1]) % pbkey[0];
}
public static int decrypt(int encrypt_content, int [] pvkey){
BigInteger c = new BigInteger(String.valueOf(encrypt_content));
BigInteger p0 = new BigInteger(String.valueOf(pvkey[0]));
int r = (c.pow(pvkey[1]).mod(p0)).intValue();
return r;
// return (int)Math.pow(encrypt_content, pvkey[1]) % pvkey[0];
}
}
【测试结果】

 文章来源:https://www.toymoban.com/news/detail-448742.html
文章来源:https://www.toymoban.com/news/detail-448742.html
ps:本人也是这方面知识的初学者,如果有什么认识不到位或者错误的地方恳请批评指正。文章来源地址https://www.toymoban.com/news/detail-448742.html
到了这里,关于【安全多方计算】百万富翁问题的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!