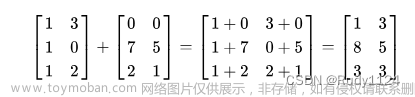
尽管AI的发展取得了巨大进步，但编译器LLVM之父Chris Lattner认为，AI技术应用并不深入，远远没有发挥出已有机器学习研究的所有潜力。而AI系统和工具的单一化和碎片化正是造成这一问题的根源。
为了让AI发挥其真正的潜力，计算碎片化是需要解决的重点问题之一，目标是让AI软件开发人员能够无缝地充分利用现有硬件和下一代创新硬件。但解决这一问题并不容易，硬件、模型和数据的多样性使得当前市场上的现有解决方案都只是单点性质的，Chris Lattner创立的Modular团队从矩阵算法的角度对此进行了深入分析。
（以下内容由OneFlow编译发布，译文转载请联系OneFlow获得授权。https://www.modular.com/blog/ais-compute-fragmentation-what-matrix-multiplication-teaches-us）
作者｜Eric Johnson、Abdul Dakkak、Chad Jarvis
OneFlow编译
翻译｜徐佳渝、杨婷
1
算力碎片化正在阻碍AI的发展
AI由数据、算法（即模型）和算力驱动，三者之间形成了良性循环。其中任意一方的发展会推动其他方面需求的增长，从而严重影响开发者在可用性和性能等方面的体验。如今，我们拥有更多的数据，做了更多的AI模型研究，但算力的扩展速度却没有跟上，这主要是由于物理限制。
如果你一直在关注AI和硬件的发展，可能听说过摩尔定律时代即将结束。过去60年，单核处理器每18个月翻一倍性能提升速度的情况已然改变。除了继续制造越来越小的晶体管的物理限制之外（例如，电流泄漏会导致功耗过高，从而引起发热），性能也越来越多地受到内存延迟的限制，而这种限制的增长速度比处理速度要缓慢得多。
（Hennessy和Patterson的图灵演讲：不同时期CPU处理器性能提升的分析（性能提升的速度保持稳定））
然而，随着模型不断扩大，在边缘计算中创建和处理的企业数据更多，对AI计算的需求也在不断增加。因此，尽可能地利用硬件设备的性能已成为业界的关注焦点。
文章来源：https://www.toymoban.com/news/detail-448919.html
（机器学习三个时代的算力走向（https://arxiv.org/pdf/2202.05924.pdf），Sevilla：计算需求随时间呈对数方式变化的分析。其中，2010年左文章来源地址https://www.toymoban.com/news/detail-448919.html
到了这里，关于AI算力碎片化：矩阵乘法的启示的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
