【离散数学期复习系列】四、图-Toy模板网

这篇具有很好参考价值的文章主要介绍了【离散数学期复习系列】四、图。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

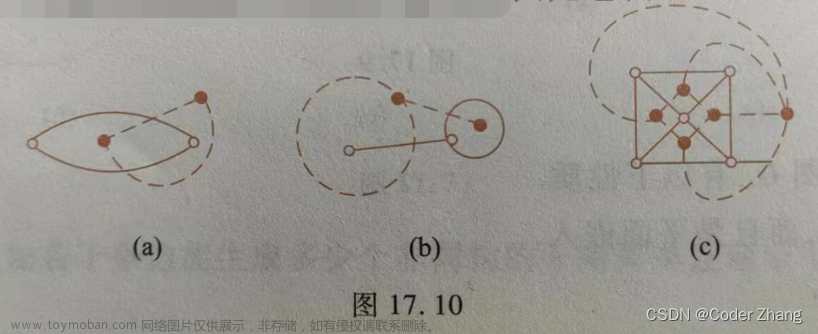
1.无序积: 设A、B为两集合,称{{a ,b} | a ∈A∧b∈B}为A与B的无序积,记作A&B.,将无序对{a ,b}
记作(a ,b)，且(a ,b)=(b,a)
多重集：有重复元素的集合
2.
(1)无向图:
一个无向图G是一个二元组〈V,E〉,其中
1)V是一个非空的有穷集合,称为.G的顶点集,V中元素称为顶点或结点;
2)E是无序积V&V的一个多重子集,称为G的边集,E中元素称为无向边或简称边.
图G的顶点集记作V(G),边集记作E(G)

(2)空图:规定顶点集为的∅图为空图

(3)有向图:
一个有向图D是一个二元组〈V,E〉,其中
1)V是一个非空的有穷集合,称为D的顶点集,V中元素称为顶点或结点;
2)E是卡氏积VXV的多重子图,称为D的边集，其元素称为有向边,也简称边.
【离散数学期复习系列】四、图

注:常用G表示无向图边集合用{(a,b)},D表示有向图,边集合用{<a,b>}
(4)n阶图:n个顶点的图
(5)零图:没有一条边的图
(6)平凡图(一阶零图):只有一个顶点,没有边的图

3.无向图和有向图相关描述
(1)在无向图G=<V,E>中，
设e=(u,v)是的一条边,则称u,v为e的端点,e与u(和v)关联．
无边关联的顶点称为孤立点.
若一条边所关联的两个顶点重合,则称此边为环.
若u≠v,则称e与u(和v)的关联次数为1;
若u=v,称e与u的关联次数为2;
若w不是e的端点,则称e与w的关联次数为0.
若存在一条边e以顶点u ,v为端点,则称u,v是相邻的.若两条边e ,e’至少有一个公共端点,则称e ,e’是相邻的.
边与点是关联
点与点是相邻
边与边的相邻
(2)在有向图D=<V,E>中,设e=(u,v)是的一条有向边,则称u为e的始点，v为e的终点，也称u,v为e的端点,e与u(和v)关联．无边关联的顶点称为孤立点.若一条有向边的始点与终点重合,则称此边为环.

(1)度数:简称度,顶点v作为边的端点的次数之和,记为d(v)
【离散数学期复习系列】四、图

（5）是最大度（6）是最小度
【离散数学期复习系列】四、图

(1)握手定理:设图G=(V,E)为无向图或有向图,V={v1 , v2 ,…, vn },边数|E|=m,无向图则度数等于边数的两倍
【离散数学期复习系列】四、图

(2)有向图则各顶点出度之和等于入度之和等于边数
【离散数学期复习系列】四、图

(3)推论:任何图(无向的或有向图)中,度数为奇数的顶点个数是偶数.
(4)度数序列:设V={v1 ,v2 ,…,vn,}为图G的顶点集,称(d(v1),d(v2), …, d(vn))为G的度数序列.

7.(1)平行边:
1)无向图:如果关联一对顶点的无向边多于1条，则称这些边为平行边
2)有向图:如果有多于1条的边的始点与终点相同,则称这些边为有向平行边
(2)重数:平行边的条数
(3)多重图:含平行边的图
(4)简单图:不含平行边也不含环的图
(5)n阶无向完全图:各顶点之间都有边相连记为K n
每个顶点的度都为n-1
边=n（n-1）/2
(6)n阶有向完全图:各顶点之间都有两条方向相反的边
每个顶点的出度和入度都为n-1
边=n（n-1）
(7)子图/母图:图A的顶点和边都含于图B顶点和边,则A是B的子图,B是A的母图,记为A含于 B
真子图:图A含于图B但不等于图B
(8)生成子图（顶点相同）:A是B的生成子图，则A与B的顶点相等,A边含于B的边集,边可少

(9)导出子图:
1)边导出子图:图A的边含于图B,A边不为空,记为G[E]
2)顶点导出子图:图A的顶点含于图B,A顶点不为空G[V]
注:每个图都是自己的子图
【离散数学期复习系列】四、图

(10)补图:设A为n阶无向简单图,A的无向完全图去除A的边,为其补图,记为
【离散数学期复习系列】四、图

补图是相互的，互为补图的两个图顶点是相等的，两个图的边集没有交集

互为补图的两个图合起来是一个完全图
(11)同构:点和边相同，度数序列相同是两图同构的必要条件 G1≌G2
【离散数学期复习系列】四、图

(1)通路:能从一个点v0走到另一个点vl的路，v0为起点，vl为终点,所走的边数为其长度
回路就是起点终点相同:v0=vl
【离散数学期复习系列】四、图

(2)简单通路:经过的边不同(欧拉)
(3)简单回路:v0=vl且边只能走一次,顶点不限
(4)初级通路:除起点和终点外的每个顶点和边都只能走一次
(5)初级回路(圈):v0=vl且每个顶点和边都只能走一次
(6)复杂通路:顶点和边都可以走多次
(7)复杂回路:v0=vl且顶点和边都可以走多次
通路>复杂通路>简单通路>初级通路
【离散数学期复习系列】四、图

9.定理:
(1)在一个n阶图中,若从顶点u到v(u≠v)存在通路,则从u到v存在长度小于等于n-1的（初级）通路.
(2)在一个n阶图中,如果存在v到自身的回路,则存在v到自身长度小于等于n的（初级）回路.

(1)连通:无向图中,顶点u到v存在通路,则称u与v是连通的,任何顶点与自身都是连通的
(2)可达:有向图中,顶点u到v存在通路,则称u可达v
(3)连通分支（极大连通子图）:一个图中每个连通图,记为G[V1],G[V2],…,G[Vk],连通分支个数p(G)
例:下图知,p(G)=3
【离散数学期复习系列】四、图

图中母图显然不是连通的
连通图的连通子图是它自己

(4)连通图:若无向图G是平凡图（只有一个顶点）或G中任意两顶点都是连通的，否则非连通图
(5)弱连通图:有向图D,略去方向后所得无向图是连通图
(6)单向连通图:任意两个顶点至少有一个可达另一个
(7)强连通图:任何一对顶点相互可达
【离散数学期复习系列】四、图

注:无向图分为连通图和非连通图
有向图分为弱连通图<单向连通图<强连通图

(1)删除V’:删除图中的顶点集V’及其关联边
删除E’:删除图中的边集E’
(2)点割集:一个顶点集,图G去掉这个顶点集的顶点后,连通分支个数>原图的连通分支个数,且图G去掉这个顶点集的所有真子集的顶点后,其连通分支个数=原图的连通分支个数（意思就是割集中的点不能再少了，再少就割不了，如果还能再少就不是割集）,称为点割集
如果这个图是本身是连通图，那么它的连通分支只有一个，就是它自己
它被割点割掉之后，连通分支的个数大于2
割点:点割集只有一个点
(3)边割集:一个边集,图G去掉这个边集的边后,连通分支个数>原图的连通分支个数,且图G去掉这个顶点的所有真子集的边后,其连通分支个数=原图的连通分支个数,称为边割集
割边(桥):边割集只有一个边
【离散数学期复习系列】四、图

12.关联矩阵
(1)无向图关联矩阵:
行作为顶点
列作为边
矩阵元素aij:顶点与边的关联次数
【离散数学期复习系列】四、图

性质:(1)列之和都为2,因为每条边都只有两个端点
(2)行之和是该顶点的度数
(3)所有元素之和是总度数
(4)孤立点没有关联边,所以行元素都是0
(5)平行边则有两列元素相同
【离散数学期复习系列】四、图

(2)有向图关联矩阵
行作为顶点
列作为边
矩阵元素aij:1:始点 0未关联 -1终点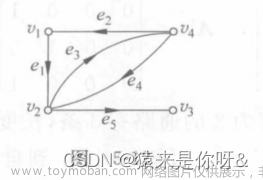
【离散数学期复习系列】四、图

性质:
1)每一列都只有一个1和一个-1,因为边只有一个始点和一个终点
2)每行1的个数代表该点出度个数,-1的个数代表该点入度个数
3)矩阵所有元素1的个数代表总出度=m,-1个数代表总入度=m（m为边数）
【离散数学期复习系列】四、图

(3)邻接矩阵
有向图的邻接矩阵
行列为顶点
元素pij为一个顶点邻接到另一个顶点的边数
【离散数学期复习系列】四、图

性质:（行顶点到列顶点为入度，列顶点到行顶点为出度）
1)行元素之和代表该顶点出度数
2)列元素之和代表该顶点入度数
3)总元素之和代表边数m（总出度和总入度）
【离散数学期复习系列】四、图

推论:
【离散数学期复习系列】四、图

(4)有向图的可达矩阵
行列为顶点
元素pij为是否可达 1可达 0不可达
【离散数学期复习系列】四、图

邻接矩阵和可达矩阵的区别在于：可达矩阵只关心是否可达，不关心有几条通路可达
【离散数学期复习系列】四、图

任何顶点到自身都是可达的

13.最短路径
(1)带权图:给图每条边附加一个实数,G连同附加在边上的实数称为带权图,记为G= <V,E,W>
权:W={w(e)|e∈E},w(e)是附加在e上的实数,称作边e的权

(2)最短路径（权值最小）:设u、v为G中的两个顶点,从u到v的所有通路中权最小的通路称为u到v的最短路径，u到v的最短路径的权称作u到v的距离，记作d(u, v).
(3)最短路径问题:任给一个简单带权图G=<V,E,W>及u ,v∈V,求u,v之间的最短路径及距离.
解:dijkstra算法
1)设(d,v) d为出发点到当前点的总距离,v为上一个经过的顶点
2)确定出发点,该顶点初始值设为(0,λ),其他点为(+∞,λ)
3)每行确定一个最短距离的顶点作为确定点,下一行计算每一个顶点与确定点的距离,与上一行点到初始点的距离取最短距离作为当前值

例:
【离散数学期复习系列】四、图