DP杂谈【持续更新中】-Toy模板网

这篇具有很好参考价值的文章主要介绍了DP杂谈【持续更新中】。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

什么是DP？

推荐看一下。

正文

滚动数组优化

在一些空间贼小，时间还好的 DP 题目里，会用到优化空间的小技♂巧——滚动数组优化。

滚动数组，顾名思义，一个会滚动的数组，主要是怎样个滚法呢？接下来我先举一个例子：

e.g

最长公共子序列（LCS）

给出两个整数序列，求这两个序列的†最长公共子序列。
†最长公共子序列：多个序列的共有的最长子序列。

这道题我们不难发现：
我们设 \(f_{i,j}\) 为从 \(1\) 到 \(i\) 的 \(a\) 子序列和从 \(1\) 到 \(j\) 的 \(b\) 子序列的 \(LCS\)。
它的状态转移方程即为

\[f_{i,j}= \begin{cases} f_{i-1, j-1} + 1 & a[i]=b[j] \\ max(f_{i-1,j},f_{i,j-1}) & a[i]\ne b[j] \end{cases} \]

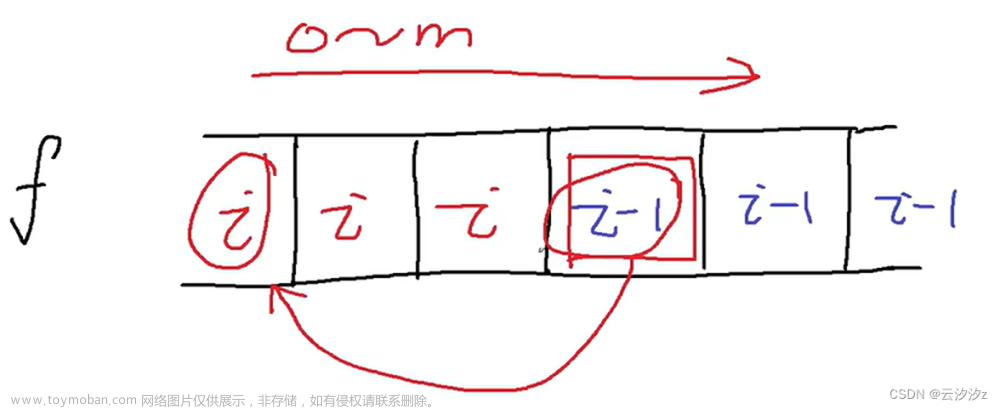
我们发现，状态 \(f_{i,j}\) 只依赖于 \(f_{i-1,\dots}\) 和 \(f_{i,\dots}\)，那么既然 \(i-2\) 及以后的状态都没用了，那么我们可以把那之前的状态给滚掉，即把第一维套上个 \(\% 2\)，思考一下，这里十分的巧妙。

因为 \(mod\) 常数很大，我们为了优化常数，可以使用位运算，即 \(i\% 2\rightarrow i\&1\)，\((i-1)\% 2\rightarrow (i\oplus1)\&1\)

这样我们将巨大的 \(O(n^2)\) 的空间压缩到了 \(O(n)\)。

费用提前计算

在一些题目里，它状态的每一次转移都会产生后效性，所以用普通的DP是做不了的，那么，我们如何解决这个问题呢？

这时，我们有一种策略，就是既然我已经知道未来会被现在影响，那么为什么我不先把将要影响的算了呢？这，就是费用提前计算。

e.g

Luogu 2365 任务安排
题目描述
\(n\) 个任务排成一个序列在一台机器上等待完成（顺序不得改变），这 \(n\) 个任务被分成若干批，每批包含相邻的若干任务。
从零时刻开始，这些任务被分批加工，第 \(i\) 个任务单独完成所需的时间为 \(t_i\)。在每批任务开始前，机器需要启动时间 \(s\)，而完成这批任务所需的时间是各个任务需要时间的总和（同一批任务将在同一时刻完成）。
每个任务的费用是它的完成时刻乘以一个费用系数 \(f_i\)。请确定一个分组方案，使得总费用最小。
对于 \(100\%\) 的数据，\(1\le n \le 5000\)，\(0 \le s \le 50\)，\(1\le t_i,f_i \le 100\)。

我们先设 \(dp_i\) 为前 \(i\) 天的答案，\(time_i\) 为前 \(i\) 天完成后的时间，经过手玩样例过后发现状态转移方程为：

\[dp_i=min\{dp_j+(time_j+s+\sum^i_{k=j+1}t_{k})*\sum^i_{k=j+1}f_k\} \]

对于 \(time_j\)，我们可以表示为：

\[time_j = \sum^j_{k=1}t_k\times f_k+num*s \]

※ \(num\) 为前 \(i\) 天做的次数。

怎么处理 \(num\) 呢？考虑到在每次做任务时，都会使当前和以后计算的时间加上 \(s\)，先不管转移方程，我们现在对未来的影响为：

\[\sum^n_{k=j+1}s\times f_k=s\times\sum^n_{k=j+1} f_k \]

于是我们可以列出一个船新的状态转移方程：

\[dp_i=min\{dp_j+\sum^i_{k=1}t_k\times\sum^i_{l=j+1}f_l+s\times\sum^n_{k=j+1} f_k\} \]

因为我们在过去已经计算了影响现在的值，所以我们只需要计算 \(\sum^i_{k=1}t_k\)。以上的各种 \(\sum\) 均可以用前缀和优化为 \(O(1)\) 的，所以时间复杂度为 \(O(n^2)\)。

数位DP

数位DP主要解决的是有关每个数位上的数字的一些关系，这种DP比较容易辨认，大多是一眼题，形如：

求 \(l\) 到 \(r(1\le l,r\le 10^{18})\) 中满足以下性质的数的个数：

每个数位.........

我们可以使用类似前缀和的思想，设 \(dp(i)\) 为 \(1\) 到 \(i\) 一共满足性质的数的个数，答案即为 \(dp(r) - dp(l-1)\)。

发现可以对于一个已经固定最高位了的任意满足条件的 \(k\) 位数的数量进行预处理，但是这个做法会假掉，原因：先设原数等于 \(\overline{kabcd\cdots e}\)（\(x\) 位数），则我们在处理满足性质的最高位为 \(k\) 的 \(x\) 位数的个数可能会包含超出原数范围的数，但是这部分的数是不可取的，并且难以维护 \(\overline{kabcd\cdots e}\) 以内的满足性质的最高位为 \(k\) 的 \(x\) 位数的个数，所以做法假了。

注意到最高位小于 \(k\) 时，我们是可以使用上文预处理的方法的，于是我们可以分类讨论：

列出以上树形图

对于左边的分支，我们可以直接用先前预处理出来的值来更新 \(ans\)，对于右边的分支，继续往下走，记录一下前面数位的情况，再针对前面的数位来进行下一位的转移。

e.g.

AcWing 1081度的数量
求给定区间 \([X,Y]\) 中满足下列条件的整数个数：这个数恰好等于 \(K\) 个互不相等的 \(B\) 的整数次幂之和。
例如，设 \(X=15,Y=20,K=2,B=2\)，则有且仅有下列三个数满足题意：
\(17=2^4+2^0\quad 18=2^4+2^1\quad 20=2^4+2^2\)