【复杂网络建模】——通过图神经网络来建模分析复杂网络-Toy模板网

这篇具有很好参考价值的文章主要介绍了【复杂网络建模】——通过图神经网络来建模分析复杂网络。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

【复杂网络建模】——通过图神经网络来建模分析复杂网络

🤵‍♂️ 个人主页：@Lingxw_w的个人主页

✍🏻作者简介：计算机科学与技术研究生在读
🐋 希望大家多多支持，我们一起进步！😄
如果文章对你有帮助的话，
欢迎评论 💬点赞👍🏻 收藏 📂加关注+

一、复杂网络介绍

二、复杂网络建模分析方法

三、基于图神经网络来建模

1、数据准备

2、构建图神经网络模型

3、学习节点和边的表示

4、特征提取和预测

5、模型评估和优化

四、可视化建模分析

1、初始网络可视化

2、特征可视化

一、复杂网络介绍

复杂网络是指由大量节点和连接组成的网络结构，它在许多领域中都有应用，包括社交网络、生物网络、信息网络等。复杂网络的研究主要关注网络的拓扑结构、动力学行为和功能特性。

复杂网络的拓扑结构通常呈现出非常复杂的特征，例如小世界效应和无标度性。小世界效应指的是网络中的节点之间具有较短的平均路径长度，使得节点之间的距离变得更短。无标度性表示网络的度分布呈幂律分布，即只有少数节点具有非常高的连接度，而大部分节点的连接度较低。这些特性使得复杂网络在信息传播、灾难传播、社交影响等方面表现出独特的性质。

在复杂网络中，节点的动态行为和交互也是研究的重点。例如，可以通过节点之间的相互作用来模拟信息传播、疾病传播等过程。此外，复杂网络还涉及到社群结构的发现和网络的演化过程的研究。

复杂网络的应用非常广泛。在社交网络中，它可以用于分析人际关系、社交影响和舆论传播。在生物网络中，复杂网络被用来研究蛋白质相互作用、神经网络等生物系统的结构和功能。在信息网络中，复杂网络被用于分析互联网拓扑结构、搜索引擎优化等领域。

二、复杂网络建模分析方法

复杂网络的建模方法有多种，下面列举几种常见的方法：

随机图模型：随机图模型是一种基于概率的建模方法，用于生成符合特定拓扑特征的复杂网络。其中最著名的是随机图模型之一的随机图模型，例如随机 Erdős-Rényi 图模型（ER 模型）和随机无标度网络模型（BA 模型）。这些模型可以通过指定节点的连接概率或生成规则来生成网络的拓扑结构。
分布式图模型：分布式图模型是一种通过节点和连接的局部规则来构建复杂网络的方法。它们通常基于节点的行为、属性或地理位置等信息来确定节点之间的连接方式。例如，小世界模型就是一种基于节点的邻居关系和随机重连机制的建模方法。
优化方法：优化方法是通过最小化或最大化某个目标函数来构建网络的方法。这些方法通常涉及到约束条件和优化算法，例如最小生成树算法、最大流最小割算法等。通过调整目标函数和约束条件，可以生成具有所需特性的网络。
基于机器学习的方法：随着机器学习的发展，越来越多的方法将机器学习技术应用于复杂网络建模。例如，可以使用监督学习或无监督学习算法来学习网络的结构和模式。另外，图神经网络是一种特殊类型的神经网络，用于处理图数据，可以用于建模和分析复杂网络。
基于现实数据的建模：这种建模方法是通过分析真实世界的数据来构建复杂网络模型。例如，可以使用社交网络中的用户关系数据或蛋白质相互作用网络的实验数据来构建网络模型。

三、基于图神经网络来建模

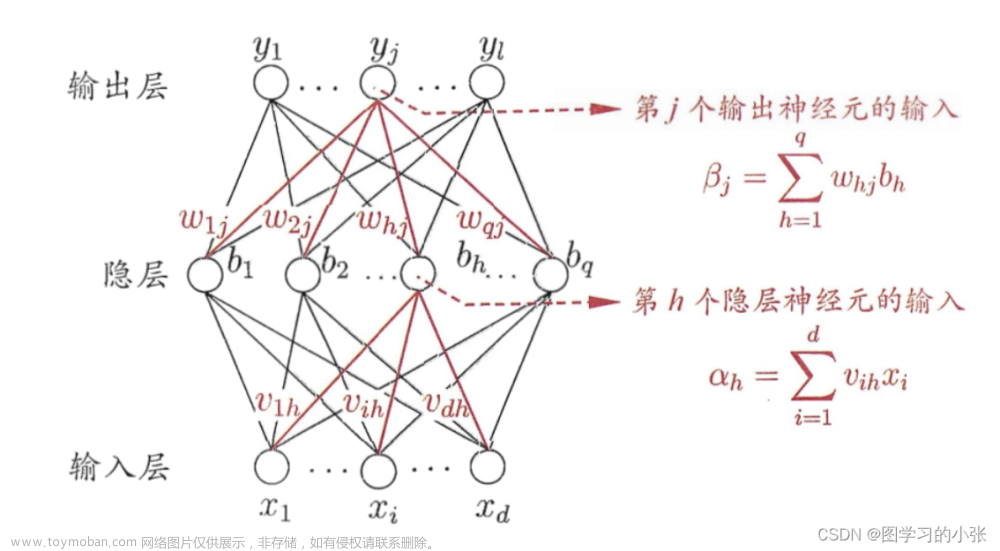
基于机器学习的方法在建模和分析网络时，通常使用图神经网络（Graph Neural Networks, GNNs）等技术来处理图数据。图神经网络是一类专门用于处理图结构数据的神经网络模型，可以学习节点和边的表示，并从图中提取特征和进行预测。

1、数据准备

首先，在提供网络数据集的网站上下载数据集。

Stanford Large Network Dataset Collection

【复杂网络建模】——通过图神经网络来建模分析复杂网络

接着，需要将网络数据转化为机器学习模型可以处理的格式。对于节点属性，可以将其表示为特征向量；对于网络结构，可以使用邻接矩阵或邻接列表表示节点之间的连接关系。

节点表示：对于每个节点，需要将其属性转化为机器学习模型可以处理的特征表示。这些属性可以是节点的数值型特征、分类型特征或文本型特征。对于数值型特征，可以直接使用原始值。对于分类型特征，可以进行独热编码或者使用嵌入向量表示。对于文本型特征，可以使用文本处理技术（如词袋模型、TF-IDF等）将其转化为向量表示。

邻接矩阵或邻接列表：网络的拓扑结构可以使用邻接矩阵或邻接列表来表示。邻接矩阵是一个方阵，其中的元素表示节点之间的连接关系。邻接列表是一个以节点为索引的列表，每个节点对应的列表包含与其相邻节点的索引。这两种表示方法可以根据具体任务和模型的需求选择适合的格式。

图特征工程：除了节点和边的表示之外，还可以进行图特征工程，从整个网络的全局特征中提取有用的信息。这些特征可以包括网络的密度、平均度、聚类系数等。可以根据任务需求和模型的要求，选择适合的图特征进行提取和处理。

标签处理：如果网络中的节点或边有标签信息，需要将其转化为机器学习模型可以处理的形式。对于分类任务，可以将标签编码为整数或进行独热编码。对于回归任务，可以直接使用数值型标签。

数据集划分：将转化后的数据划分为训练集、验证集和测试集，用于模型的训练、调优和评估。划分比例可以根据具体任务和数据集大小进行设置。

Karate Club 社交网络数据集
Karate Club 数据集是一个小型的社交网络数据集，描述了一个空手道俱乐部的成员之间的关系。数据集包含34个节点和78条边，每个节点具有0或1的标签，表示属于不同的社区。

import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

# 加载 Karate Club 数据集
edges = np.loadtxt('karate.edges')
labels = np.loadtxt('karate.labels')

# 构建正样本标签
existing_edges = edges.astype(int)
existing_labels = labels[existing_edges[:, 0]] == labels[existing_edges[:, 1]]

# 构建负样本标签（随机采样）
num_non_edges = len(existing_edges)
non_edges = []
while len(non_edges) < num_non_edges:
    node1 = np.random.randint(34)
    node2 = np.random.randint(34)
    if node1 != node2 and [node1, node2] not in existing_edges.tolist() and [node2, node1] not in existing_edges.tolist():
        non_edges.append([node1, node2])
non_edges = np.array(non_edges)
non_labels = np.zeros(num_non_edges, dtype=bool)

# 合并正样本和负样本
edges = np.concatenate([existing_edges, non_edges], axis=0)
labels = np.concatenate([existing_labels, non_labels], axis=0)

# 提取节点属性特征（这里假设每个节点没有属性特征）

# 划分训练集和测试集
train_edges, test_edges, train_labels, test_labels = train_test_split(edges, labels, test_size=0.2, random_state=42)

# 打印处理后的数据
print("训练集边：")
print(train_edges)
print("训练集标签：")
print(train_labels)
print("测试集边：")
print(test_edges)
print("测试集标签：")
print(test_labels)

我们加载了 Karate Club 社交网络数据集，包括节点之间的边和节点的标签信息。然后，我们从现有边中构建了正样本标签，即具有相同标签的节点之间的边。接下来，我们使用随机采样的方式构造了与现有边不相连的节点对，并为它们设置了负样本标签。然后，我们将正样本和负样本合并，并进行训练集和测试集的划分。最后，我们打印处理后的数据。

2、构建图神经网络模型

选择适合任务的图神经网络模型，并根据网络的特点和目标进行配置。图神经网络模型通常包含多个层，每一层都会更新节点和边的表示。

定义图结构：

创建一个空的图对象（Graph）。
添加节点到图中，节点数量为数据集中的节点数量。
添加边到图中，边的信息可以从数据集中获取。

特征表示：

如果节点具有特征属性，可以将这些特征作为节点的初始特征表示。
如果数据集中没有节点特征，可以将每个节点初始化为一个固定长度的向量作为初始特征。

构建图神经网络模型：

选择合适的图神经网络模型，例如 Graph Convolutional Networks (GCN)、GraphSAGE、GAT (Graph Attention Networks) 等。
根据模型的要求，设置模型的输入维度、隐藏层大小、激活函数等超参数。

训练图神经网络：

准备训练集和测试集，其中包括节点特征、标签和图结构信息。
将图结构和节点特征输入到图神经网络模型中，训练模型来学习节点之间的表示和关系。
通过定义损失函数（如交叉熵损失）和优化算法（如随机梯度下降），对模型进行训练。

import dgl
import torch
import torch.nn as nn
import torch.optim as optim
from dgl.nn import GraphConv

# 构建图
graph = dgl.DGLGraph()
num_nodes = 34
graph.add_nodes(num_nodes)
edges = [(int(i), int(j)) for i, j in np.loadtxt('karate.edges')]
src, dst = zip(*edges)
graph.add_edges(src, dst)

# 节点特征表示（这里假设每个节点没有特征属性，使用随机初始化的特征）
node_features = torch.randn(num_nodes, 16)

# 构建 GCN 模型
class GCN(nn.Module):
    def __init__(self, in_features, hidden_features, out_features):
        super(GCN, self).__init__()
        self.conv1 = GraphConv(in_features, hidden_features)
        self.conv2 = GraphConv(hidden_features, out_features)

    def forward(self, g, features):
        x = self.conv1(g, features)
        x = torch.relu(x)
        x = self.conv2(g, x)
        return x

model = GCN(in_features=16, hidden_features=32, out_features=2)

# 设置损失函数和优化器
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.01)

# 划分训练集和测试集
train_mask = np.random.choice([True,False], size=num_nodes, p=[0.8, 0.2])
train_idx = torch.nonzero(train_mask).squeeze()
test_idx = torch.nonzero(~train_mask).squeeze()

# 训练图神经网络模型
def train(model, graph, features, labels, train_idx, criterion, optimizer, num_epochs):
model.train()
for epoch in range(num_epochs):
optimizer.zero_grad()
output = model(graph, features)
loss = criterion(output[train_idx], labels[train_idx])
loss.backward()
optimizer.step()
if epoch % 10 == 0:
print(f"Epoch {epoch+1}/{num_epochs}, Loss: {loss.item()}")

# 执行训练
num_epochs = 100
train(model, graph, node_features, labels, train_idx, criterion, optimizer, num_epochs)

# 在测试集上评估模型
model.eval()
with torch.no_grad():
output = model(graph, node_features)
_, predicted_labels = torch.max(output[test_idx], dim=1)
accuracy = torch.eq(predicted_labels, labels[test_idx]).float().mean()
print(f"Test Accuracy: {accuracy.item()}")

3、学习节点和边的表示

通过前向传播和反向传播，使用训练数据来学习节点和边的表示。图神经网络通过聚合节点的邻居信息，并结合节点自身的特征来更新节点表示。这样，每个节点都会得到一个学习到的向量表示。

定义 GCN 模型：

在上述示例中，我们使用了两个图卷积层（GraphConv），这些层在传播过程中学习节点表示。
每个图卷积层接收图对象和节点特征作为输入，并产生更新后的节点表示作为输出。
通过激活函数（这里使用 ReLU）来引入非线性变换。

前向传播过程：

在模型的前向传播过程中，输入的节点特征和图对象被传递到第一个图卷积层。
第一个图卷积层将节点特征与其邻居节点的特征进行聚合和变换，生成更新后的节点表示。
这些更新后的节点表示被传递到第二个图卷积层，进一步聚合和变换，得到最终的节点表示。

反向传播和参数更新：

在模型的训练过程中，通过计算损失函数（这里使用交叉熵损失）来衡量模型的预测与真实标签之间的差距。
然后，使用反向传播算法计算梯度，并通过优化器（这里使用 Adam）来更新模型的参数，使损失函数最小化。
反向传播的过程将误差信号从模型的输出传递回模型的参数，从而实现参数的学习和调整。

通过多次迭代的前向传播和反向传播过程，模型逐渐学习到节点之间的关系和表示。最终，模型通过节点表示可以进行各种任务，如节点分类、链路预测等。

对于边的表示，上述示例中并未对边进行显式的表示学习。然而，通过节点的表示，我们可以利用节点表示来进行边的表示学习。例如，在链路预测任务中，我们可以使用学习到的节点表示来计算两个节点之间的相似度或连接概率，从而预测未知边的存在与否。这种方式通过节点的表示学习来间接地学习边的表示。

4、特征提取和预测

经过图神经网络的学习，可以使用学习到的节点表示来提取网络中的特征。这些特征可以用于节点分类、链接预测、图聚类、图生成等任务。例如，可以使用图神经网络模型对未标记的节点进行标签预测，或者对不存在的边进行预测。

5、模型评估和优化

对构建的图神经网络模型进行评估，使用验证集或测试集来评估模型的性能。根据评估结果，可以进行模型调优和参数优化，以提高模型的准确性和泛化能力。

# 划分训练集和测试集
train_mask = np.random.choice([True,False], size=num_nodes, p=[0.8, 0.2])
train_idx = torch.nonzero(train_mask).squeeze()
test_idx = torch.nonzero(~train_mask).squeeze()

# 训练图神经网络模型
def train(model, graph, features, labels, train_idx, criterion, optimizer, num_epochs):
model.train()
for epoch in range(num_epochs):
optimizer.zero_grad()
output = model(graph, features)
loss = criterion(output[train_idx], labels[train_idx])
loss.backward()
optimizer.step()
if epoch % 10 == 0:
print(f"Epoch {epoch+1}/{num_epochs}, Loss: {loss.item()}")

# 执行训练
num_epochs = 100
train(model, graph, node_features, labels, train_idx, criterion, optimizer, num_epochs)

# 在测试集上评估模型
model.eval()
with torch.no_grad():
output = model(graph, node_features)
_, predicted_labels = torch.max(output[test_idx], dim=1)
accuracy = torch.eq(predicted_labels, labels[test_idx]).float().mean()
print(f"Test Accuracy: {accuracy.item()}")

四、可视化建模分析

在建模和分析过程中，可视化是一个重要的步骤，它可以帮助我们更好地理解网络结构、节点特征以及模型的学习过程。以下是一些建议可视化的步骤：

1、初始网络可视化

在开始分析之前，可视化初始的网络结构，这有助于我们对网络的拓扑结构有一个直观的了解。可以使用网络可视化工具（如Gephi、Cytoscape等）来呈现节点和边的连接关系。

【复杂网络建模】——通过图神经网络来建模分析复杂网络

2、特征可视化

如果节点具有特征属性，可以通过可视化来展示节点特征的分布和变化。例如，可以使用散点图或直方图来显示节点特征的分布情况。

下面是使用热图来展示节点特征之间的相似性：

import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

# 假设有一个节点特征矩阵 features，形状为 (num_nodes, num_features)
# 假设有 10 个节点和 5 个特征
num_nodes = 10
num_features = 5

# 生成随机的节点特征矩阵
np.random.seed(0)
features = np.random.rand(num_nodes, num_features)

# 计算节点特征之间的相似性（这里使用相关系数）
correlation_matrix = np.corrcoef(features.T)

# 绘制热图
sns.heatmap(correlation_matrix, cmap='coolwarm', xticklabels=False, yticklabels=False)
plt.title('Node Feature Similarity Heatmap')
plt.xlabel('Node Index')
plt.ylabel('Node Index')
plt.show()

生成的随机矩阵：

[0.5488135 0.71518937 0.60276338 0.54488318 0.4236548 ]
[0.64589411 0.43758721 0.891773 0.96366276 0.38344152]
[0.79172504 0.52889492 0.56804456 0.92559664 0.07103606]
[0.0871293 0.0202184 0.83261985 0.77815675 0.87001215]
[0.97861834 0.79915856 0.46147936 0.78052918 0.11827443]
[0.63992102 0.14335329 0.94466892 0.52184832 0.41466194]
[0.26455561 0.77423369 0.45615033 0.56843395 0.0187898 ]
[0.6176355 0.61209572 0.616934 0.94374808 0.6818203 ]
[0.3595079 0.43703195 0.6976312 0.06022547 0.66676672]
[0.67063787 0.21038256 0.1289263 0.31542835 0.36371077]

【复杂网络建模】——通过图神经网络来建模分析复杂网络

除了上面的俩种可视化，还有下面的三种：

3、学习表示可视化

对于图神经网络模型，可视化学习到的节点表示也是很有帮助的。可以使用降维技术（如t-SNE、PCA等）将学习到的节点表示可视化在二维或三维空间中，以观察节点之间的聚类或分布情况。

4、模型性能可视化

在训练过程中，可以可视化模型的性能指标随着训练迭代次数的变化情况。例如，可以绘制训练损失和验证准确率随时间的变化曲线，以评估模型的学习进程和性能。

5、预测结果可视化

在一些任务中，如链路预测，可视化预测结果有助于我们理解模型的预测能力。可以绘制网络图，并使用不同的颜色或线条粗细表示预测为正样本或负样本的边。

关于复杂网络建模，我前面写了很多，大家可以学习参考。

【复杂网络建模】——常用绘图软件和库_图论画图软件

【复杂网络建模】——Pytmnet进行多层网络分析与可视化

【复杂网络建模】——Python通过平均度和随机概率构建ER网络

【复杂网络建模】——通过图神经网络来建模分析复杂网络

【复杂网络建模】——Python可视化重要节点识别(PageRank算法)

【复杂网络建模】——基于Pytorch构建图注意力网络模型文章来源地址https://www.toymoban.com/news/detail-449641.html

到了这里，关于【复杂网络建模】——通过图神经网络来建模分析复杂网络的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！