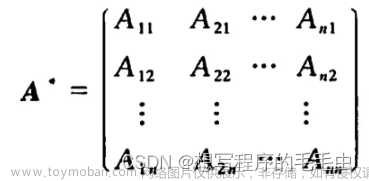
矩阵乘积的秩定理

9月前作者：dwb123456qwe 分类：Toy博客阅读(46) 违法举报

这篇具有很好参考价值的文章主要介绍了矩阵乘积的秩定理。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

矩阵乘积的秩定理

两个矩阵乘积的秩不大于其每个因子的秩；特别的当其中一个因子可逆时，那么乘积的秩等于另一个因子的秩。

证明

假设 A是一个m x n的矩阵，B是一个n x s的矩阵， r是A的秩。若 $s\lt r$ ,自然秩 $\le 秩A$ .
所以主要讨论 $s\ge r$ , 通过对A进行初等变换可以得到
$E_1E_2...E_pAE_{p+1}...E_q = \overline A = \left( \begin{array}{ccc} I_r\ \ 0\\ 0\ \ 0 \end{array} \right)$ 文章来源地址https://www.toymoban.com/news/detail-450065.html

到了这里，关于矩阵乘积的秩定理的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：

领支付宝红包赞助服务器费用

给定两个矩阵A和B，要求你计算它们的乘积矩阵AB。需要注意的是，只有规模匹配的矩阵才可以相乘。即若A有R a 行、C a 列，B有R b 行、C b 列，则只有C a

输入格式：输入先后给出两个矩阵A和B。对于每个矩阵，首先在一行中给出其行数R和列数C，随后R行，每行给出C个整数，以1个空格分隔，且行首尾没有多余的空格。输入保证两个矩阵的R和C都是正数，并且所有整数的绝对值不超过100。输出格式：若输入的两个矩阵的规模是

2024年02月12日
浏览(47)
相控阵天线（一）：直线阵列天线特性和阵列因子（方向图乘积定理、波束扫描、含python代码）

任意形式单元天线构成的直线阵如下图所示：阵中第n个单元的远区辐射场可表示为如下形式：其中An和an分别表示单元天线的激励幅度和相位，f(θ,φ)为单元天线的方向图函数。由上可得，阵列的远区总场为：化简可得阵列的方向图函数为：阵列天线的阵因子如下所示：

2023年04月10日
浏览(42)
线性代数（4）：伴随矩阵、逆矩阵和矩阵的秩

A 为一个n阶矩阵，行列式 | A | 的每个元素a ij 的代数余子式Aij组成的矩阵叫做伴随矩阵，记作 A* ； a. 如果 A 矩阵可逆，A* = | A | A^-1 b. | A | = | A |^(n-1) c. ( kA )* = k^(n-1) A* a. 若矩阵的行列式结果值不等于 0 ，那么这个矩阵就是

2024年02月08日
浏览(61)
矩阵的秩怎么求

将矩阵化为行最简矩阵，此时主元个数就是矩阵的秩。例如：矩阵 [ 1 2 − 1 3 0 0 1 5 0 0 0 0 ] begin{bmatrix} 1 2 -1 3 \\\\ 0 0 1 5 \\\\ 0 0 0 0 end{bmatrix} ⎣ ⎡ 1 0 0 2 0 0 − 1 1 0 3 5 0 ⎦ ⎤ ，第一行加上第二行，可得行最简矩阵形式，即 [ 1 2 0 8 0 0 1 5 0 0 0 0 ] begin{bmatrix} 1

2024年02月15日
浏览(53)
线性代数：矩阵的秩

矩阵的秩（Rank）是线性代数中一个非常重要的概念，表示一个矩阵的行向量或列向量的线性无关的数量，通常用 r ( A ) r(boldsymbol{A}) r ( A ) 表示。具体来说：对于一个 m × n mtimes n m × n 的实矩阵 A boldsymbol{A} A ，它的行秩 r ( A ) r(boldsymbol{A}) r ( A ) 定义为 A boldsymbol{A} A 的各

2024年02月07日
浏览(45)
矩阵的秩-

非零子式的最高阶数。如何理解？什么叫做非零子式的最高阶数？？？举个例子：有一个5阶矩阵首先什么叫子式？例如2阶子式就是，任取某两行某两列组成的行列式，就叫做子式同理，3阶子式就是任取谋三行三列组成的行列式。其次，什么叫做非零子式的最高阶数？

2024年01月23日
浏览(37)
矩阵的秩c++

最简单的理解方式，线性方程组中线性独立的方程的个数。也就是高斯消元之后，剩下的防尘组的个数，就是剩下的约束条件的个数。 cpp 代码

2024年02月12日
浏览(37)
矩阵的秩的性质

前置知识：行列式的性质逆矩阵的性质【定义】矩阵的秩线性方程组与矩阵的秩矩阵初等变换与矩阵乘法的联系前置定义 2 设在矩阵 A boldsymbol{A} A 中有一个不等于 0 0 0 的 r r r 阶子式 D D D ，且所有 r + 1 r+1 r + 1 阶子式（如果存在的话）全等于 0 0 0 ，那么 D D D 称为矩阵

2023年04月08日
浏览(81)
C语言矩阵乘积（ZZULIOJ1127:矩阵乘积）

题目描述计算两个矩阵A和B的乘积。输入第一行三个正整数m、p和n，0=m,n,p=10，表示矩阵A是m行p列，矩阵B是p行n列；接下来的m行是矩阵A的内容，每行p个整数，用空格隔开；最后的p行是矩阵B的内容，每行n个整数，用空格隔开。输出：输出乘积矩阵，输出占m行，每行n个数据

2024年02月05日
浏览(40)
矩阵乘法的秩的性质

前置定理 1 矩阵方程 A X = b boldsymbol{A} boldsymbol{X} = boldsymbol{b} A X = b 有解的充分必要条件是 R ( A ) = R ( A , B ) R(boldsymbol{A}) = R(boldsymbol{A},boldsymbol{B}) R ( A ) = R ( A , B ) 。证明见 “线性方程组与矩阵的秩”。前置性质 2 R ( A T ) = R ( A ) R(boldsymbol{A}^T) = R(boldsymbol{A}) R ( A T ) =

2024年02月03日
浏览(48)