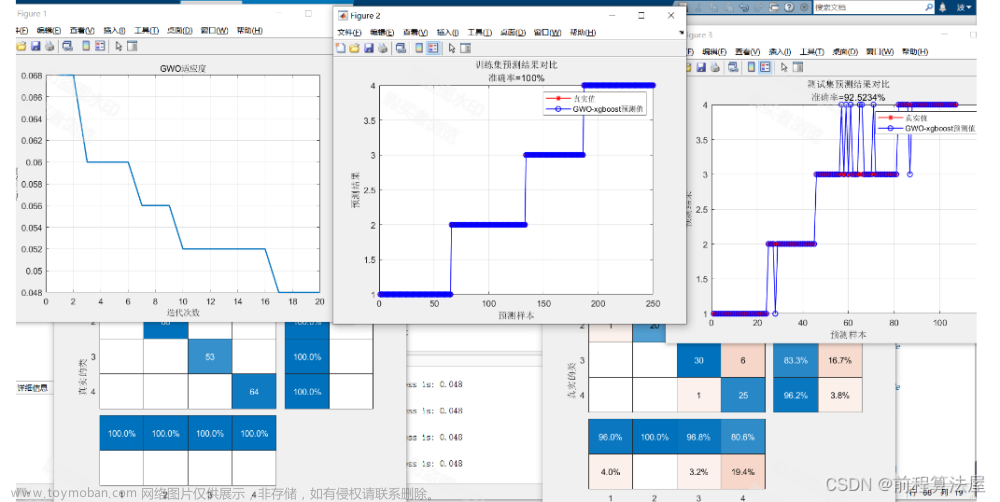
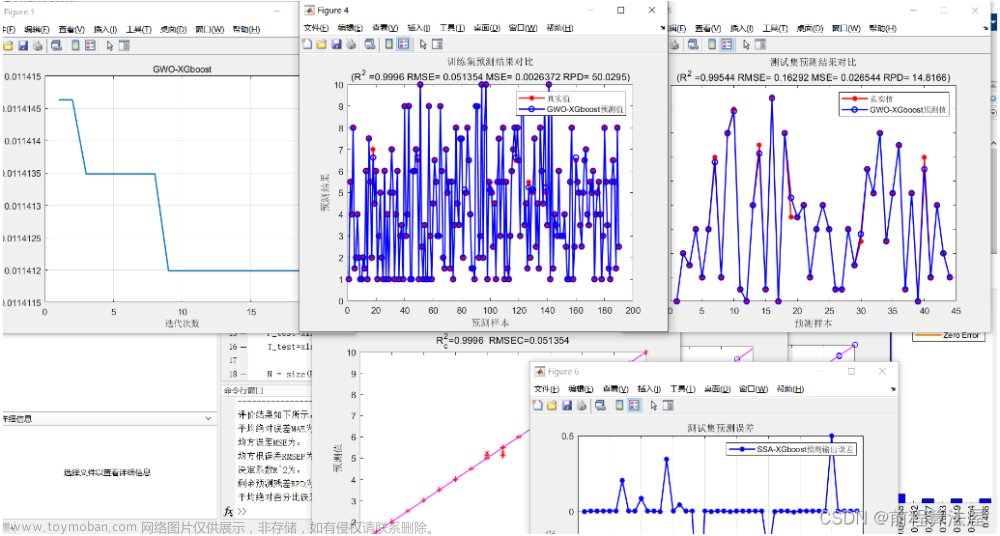
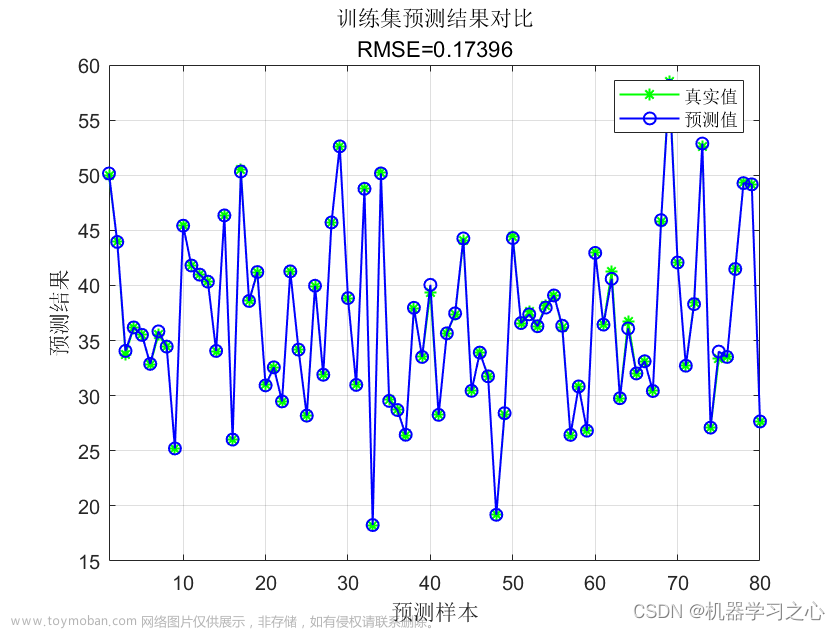
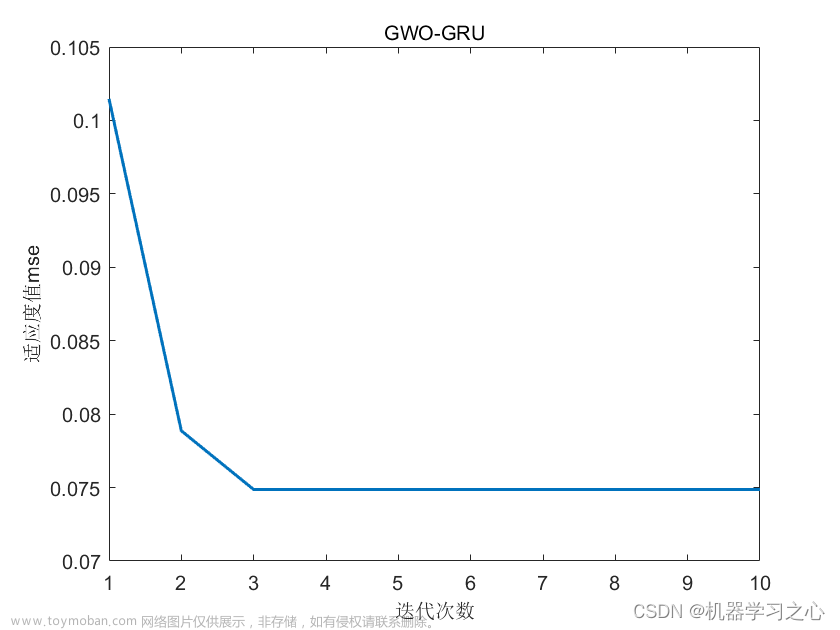
先做一个声明:文章是由我的个人公众号中的推送直接复制粘贴而来,因此对智能优化算法感兴趣的朋友,可关注我的个人公众号:启发式算法讨论。
文献[1]中的灰狼优化(Grey Wolf Optimizer, GWO)算法是2014年提出的一种群智能优化算法。严格来讲,应该叫灰狼优化器。GWO简单易实现,搜索性能较好,近年来被广泛研究。这里展示一下GWO在WOS上的引用数据,如图1所示。可以看出,这是一个被绝对高引的算法,认可度高。

图1 GWO在Web of Science上的引用数据
01 灵感来源
灰狼属于犬科动物,被认为是顶级的捕食者,它们处于生物圈食物链的顶端。灰狼大多喜欢群居,每个群体中平均有5~12只狼。特别令人感兴趣的一方面是,它们具有非常严格的社会等级制度,如图2所示。
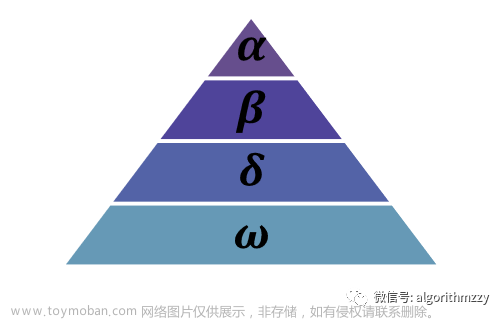
图2 灰狼群体的社会等级制度
金字塔的第一层为种群中的领导者,称为α。在狼群中α是具有管理能力的个体,主要负责关于狩猎、休息、食物分配等群体中各项需要决策的事务。金字塔的第二层被称为β。β主要负责协助α进行决策。当整个狼群的α出现空缺时,β将接替α的位置。β在狼群中的支配权仅次于α,它将α的指令下达给给其他成员,并将其他成员的执行情况反馈给α,起着桥梁作用。金字塔的第三层是δ。δ听从β的决策命令,主要负责侦查、放哨、看护等事务。适宜度不好的α和β也会降为δ。排名最低的灰狼是ω。ω扮演了替罪羊的角色。ω狼总是不得不服从于所有其他有统治力的狼。它们是最后一批被允许进食的狼。看起来ω在族群中并不是一个重要的个体,但据观察,如果失去ω,整个族群都会面临内部斗争和问题。这是由于ω是对于所有狼的暴力和挫折的发泄。这有助于满足整个族群并维持主导结构。在某些情况下,ω也是族群中的保姆,负责种群内部关系的平衡。
集体狩猎是灰狼的另一个迷人的社会行为。灰狼的社会等级在群体狩猎过程中发挥着重要的作用,捕食的过程在α的带领下完成。灰狼的狩猎包括以下3个重要部分:
1).跟踪、追逐和靠近猎物;
2).追捕、包围和干扰猎物,直到它们停止移动;
3).攻击猎物。
这些步骤如图3所示。

图3 灰狼的狩猎行为: (A) 追逐、接近和跟踪猎物 (B-D) 追逐、骚扰和包围 (E)静止状态和攻击
文献[1]对灰狼的狩猎技术和社会等级进行了数学建模,以设计灰狼狩猎策略并进行优化,从而得到了GWO算法。
02 算法设计
与往期推送一样,目前我还不会在公众号里编辑数学公式。因此,这部分内容在Word文档里先写好,然后做成图片,最后导入。

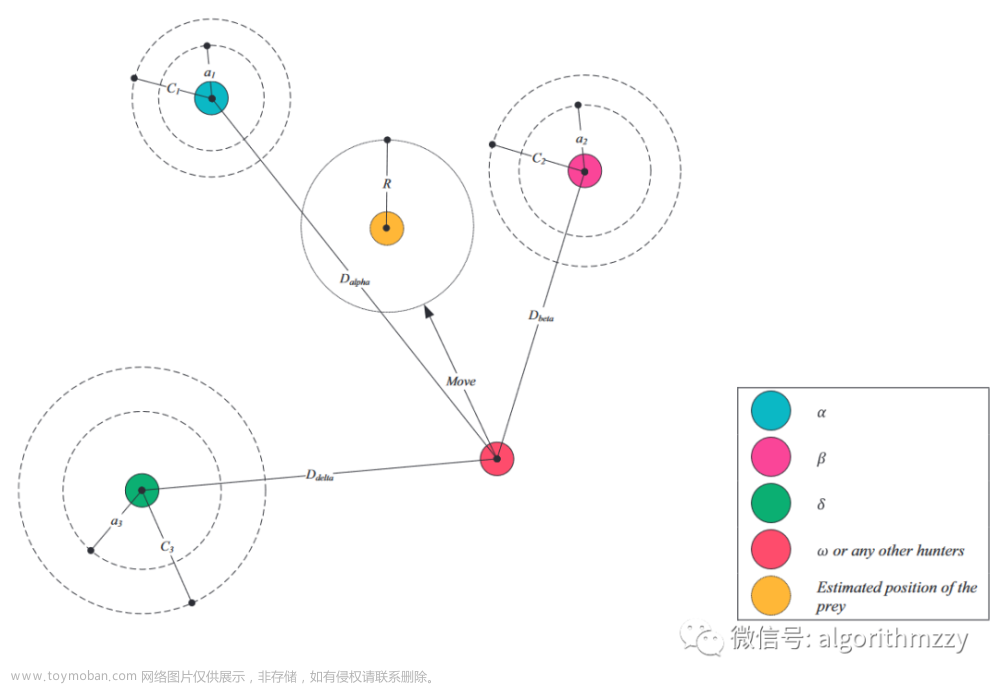
图4 灰狼位置更新示意图

03
勘探和开发的实现
勘探和开发作为进化算法的两个重要概率,在前期推送中已经详细介绍,可以点击以下链接查看:
种群的勘探(Exploration)与开发(Exploitation)(含MATLAB代码)
接下来,我们就来讨论GWO是如何全局勘探与局部开发的。
3.1 开发(攻击猎物)
如上所述,当猎物停止移动时,灰狼通过攻击猎物来完成捕猎。为了建立接近猎物的数学模型,α的值被逐渐减小。因此,A的波动范围也随之减小了。换句话说,在迭代过程中,当α的值从2线性下降到0时,其对应的A的值也在区间[-a, a] 内变化。如图5(a)所示,当A的值位于区间内时,灰狼的下一位置可以位于其当前位置和猎物位置之间的任意位置。当|A|<1时,狼群向猎物发起攻击(陷入局部最优)。
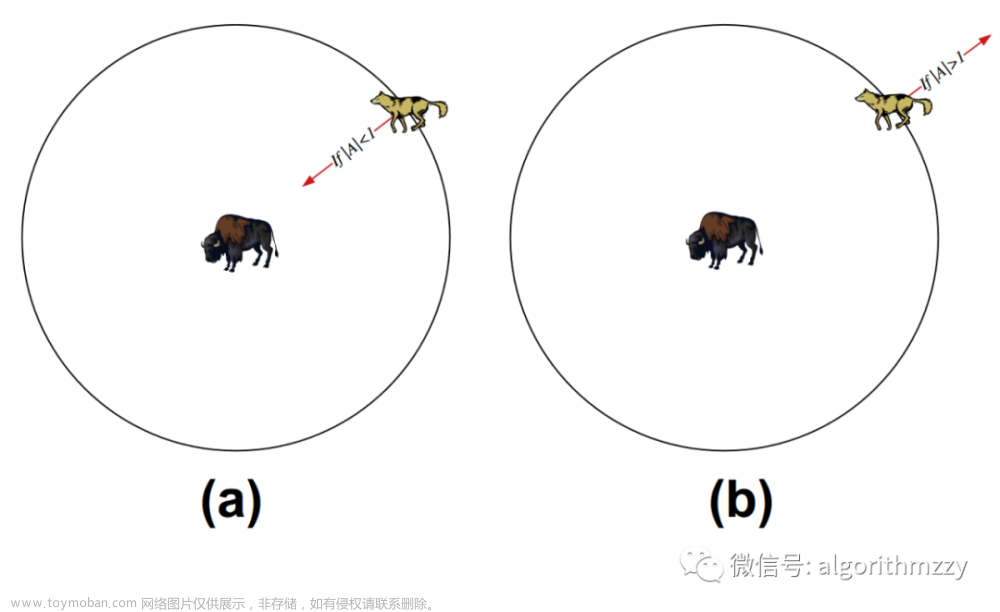
图5 攻击猎物和搜索猎物
3.2 勘探(搜索猎物)
灰狼主要根据α,β和δ狼的位置搜索猎物。它们分开去寻找猎物,聚集起来攻击猎物。为了在数学上模拟种群的分散程度,作者利用随机值大于1或小于-1的A来迫使灰狼与猎物分离。这强调了勘探,并允许GWO算法进行全局搜索。图5(b)也表明,|A|>1迫使灰狼偏离猎物(局部最优),希望找到更适合的猎物(全局最优)。GWO算法还有另一个组件C来帮助发现新的解决方案。由(4)式可知,C是[0, 2]之间的随机值。C表示灰狼所在的位置对猎物影响的随机权重:C>1表示影响权重大;反之,表示影响权重小。这有助于GWO算法更随机地进行搜索,同时可在优化过程中避免陷入局部最优。另外,与A不同,C是非线性减小的。这样,从最初的迭代到最终的迭代中,它都负责了决策空间中的全局搜索。在算法陷入局部最优并且不易跳出时,C的随机性在避免局部最优方面发挥了重要作用。
04 计算流程
GWO的实现流程图如下:
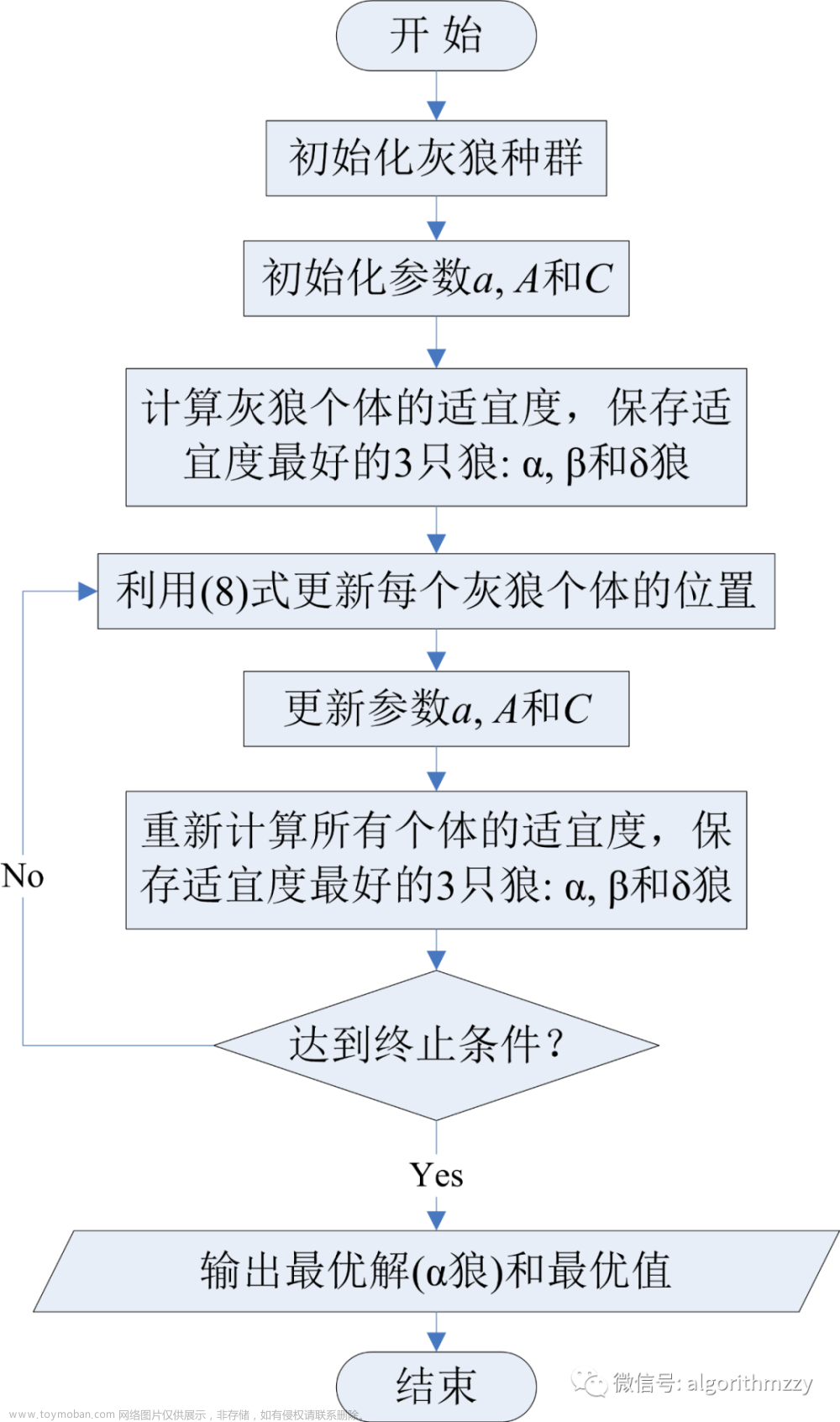
图6 GWO算法的计算流程图
05 实验仿真
这里对GWO算法的性能进行简单的测试。将GWO算法用于函数寻优,算法的MATLAB程序是严格按照它的原始参考文献进行编码的。此外,种群规模取的50,最大迭代次数为500,Benchmark函数分别采用了CEC2005测试集、CEC2013测试集、CEC2014测试集和CEC2017测试集。这里对仿真结果进行简要展示,就不再进一步做分析了。
首先,我们来检验一下GWO对全局勘探和局部开发的平衡能力。如图7所示,是GWO算法在CEC2005测试函数f8上的勘探和开发占比曲线。
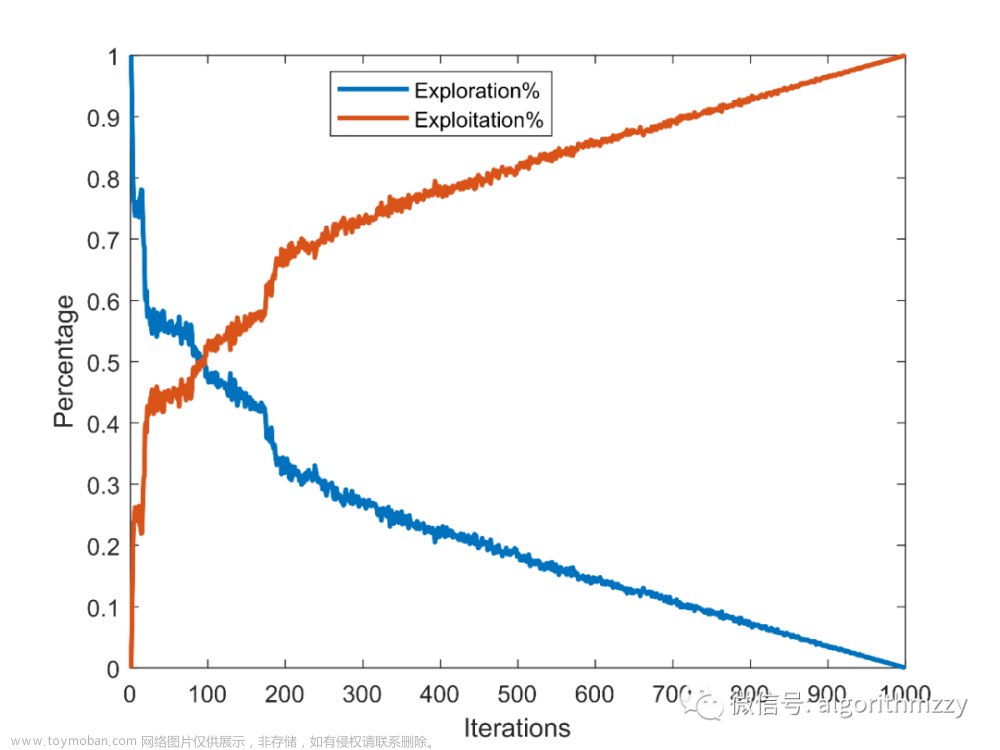
图7 GWO在CEC2005 f8上的勘探和开发百分占比变化曲线
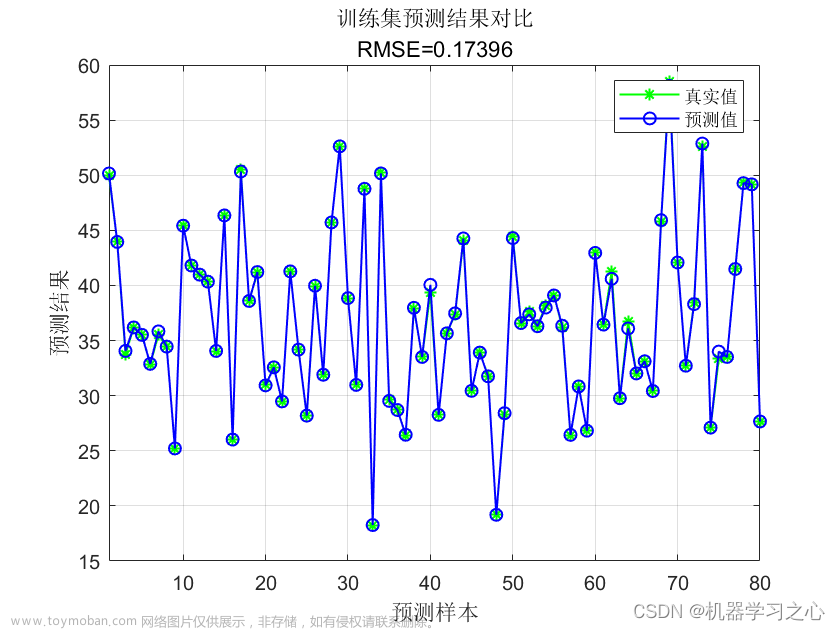
其次,以CEC2005测试集中的单峰函数Sphere (f1)和多峰函数Ackley (f10)为例,展示GWO算法在30维环境下的收敛效果,如图8所示。
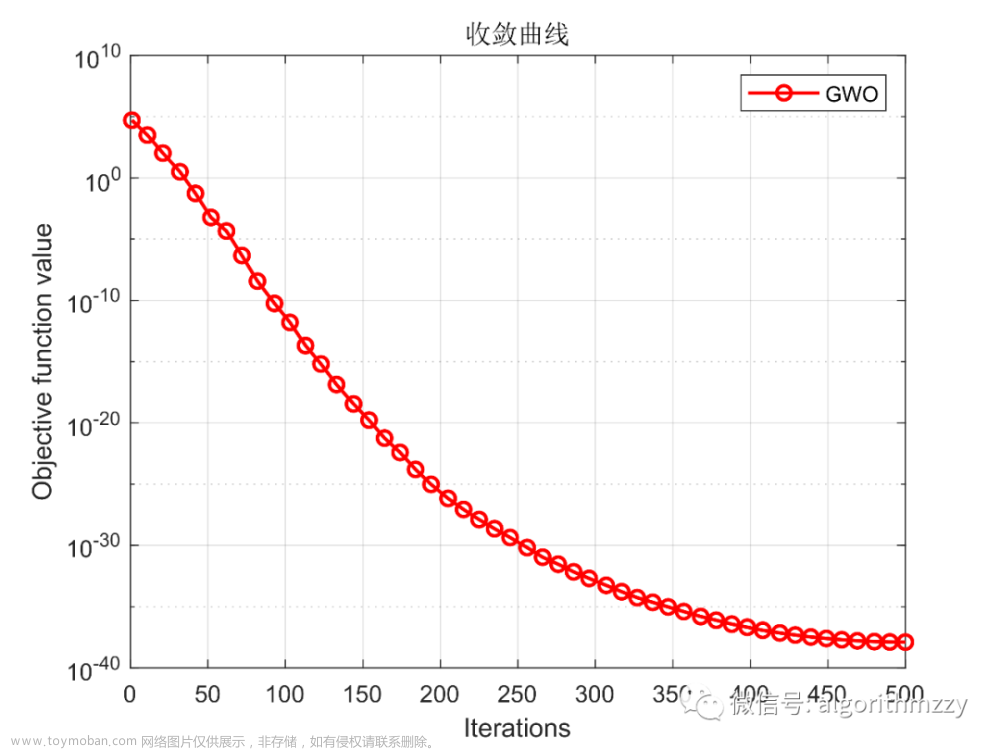
(a) 单峰函数Sphere (f1)

(b) 多峰函数Ackley (f10)
图8 GWO在CEC2005两个测试函数上的收敛曲线
再次,以CEC2013测试集中的单峰函数F1为例,展示GWO算法在30维环境下的收敛效果,如图9所示。(注意是画的误差曲线)
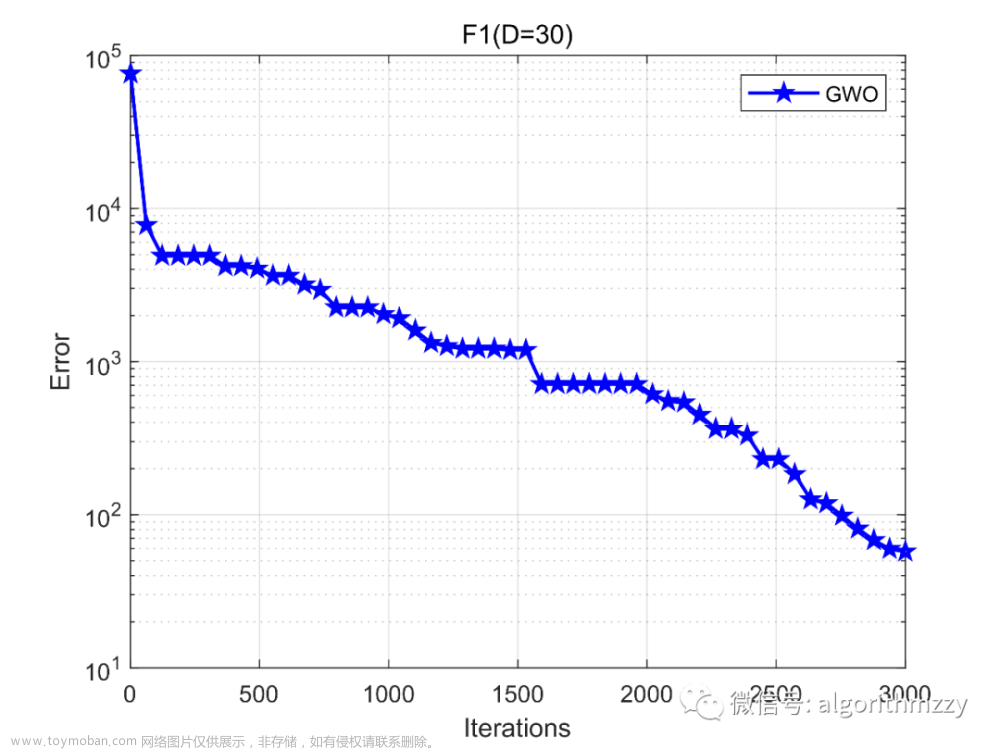
图9 GWO在CEC2013 F1上的误差收敛曲线
接着,以CEC2014测试集中的混合函数F18为例,展示GWO算法在30维环境下的收敛效果,如图10所示。(注意是画的误差曲线)

图10 GWO在CEC2014 F18上的误差收敛曲线
最后,以CEC2017测试集中的多模态函数F6为例,展示GWO算法在30维环境下的收敛效果,如图11所示。(注意是画的误差曲线)
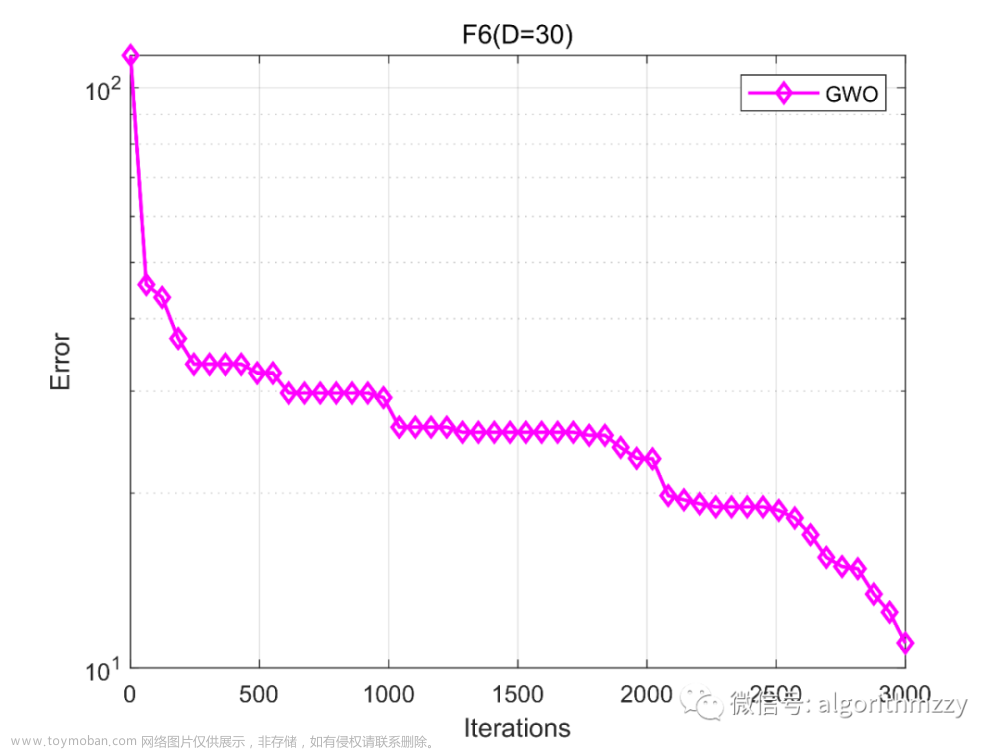
图11 GWO在CEC2017 F6上的误差收敛曲线
06 MATLAB代码
GWO算法跑CEC2005测试集:
GWO算法跑CEC2013测试集:
GWO算法跑CEC2014测试集:
GWO算法跑CEC2017测试集:
GWO算法的勘探(Exploration)和开发(Exploitation)占比分析:
(公众号里有,关注:启发式算法讨论)文章来源:https://www.toymoban.com/news/detail-450072.html
06 参考文献
[1] Mirjalili S, Mirjalili S M, Lewis A. Grey wolf optimizer[J]. Advances in engineering software, 2014, 69: 46-61.文章来源地址https://www.toymoban.com/news/detail-450072.html
到了这里,关于灰狼优化(GWO)算法(含MATLAB代码)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!