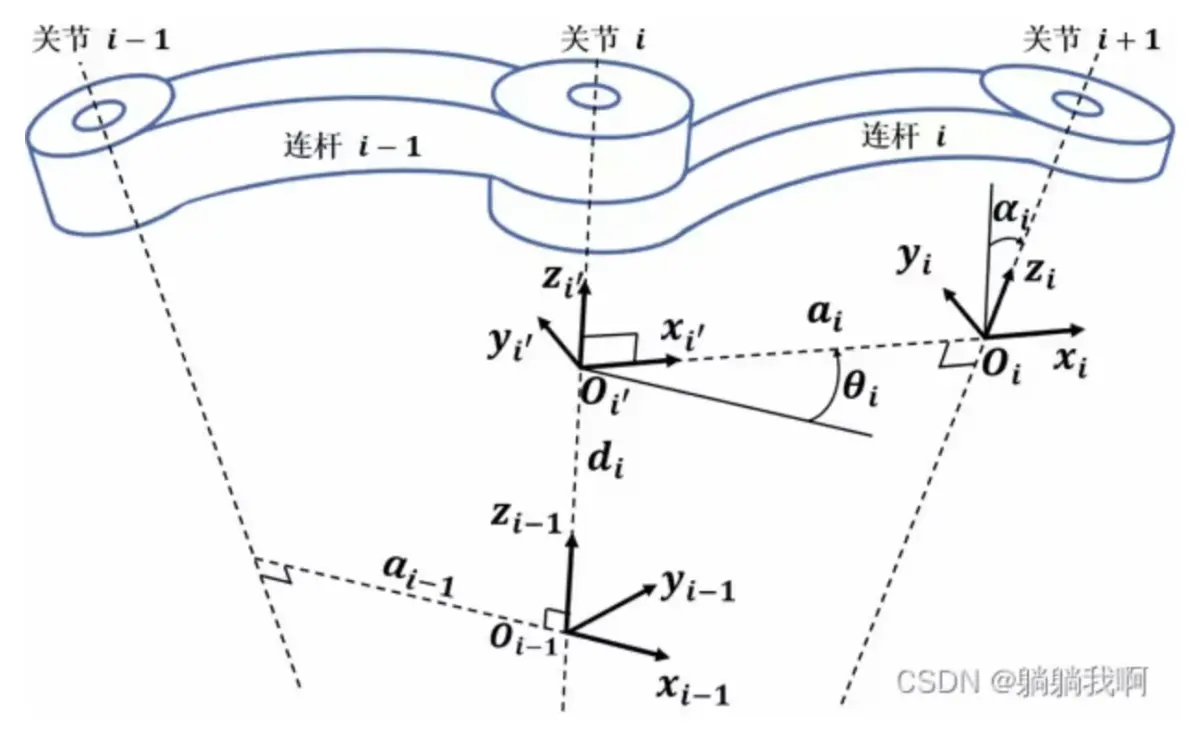
1.DH参数说明
欧几里得空间中的直角坐标系由三个两两相交且相互垂直的轴构成:X 轴,Y轴和 Z轴。因此,一个三维直角坐标系有六个变换自由度:沿 X,Y,Z 轴的平移自由度;绕 X,Y,Z 轴的旋转自由。通过这六个自由度,欧几里得空间中的直角坐标系可以完成任意线性变换,移动到任意位置。根据机器人学中的最小线性表示约定,欧几里得空间中的坐标变换,最少需要由 4 个参数描述。在众多的模型中,由 Denavit 和 Hartenberg 提出的 DH 参数模型目前运用最为广泛。
DH模型有 4 个基本参数:α:X轴旋转;a:X轴平移;θ:Z轴旋转;d:Z轴平移

DH变换参数代表着相邻坐标系之间的变换方法,通过平移旋转得到。坐标的变换满足两个定理:
定理 1:在连续变换条件下,任意平移的顺序可互换;
定理 2:在连续变换条件下,同一轴的旋转和平移顺序可互换。
故而根据X和Z轴变换顺序的不同,存在标准DH参数变换和改进DH参数变换两种方式:
标准DH参数:两个连杆坐标系变换是先绕z轴转动、平移,再绕x轴转动、平移。即X-Z顺序,先转动后平移;
改进DH参数:两个连杆坐标系变换是先绕X轴转动、平移,再绕Z轴转动、平移。即Z-X顺序,先转动后平移。
以机器人基坐标系为起始,依次转换与机器人每个关节坐标系重合,旋转关节绕Z轴旋转,根据右手法则确定方向,平移关节运动方向为(Z+)方向。
2.常用模型举例
JR603模型
a |
d |
α |
θ |
0文章来源:https://www.toymoban.com/news/detail-450474.html |
0 |
-90 |
0 |
284 |
0 |
0 |
-90 |
-30 |
0 |
90 |
180 |
0 |
286.5 |
-90 |
0 |
0 |
0 |
90 |
90 |
0 |
81.5 |
0 |
0 |
原点位置:关节(0,-90,180,0,90,0)---->空间位置(286.5,0,232.5,180,0,180)

BR606模型
a |
d |
α |
θ |
0 |
0 |
-90 |
0 |
726 |
-222.5 |
0 |
-90 |
0 |
0 |
-90 |
0 |
0 |
630.5 |
90 |
0 |
0 |
-91 |
-90 |
90 |
0 |
122 |
0 |
0 |
原点位置:关节(0,-90,0,0,90,0)---->空间(630.5,-313.5,604,0,0,180)

CO602模型(协作机器人)
a |
d |
α |
θ |
0 |
0 |
-90 |
0 |
425 |
221 |
0 |
-90 |
0 |
-172 |
90 |
180 |
0 |
375 |
-90 |
0 |
0 |
160.5 |
90 |
90 |
0 |
161.5 |
0 |
0 |
原点位置:关节(0,-90,180,0,90,0)---->空间(375,209.5,263.5,180,0,180)

5110码垛机器人
a |
d |
α |
θ |
350 |
0 |
-90 |
0 |
1100 |
-249 |
0 |
-90 |
1000 |
-248.5 |
0 |
90 |
200 |
-204 |
-90 |
0 |
0 |
169 |
0 |
0 |
0 |
0 |
0 |
0 |
原点位置:关节(0,-90,90,0,0)---->空间(1550,-701.5,931,0,0,180)文章来源地址https://www.toymoban.com/news/detail-450474.html

到了这里,关于浅谈DH参数(以华数机器人为例)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!