高斯列主元素消去法是由高斯消去法改进的算法
下面浅浅分享一下本人对该方法的理解
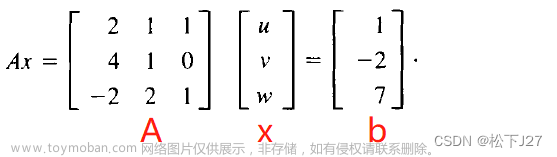
Ax = b
先说高斯消去法,感觉基本的思路就跟我们手算非齐次线性方程组差不多,在线性代数中,我们求解方程组都是这种思路,消元的过程相当于是,由系数矩阵A和非齐次项b得到的增广矩阵做行变换,化为行阶梯型,最后在由下往上回代,求出每一个未知数的过程。
举例如下所示:
由系数矩阵和非齐次项拼成的增广矩阵如下所示
我们作初等行变化将其化为行阶梯型如下
文章来源地址https://www.toymoban.com/news/detail-450772.html
到上一步之后我们就完成了消元的过程
解出未知数一步步回代就可以得到解向量如下
当然在数学上,这样的非线性方程组要有解,必须要求系数矩阵的秩等于增广矩阵的秩,不过数学上的东西就不在本篇讨论范围内了。
上面叙述的步骤在计算机程序中是很容易实现的,但考虑下面的矩阵消元。
可以看到,问题就在于,第一行第一列的元素为0,是无法消去它下方的任何数在,在计算机中也会因为0作除数而无法求解。而且就算这样的主对角线上的元素不为0,但如果元素很小的话,就会因为它是除数,而引起其他元素数量级及舍入误差的急剧增大,从而导致计算结果不可靠。
这种情况下,就产生了列主元素消去法,它的基本思想是在每步消元时,在第k列主对角线元素及其下方的元素中选取绝对值最大的元素作为主元,进行该步的消去。即体现为一个行列互换。
以上面的矩阵距离,我们用列主元素消去法逐步化简,你便会明白具体的操作步骤。
我们先将第一行第一列的元素0与它下方列所有的元素作比较,即比较0,1,2三个元素,找出他们中绝对值最大的元素,即2,我们就以2作为主元进行消去步骤,即将第①行与第③行互换,得
然后用2将下方的元素消为0,得
下面是第二行第二列的元素的消去,即3.5,与其下方的元素作比较,注意是下方元素,即不包括3,只有3.5与-3,进行绝对值比较,3.5已经是绝对值最大的元素了,所以不需要行变换,就以3.5做主元进行消去。
依次循环上面的步骤,直到完成全部主元的消去,之后便是和高斯消去法一样的回代求解过程了。
可以看出高斯列主元素消去法的思想是很简单但却十分有效的。
——————————————————————————————
下面给出我用C语言实现的代码,主要函数为EMCP()函数,大家可根据需要自行修改或使用
#include <stdio.h>
#include <stdlib.h>
/*
————————————————
说明:
————————————————
高斯列主消元法主函数为 EMCP()
函数原型为:
Double * EMCP(void * mat,double * vec)
具体用法见main()函数
使用时将main函数前的所有函数复制到自己程序的main函数前面
根据main中说明的使用方法使用本函数
复制时 所有前置函数 缺一不可,且顺序不可随意调换
最后一个PrintMat()是用来打印二维数组的,可要可不要
————————————————
@猿力觉醒
*/
//前置函数 绝对值函数
double _Abs(double value){
if(value < 0)
return -value;
else{
return value;
}
}
//前置函数 获取矩阵对应元素地址
double * _Get(void * mat,int i,int j,int N){
return ((double*)mat + i*N) + j;
}
//前置函数 行变换 交换矩阵的第a行与第b行
void _MatSwap(void * mat,int a,int b,int N){
double temp;
for(int i=0;i<N;i++){
temp = *_Get(mat,a,i,N);
*_Get(mat,a,i,N) = *_Get(mat,b,i,N);
*_Get(mat,b,i,N) = temp;
}
}
void _VecSwap(double * vec,int a,int b,int N){
double temp;
temp = vec[a];
vec[a] = vec[b];
vec[b] = temp;
}
void _Swap(void * mat,double * vec,int a,int b,int N){
_MatSwap(mat,a,b,N);
_VecSwap(vec,a,b,N);
}
//前置函数 行变换 将矩阵的第a行的k倍加到第b行
void _MatIk2J(void * mat,int a,double k,int b,int N){
double temp;
for(int i=0;i<N;i++){
temp = *_Get(mat,a,i,N) * k;
*_Get(mat,b,i,N) += temp;
}
}
void _VecIk2J(double * vec,int a,double k,int b,int N){
double temp;
temp = k * vec[a];
vec[b] += temp;
}
void _Ik2J(void * mat,double * vec,int a,double k,int b,int N){
_MatIk2J(mat,a,k,b,N);
_VecIk2J(vec,a,k,b,N);
}
//高斯列主消元法 函数主体
double * EMCP(void * mat,double * vec,int N){
//消元
for(int i=0;i<N-1;i++){
//寻找列主元
int maxEle = i;//列主元索引
for(int k=i+1;k<N;k++){
if(_Abs(*_Get(mat,k,i,N)) > _Abs(*_Get(mat,maxEle,i,N)))
maxEle = k;
}
if(*_Get(mat,i,i,N) == 0.0)
return NULL;//某列主元为0,方程无解,返回NULL
else{
_Swap(mat,vec,maxEle,i,N);//行交换
}
for(int j=i+1;j<N;j++){
//将列主元下的元素全部消为0
_Ik2J(mat,vec,i,-((*_Get(mat,j,i,N))/(*_Get(mat,i,i,N))),j,N);
}
}
double * v_out = (double*)malloc(sizeof(double)*N);
//回代
for(int i=N-1;i>=0;i--){
//解出最下方可解的元
v_out[i] = vec[i]/(*_Get(mat,i,i,N));
//对于已经解出的元,从vec中消去该元
for(int j=i-1;j>=0;j--){
vec[j] -= v_out[i]*(*_Get(mat,j,i,N));
}
}
return v_out;
}
//打印输出矩阵
void PrintMat(void * mat,int N){
for(int i=0;i<N;i++){
for(int j=0;j<N;j++){
printf("%.2lf",*_Get(mat,i,j,N));
printf(" ");
}
printf("\n\n");
}
}
//以下为测试用main函数,示意函数使用方法
int main(void){
//求解线性方程组 Ax = b 的问题(对应有限元 Ku = F 的求解)
// mat为系数矩阵,即为 A;vec为非齐次项,即为 b
double mat[3][3] = {{1,2,3},{1,5,3},{2,3,1}};
double vec[3] = {-1,-1,-1};
// EMCP()函数会更改传入的系数矩阵mat与非齐次项vec
// 故此处为了演示用法重定义了一模一样的mat与vec
double _mat[3][3] = {{1,2,3},{1,5,3},{2,3,1}};
double _vec[3] = {-1,-1,-1};
printf("Answer of question: Ax = b\n");
printf("\n\n");
printf("A is:\n");
PrintMat(mat,3);
printf("\n");
printf("b = \n");
for(int i=0;i<3;i++){
printf("%.2lf ",vec[i]);
}
printf("\n\n");
//【关键处】
//下面的语句展示了调用EMCP的用法
// double * EMCP(mat,vec,N) 一共需要3个参数
// 第一个参数mat为系数矩阵,传入C语言中的二维数组的名字即可
// 第二个参数vec为非齐次项的列向量,传入C语言中的一维数组名字即可
// 第三个参数N为方程的阶数
//
// 使用时必须保证mat与vec维数一致
double * v_out = EMCP(_mat,_vec,3);
//EMCP()返回一个双精度一维数组
// 即解向量数组
// 上面 v_out 与一维数组等价
// 可以使用如 v_out[i] 的形式访问每个元素
//
PrintMat(_mat,3);
if(v_out){
printf("Output Vector x:\n");
for(int i=0;i<3;i++){
printf("%.5lf ",v_out[i]);
}
printf("\n\n");
printf("As the following equaltion:\n");
for(int i=0;i<3;i++){
printf("|");
for(int j=0;j<3;j++){
printf("%+4.2lf ",*_Get(mat,i,j,3));
}
printf("\b\b| [%+8.5lf] = |%+4.2lf|",v_out[i],vec[i]);
printf("\n");
}
}
else{
printf("No Solution!");
}
}
文章来源:https://www.toymoban.com/news/detail-450772.html
到了这里,关于高斯列主消元法 求非齐次线性方程组 C语言实现代码的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!